Hamiltonian Definition and 833 Threads
-
P
Graduate What is Einstein's Hamiltonian for the Gravitational Field?
Hello! I have recently bought the book The Principle of Relativity by Einstein (Along with Minkowski, Lorentz and Weyl). This book is simply a collection of papers published by Einstein (along with the other three scientists mentioned) concerning the development of Special and General...- Physicist97
- Thread
- Hamiltonian
- Replies: 7
- Forum: Special and General Relativity
-

Hamiltonian of a 1D Linear Harmonic Oscillator
Homework Statement Show that for the one-dimensional linear harmonic oscillator the Hamiltonian is: [; H = \frac{1}{2}[P^2+\omega ^2 X^2]-\frac{1}{2}\omega \hbar ;] [; =\frac{1}{2}[P+i\omega X][P-i\omega X]+\frac{1}{2} \omega \hbar ;] where P, X are the momentum and position operators...- Patrick McBride
- Thread
- 1d 1d harmonic oscillator Hamiltonian Harmonic Harmonic oscillator Linear Oscillator Quantom physics
- Replies: 4
- Forum: Advanced Physics Homework Help
-
D
Graduate Relativistic Lagrangian and Hamiltonian for a free particle
Hi. I am working through a QFT book and it gives the relativistic Lagrangian for a free particle as L = -mc2/γ. This doesn't seem consistent with the classical equation L = T - V as it gives a negative kinetic energy ? If L = T - V doesn't apply relativistically then why does the Hamiltonian H =...- dyn
- Thread
- Free particle Hamiltonian Lagrangian Particle Relativistic
- Replies: 7
- Forum: Special and General Relativity
-

Graduate Commuting Hamiltonian with the projection of position
Hi all, This is the problem I want to share with you. We have the hamiltonian H=aP+bm, which we are commuting with the position x and take: [x,H]=ia, (ħ=1) Ok. Now if we take, instead of x, the operator X=Π+ x Π+ +Π-xΠ- where Π± projects on states of positive or negative energy the...- Quantum child
- Thread
- Hamiltonian Position Projection
- Replies: 7
- Forum: Quantum Physics
-
A
Hamiltonian (electron in an electro-m field)
Homework Statement Given H=\frac{1}{2m}\left[ \vec{P}-q\vec{A}\right] ^{2}+qU+\frac{q\hbar }{2m}\vec{\sigma}.\vec{B} ..(1) show that it can be written in this form; H=\frac{1}{2m}\left\{ \vec{\sigma}.\left[ \vec{P}-q\vec{A}\right] \right\}^{2}+qU ...(2) Homework Equations [/B] In my...- AhmirMalik
- Thread
- Field Hamiltonian
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Graduate Group Theory why transformations of Hamiltonian are unitary?
This is what I have so far: I'm trying to show that the matrix D has to be unitary. It is the matrix that transforms the wavefunction.- applestrudle
- Thread
- Group Group theory Hamiltonian Theory Transformations
- Replies: 2
- Forum: Linear and Abstract Algebra
-
K
Graduate What is the Quantization Scheme in Frohlich's Electron-Phonon Interaction Paper?
I am reading Frohlic's paper on electron-phonon interaction. Frohlic.http://rspa.royalsocietypublishing.org/content/royprsa/215/1122/291.full.pdf Here author has introduced the quantization for complex B field in this paper and claimed to have arrived at the diagonalized form of the...- kau
- Thread
- Electron Hamiltonian Interaction Phonon
- Replies: 12
- Forum: Atomic and Condensed Matter
-
P
Finding the Hamiltonian of this system
Homework Statement I am asked to find the Hamiltonian of a system with the following Lagrangian: ##L=\frac{m}{2}[l^2\dot\theta^2+\dot{\tilde{y}}^2+2l\dot{\tilde{y}}\dot{\theta}\sin{\theta}]-mg[\tilde{y}-l\cos{\theta}]## Homework Equations ##H = \dot{q_i}\frac{\partial L}{\partial...- pondzo
- Thread
- Hamiltonian Lagrangian System System dynamics
- Replies: 5
- Forum: Advanced Physics Homework Help
-
S
Probability for a non-hermitian hamiltonian
Homework Statement Given a non-hermitian hamiltonian with V = (Re)V -i(Im)V. By deriving the conservation of probability, it can be shown that the total probability of finding a system/particle decreases exponentially as e(-2*ImV*t)/ħ Homework Equations Schrödinger Eqn, conservation of...- shinobi20
- Thread
- Hamiltonian Non-hermitian Probability Quantum mechaincs
- Replies: 6
- Forum: Advanced Physics Homework Help
-
Graduate Hermitian Hamiltonian for KG equation
Using the Feshbach-Villars transformation, its possible to write the KG equation as two coupled equations in terms of two fields as below: ## i\partial_t \phi_1=-\frac{1}{2m} \nabla^2(\phi_1+\phi_2)+m\phi_1## ## i\partial_t \phi_2=\frac{1}{2m} \nabla^2(\phi_1+\phi_2)-m\phi_2## Then we can...- ShayanJ
- Thread
- Hamiltonian Hermitian
- Replies: 5
- Forum: High Energy, Nuclear, Particle Physics
-
G
Graduate How Fourier components of vector potential becomes operators
Hello. I'm studying quantization of electromagnetic field (to see photon!) and on the way to reach harmonic oscillator Hamiltonian as a final stage, sudden transition that the Fourier components of vector potential A become quantum operators is observed. (See...- goodphy
- Thread
- Components Electromagnetic field Fourier Fourier decomposition Hamiltonian Harmonic oscillator Operators Photon Potential Quantization Vector Vector potential
- Replies: 1
- Forum: Quantum Physics
-
A
Graduate Difference of Hydrogen Hamiltonian with relative mass particles
Hi guys, I consider the qm-derivation of the electronic states of hydrogen. There are two different derivations (I consider only the coulomb-force): 1) the proton is very heavy, so one can neglect the movement 2) the proton moves a little bit, so one uses the relative mass ##\mu## The...- Abigale
- Thread
- Difference Hamiltonian Hydrogen Hydrogen atom Mass Particles Quantum mechaincs Relative Schrodinger equation
- Replies: 2
- Forum: Quantum Physics
-

Eigenvalues of disturbed Hamiltonian
Hello everyone! I'm trying to follow a solution to a problem from the book "Problems and Solutions on Quantum Mechanics", it's problem 1017. There's a step where they go on too fast, and I can't follow. I've posted the solution and where my problem is down below. Homework Statement The dynamics...- AwesomeTrains
- Thread
- eigenfunctions eigenvalues hamiltonian quantum mechanics
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Graduate Second quantized hamiltonian change basis
Hello everyone, I m currently working on a problem that is freaking me out a bit, suppose I have a second quantized hamiltonian: \begin{eqnarray} H=H_{0}+ \epsilon d^{\dagger}d + V(d{\dagger}c_{0} + h.c) \end{eqnarray} In terms of some new operators, I would like to rotate the hamiltonian, so...- gonadas91
- Thread
- Basis Change Hamiltonian quantized
- Replies: 2
- Forum: Quantum Physics
-
R
Graduate Multiple-scale analysis for 2D Hamiltonian?
I came across a technique called "multiple-scale analysis" https://en.wikipedia.org/wiki/Multiple-scale_analysis where the equation of motion involves a small parameter and it is possible to obtain an approximate solution in the time scale of $$\epsilon t$$. I am wondering if it is possible to...- Random137
- Thread
- 2d Analysis Hamiltonian Perturbation Perturbation theory
- Replies: 45
- Forum: Beyond the Standard Models
-
M
Graduate Relation between HO and this hamiltonian
hi, i have studied the annihilation and creation operators and number operator N in relation with the simple harmonic oscillator that is governed by: H = hw(N+1/2) i don't understand the relation between the harmonic oscillator and for example, this hamiltonian: H = hw1a+a+hw2a+a+aa that i...- Matiasss
- Thread
- Hamiltonian Relation
- Replies: 1
- Forum: Quantum Physics
-

Klein-Gordon Hamiltonian commutator
Homework Statement Consider the quantum mechanical Hamiltonian ##H##. Using the commutation relations of the fields and conjugate momenta , show that if ##F## is a polynomial of the fields##\Phi## and ##\Pi## then ##[H,F]-i \partial_0 F## Homework Equations For KG we have: ##H=\frac{1}{2} \int...- loops496
- Thread
- Commutator Hamiltonian Klein gordon equation Klein gordon field Klein-gordon Quantum field theory
- Replies: 4
- Forum: Advanced Physics Homework Help
-
P
Graduate What is the relationship between dynamical symmetry and Noether's theorem?
Hi, I am learning classical mechanics right now, Particularly Noether's theorem. What I understood was that those kinds of transformations under which the the Hamiltonian framework remains unchanged, were the key to finding constants of motion. But here are my Questions: 1. What is...- phoenix95
- Thread
- Classical mechanics Groups Hamiltonian Noether's theorem Symmetry
- Replies: 9
- Forum: Beyond the Standard Models
-
H
Graduate Graphene Hamiltonian: Eq.(1) in PRB 81, 205444
As far as I know, the Hamiltonian of graphene in the Bloch's sums |A\rangle and |B\rangle near the points K or K' is a 2 \times 2 matrix with the components: \langle A|H|A\rangle, \langle A|H|B\rangle, \langle B|H|A\rangle,\langle B|H|B\rangle which all are parameters (and not variables). But in...- hokhani
- Thread
- Graphene Hamiltonian
- Replies: 1
- Forum: Atomic and Condensed Matter
-

How to solve Rashba and Dresselhaus SOC Hamiltonian
Homework Statement How can I solve this hamiltonian equation? H= p2/2m +α/ħ (σxpy - σypx) + γ/ħ (σxpx - σypy) + βxσx + βyσy Homework Equations Rashba coupling effect equation: HR=α(σykx - σxky) The Attempt at a Solution H0=ħ2k2/2m + HR+ HD- drFredkin
- Thread
- Coupling Hamiltonian Spin
- Replies: 1
- Forum: Introductory Physics Homework Help
-
L
Equation of motion from Hamiltonian
Homework Statement H=\sum^N_{i=1}(\frac{p_i^2}{2m}+\frac{1}{2}(x_{i+1}-x_i)^2+(1-\cos(2\pi x_i)) Homework Equations Hamilton equation of motion I suppose ##\dot{q}=\frac{\partial H}{\partial p}## ##\dot{p}=-\frac{\partial H}{\partial q}##[/B]The Attempt at a Solution If particles are...- LagrangeEuler
- Thread
- Equation of motion Hamiltonian Motion
- Replies: 4
- Forum: Advanced Physics Homework Help
-
K
Graduate Is there a good candidate Hamiltonian for loop QG?
is there a generally accepted candidate Hamiltonian for LQG? i've seen marcus post these papers recently http://arxiv.org/abs/1507.00986 New Hamiltonian constraint operator for loop quantum gravity Jinsong Yang, Yongge Ma (Submitted on 3 Jul 2015) A new symmetric Hamiltonian constraint...- kodama
- Thread
- Hamiltonian Loop
- Replies: 7
- Forum: Beyond the Standard Models
-
P
Graduate How to write electron hole Hamiltonian into quasi-boson?
V Chernyak, Wei Min Zhang, S Mukamel, J Chem Phys Vol. 109, 9587 (can download here http://mukamel.ps.uci.edu/publications/pdfs/347.pdf ) Eq.(2.2), Eq. (B1) Eq.(B4)-(B6). When I substitue Eq.(B4)-(B6) into Eq.(2.2), I can not recover Eq.(B1). Who can give me a reference or hint on how to write...- PRB147
- Thread
- Electron Hamiltonian Hole
- Replies: 1
- Forum: Atomic and Condensed Matter
-
P
Graduate Hamiltonian of General Relativity
Pretty straightforward question. The Einstein-Hilbert Action says that the Lagrangian for Gravity is ##L=R(-g)^{1/2}## where ##g## is the determinant of the Metric Tensor and ##R## is the Ricci Scalar (Actually I am not sure if the determinant of the metric should be included there). From this...- Physicist97
- Thread
- General General relativity Hamiltonian Relativity
- Replies: 1
- Forum: Special and General Relativity
-

Graduate Very basic question on Hamiltonian representation?
I am trying to teach myself DFT (yet again) from books and my maths is only improving at a modest pace to understand how people calculate using QM. So a very basic question now. When a Hamiltonian for a many body system is written as given in page 8 on this presentation...- askhetan
- Thread
- Hamiltonian Representation
- Replies: 7
- Forum: Quantum Physics
-
H
Graduate Hamiltonian in the position basis
According to <x|H|x\prime>=(-\hbar ^2 /2m \frac{\partial^2 }{\partial x^2}+v(x)) \delta (x-x\prime) can one draw the conclusion that the Hamiltonian is always diagonal in the position basis?- hokhani
- Thread
- Basis Hamiltonian Position
- Replies: 10
- Forum: Quantum Physics
-
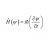
Hamiltonian for spherically symmetric potential
Homework Statement A particle of mass m moves in a "central potential" , V(r), where r denotes the radial displacement of the particle from a fixed origin. From Hamilton´s equations, obtain a "one-dimensional" equation for {\dot p_r}, in the form {{\dot p}_r} = - \frac{\partial }{{\partial...- Vitor Pimenta
- Thread
- Hamiltonian Potential Symmetric
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Undergrad Lagrangian and Hamiltonian. What are these in layman terms?
All I know is that Lagrangian is kinetic energy- potential energy and Hamiltonian is kinetic energy + Potential energy. Why do we calculate the lagrangian or hamiltonian?- avito009
- Thread
- Hamiltonian Lagrangian Layman Terms
- Replies: 2
- Forum: Beyond the Standard Models
-

Deriving the Hamiltonian of a system
Homework Statement Derive the Hamiltonian equation in terms of momentum and position ( p and r) for the given system whose lagrangian is stated as L=ř^2/(2w) - wr^2/2 Homework Equations L=ř^2/(2w) - wr^2/2 and H=př-L The Attempt at a Solution Notice here ř means first derivative of r. As i...- middleearthss
- Thread
- Classical mechanics deriving Hamiltonian System
- Replies: 2
- Forum: Introductory Physics Homework Help
-
F
Graduate Hamiltonian defined as 1st derivative
Why is Hamiltonian defined as 1st derivative with respect to time ? From the units of energy (kgm2s-2) I would expect it to be defined as 2nd derivative with respect to time. (I'm reading http://feynmanlectures.caltech.edu/III_11.html#Ch11-S2)- forcefield
- Thread
- Derivative Hamiltonian
- Replies: 10
- Forum: Quantum Physics
-

Graduate Hamiltonian Weak Gravitational Field - Learn Free Particle Theory
In weak field regime i know that it is possible to quantize the gravitational field obtaining a quantum theory of free particles, called gravitons, which is very similar to the one for the electtromagnetic field. Do you know some book in wiich i can study this theory? In anycase what is the...- Andre' Quanta
- Thread
- Field Gravitational Gravitational field Hamiltonian Weak
- Replies: 5
- Forum: Special and General Relativity
-
M
New Energy Levels for Degenerate Perturbation Theory
Homework Statement The e-states of H^0 are phi_1 = (1, 0, 0) , phi_2 = (0,1,0), phi_3 = (0,0,1) *all columns with e-values E_1, E_2 and E_3 respectively. Each are subject to the perturbation H' = beta (0 1 0 1 0 1 0 1 0) where beta is a positive constant...- ma18
- Thread
- Hamiltonian Perturbation
- Replies: 3
- Forum: Advanced Physics Homework Help
-
M
Classical Mechanics Notes needed:
Hello Seniors, I have done BSc in Physics but couldn't take lectures of Classical Mechanics. I am Almost blind in this subject. Since it's a core course in Physics, so i need your help to understand the basics in this course. If anyone of you have any helping material/notes/slides etc which...- Muhammad Toqeer
- Thread
- Classical Classical mechanics Hamiltonian Lagrange Mechanics Notes
- Replies: 1
- Forum: STEM Academic Advising
-
A
Graduate Hamiltonian for a free electron in electromagnetic field
hello, how to derive the hamiltonian for a free electron in electromagnetic field mathematically ? for a first step what is the lagrangian for a free electron in the EM field in classical mechanics ? the physics textbook always like to give the results directly.- athosanian
- Thread
- Electromagnetic Electromagnetic field Electron Field Hamiltonian
- Replies: 4
- Forum: Quantum Physics
-

Graduate Finding Wavefunction with just the Hamiltonian
Say I have a wavefunction that's a superposition of two-particle states: \Psi = \int dk ~f(k) c^{\dagger}_k c^{\dagger}_{-k} | 0 \rangle Here, ##|0\rangle## is the vacuum and ##c^{\dagger}_k c^{\dagger}_{-k} | 0 \rangle## represents a pair of fermions with momenta ##k,-k##. My goal is to solve...- metapuff
- Thread
- Hamiltonian Wavefunction
- Replies: 1
- Forum: Quantum Physics
-
W
Graduate The Role of Hamiltonian Time Dependence in Energy Conservation
Hi. Say we have found a hamiltonian ##H## for some system. So I know that if ##\frac{\partial H }{\partial t} \neq 0## then obviously the energy of the system is not conserved. But if ##\frac{\partial H }{\partial t} = 0##, is the energy always conserved? Or do we need to find that ##\frac{d H...- Wminus
- Thread
- Hamiltonian Time Time dependence
- Replies: 7
- Forum: Beyond the Standard Models
-
&
Graduate What is the physical significance of Poisson brackets?
I know the definition of the Poisson bracket and how to derive elementary results from it, but I'm struggling to understand intuitively what they are describing physically? For example, the Poisson bracket between position q_{i} and momentum coordinates p_{j} is given by \lbrace...- "Don't panic!"
- Thread
- Classical mechanics Hamiltonian Physical Poisson Poisson brackets Significance
- Replies: 3
- Forum: Beyond the Standard Models
-
A
Graduate Rovelli Quantum Gravity: Clarification on Symplectic Forms & Hamiltonian
Please refer to p. 99 and 100 of Rovelli’s Quantum Gravity book (here). I wonder what is the signification of the “naturalness” of the definition of ##\theta_0=p_idq^i##? If I take ##\theta_0'=q^idp_i## inverting the roles of the canonical variables and have the symplectic 2-forms of the...- albedo
- Thread
- Forms Hamiltonian Symplectic
- Replies: 2
- Forum: Special and General Relativity
-
R
Hamiltonian of the Half Harmonic Oscillator
Given the half harmonic potential: \begin{equation}V=\begin{cases}1/2\omega^2mx^2 & x > 0\\\infty & x < 0\end{cases}\end{equation}What will be the Hamiltonian of the half oscillator?I understand that for x>0 the Hamiltonian will be...- Raxonan
- Thread
- Hamiltonian Harmonic Harmonic oscillator Oscillator Quantum harmonic oscillator
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Graduate Lagrange and Hamiltonian formulations
Hello. Do I need to grasp well the Lagrangian and Hamiltonian formulations in classical mechanics to go through quantum mechanics without struggles?- amjad-sh
- Thread
- Hamiltonian Lagrange
- Replies: 1
- Forum: Quantum Physics
-
M
Graduate Simple Symplectic Reduction Example
Homework Statement I'm struggling to perform a symplectic reduction and don't really understand the process in general. I have a fairly solid understanding of differential equations but am just starting to explore differential geometry. Hopefully somebody will be able to walk me through this...- msparapa
- Thread
- Calculus of variations Control Example Hamiltonian Reduction Symplectic
- Replies: 3
- Forum: Differential Equations
-

Graduate Hamiltonian of an electron under EM radiation
I might have learned what I am going to ask during my electrodynamics class long time ago but just that do not remember it now. I always wonder why does an electron moving in space with EM radiation have Hamiltonian of the form ## H = \left( \mathbf{p}-e\mathbf{A}/c \right)^2/2m +e\phi## where...- blue_leaf77
- Thread
- Electron Em Em radiation Hamiltonian Radiation
- Replies: 4
- Forum: Electromagnetism
-
L
Graduate Effects of Hamiltonian Preferred Basis on Decoherence
What would be the effects on the system for different values of the Hamiltonian preferred basis in Decoherence? Would it for example make the electrons higher in orbital or bands? Or what would be the exact effects?- lucas_
- Thread
- Basis Hamiltonian
- Replies: 1
- Forum: Quantum Physics
-
T
Graduate How Are Hamiltonian and Lagrangian Related in Quantum Mechanics?
"The hamiltonian runs over the time axis while the lagrangian runs over the trajectory of the moving particle, the t'-axis." What does the above statement means? Isnt hamiltonian just an operator that corresponds to total energy of a system? How is hamiltonian related to lagrangian intuitively...- TimeRip496
- Thread
- Hamiltonian Lagrangian
- Replies: 3
- Forum: Quantum Physics
-

MHB Proving Longest Path Belongs to NP & Reducing Hamiltonian Path
Hello! (Smile) Longest path We have a graph $G=(V,E)$, lengths $l(e) \in \mathbb{Z}^{+}$ for each $e \in E$, a positive integer $K$ and two nodes $s,t \in V$. The question is if there is a simple path in $G$ from $s$ to $t$ of length at least $K$. Show that the problem Longest Path belongs...- evinda
- Thread
- Hamiltonian Path
- Replies: 19
- Forum: Programming and Computer Science
-
O
Graduate Are Constraints Necessary in Hamiltonian Dynamics?
Hi there, I'm reading on the hamiltonian method and it says we can ignore constraints? Is this true, or am I missing something here, so if we have a constraint in the system we do not have to include it in the final calculation for the equation of motion? Hope someone could clear this up, thanks!- oldspice1212
- Thread
- Constraints Hamiltonian
- Replies: 2
- Forum: Beyond the Standard Models
-
O
Graduate Hamiltonian Method: Getting Final Equation of Motion
Hey, I was hoping someone could clear this up for me. When using this method, how do you get the final equation of motion, that's where I am confused. So I know I start off using Lagrangian (T - U) -> momentum (partial L/ partial q dot) -> Hamiltonian T+U, and then using the hamiltonian...- oldspice1212
- Thread
- Hamiltonian Method
- Replies: 1
- Forum: Mechanics
-

When can I substitute transformations into the Hamiltonian?
1. If I know that ##H(q_i,p_i,t)## is a valid Hamiltonian for which the hamilton equations hold. Now we are given that ##Q_j(q_i,p_i)## and ##P_j(q_i,p_i)## are canonical transformations. This means that there is a function ##K(Q_j,P_j)##, the new hamiltonian, for which the Hamilton equations...- Coffee_
- Thread
- Hamiltonian Transformations
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Graduate Can I substitute the new coordinates in the old hamiltonian?
We went over this concept quite fast in class and there is one thing that confused me: When transforming from a set of ##q_i## and ##p_i##to ##Q_i## and ##P_i##, if one checks that the transormations are canonical the new Hamiltonian ##K(Q_i, P_i)## obeys exactly the same equations.This has...- Coffee_
- Thread
- Coordinates Hamiltonian
- Replies: 2
- Forum: Beyond the Standard Models
-
R
How Do Time-Dependent Hamiltonians Influence Quantum States?
Homework Statement I have a hamiltonian: \begin{pmatrix} a &0 \\ 0&d \end{pmatrix} + \begin{pmatrix} 0 &ce^{i w t} \\ ce^{-iwt}&0 \end{pmatrix}=\begin{bmatrix} a & c e^{i w t} \\ c e^{-i w t}&d \\ \end{bmatrix} Where the first hamiltonian can be labeled with states |1> and |2>...- rustyrusty
- Thread
- Eigenstates Hamiltonian
- Replies: 27
- Forum: Advanced Physics Homework Help