Accurate Fluid Dynamics By Video Analysis

Introduction

Providing accurate fluid dynamics experiments for undergraduate laboratories is challenging in several ways, including reproducibility, simplicity, and accessibility to introductory students.  The data from many introductory experiments, for example, is not sufficiently accurate to test whether a linear or a quadratic relationship more appropriately models the dependence of drag force on velocity.  An optimal laboratory experiment is sufficiently inexpensive for multiple groups of students to perform with accurate, repeatable results. Examples are plentiful in undergraduate kinematics laboratories, including simple harmonic oscillators and sliding block experiments.  Cost-effective and accurate experiments in fluid dynamics are less common.

Video cameras with good resolution and frame rates from 60-240 frames per second are widely available, providing an opportunity for cost-effective access to accurate experiments in fluid dynamics.  This article provides an example and explains the due care needed to ensure accurate dynamics in a laboratory experiment with common, inexpensive materials.  Simple lead and steel spheres are dropped through stacked layers of canola oil and glycerine in a clear graduated cylinder.  This design provides ample experimental data for the development and testing of predictive models with the spheres both speeding up after being released from rest in the canola oil and slowing down after transitioning from the canola to the glycerine.

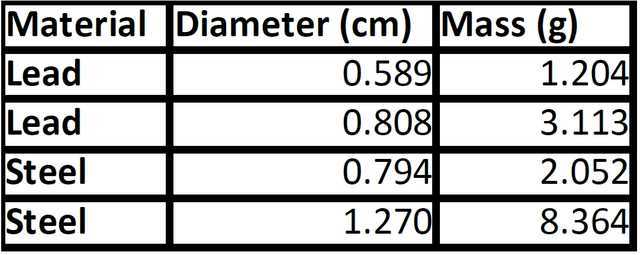
Table 1:  Diameter and mass for four spheres used in the experiment.  All digits may not be significant but are included to reduce rounding errors in anticipated predictive modeling.

Method

Four different spheres of known diameters and masses, as described in Table 1, were individually suspended using forceps near the top of a graduated cylinder containing canola oil and glycerol, then dropped to go through both fluids before reaching the bottom of the cylinder.   Liquid thicknesses were a compromise between fitting into the height of an available graduated cylinder and having smaller spheres approach terminal velocity in each liquid.  The graduated cylinder and liquids are shown in Figure 1.  Pilot testing had shown that when released from the air, an air bubble attaches to and remains with the sphere for 5-10 cm into the liquid which significantly impacts the net force and dynamics of the sphere falling through the fluid.  Releasing the sphere from a position slightly immersed in the top liquid eliminates this confounding factor and ensures more accurate data.

A video camera (Nikon CoolPix B500)  was used to record each trial at 120 frames per second and analyzed using some “best practices” as described below apply to this experiment.  Videos were then downloaded onto a computer and then imported into the free video analysis program Tracker version 5.1.1.  The raw position vs. time data was entered into a spreadsheet, and velocity vs. time was determined for each trial as described below.

Figure 1: Graduated cylinder including forceps, sphere, canola oil (golden upper liquid), and glycerine (lower liquid).  The glycerine layer is approximately 10 cm thick, and the canola layer is approximately 20 cm thick.

Over the years, our laboratory has developed some practices for ensuring greater accuracy in video analysis that was used in this experiment:

1. The camera is held in a fixed position (not handheld).  A tripod is used here.
2. The motion is kept in a single plane as equidistant as possible from the camera.  Since truly equidistant is a sphere or circle, a better approximation to equidistant is achieved by placing the camera further away so the motion subtends a smaller arc of the circle.  Here, the camera is 3 m away for vertical motion close to 30 cm.
3. The zoom feature of the camera is used to nearly fill the frame to allow as many pixels as possible to track the motion.
4. The camera is rotated to the appropriate orientation (portrait or landscape mode) so that more pixels are along the dimension of greater motion.  For vertical motion here, portrait mode was used.
5. The experiment is performed in the brightest light possible to capture motion with the fastest shutter speeds.  Here, videos were taken outside, in direct sunlight.
6. In the dimension of motion, the camera is positioned as near as possible to the center.  For the vertical motion here, the parallax of graduations on the cylinder were used to position the camera at the vertical center.
7. An appropriate and known length scale is used for calibration as near as possible to the plane of motion.  Length scales much closer or further away from the motion introduce calibration errors.  Here, the graduations on the cylinder are used for the length scale.
8. With a little practice and due care analyzing the video, the human eye is capable of determining the position of objects in each frame more accurately than the automated features in many tracking programs.  This is especially true here where resolution is limited (640 pixels) and the image is distorted by materials of varying refractive indexes between the moving object and the camera.  Stepping through and determining the object’s position manually in each frame takes a little more time (5-10 minutes per video), but yields more accurate results since the image quality present difficulties to the automated trackers.
9. Deciding whether to track the leading edge of the center of mass requires some thought.  In relatively low resolution and significantly distorted cases like the current experiment, the center of a symmetric object can be determined by the eye more reliably than the leading edge, especially since the motion is stopped effectively by the fast shutter speed ensured by full sun.  The optical distortions produce an image approximating an ellipse, and in most frames, the center of that elliptical image can be determined with an accuracy better than the height of 1 pixel.  In contrast, once slower shutter speeds result in blurs along the direction of motion, it is more reliable to use the leading edge since the size of the blurred object in each frame depends on its velocity which may be changing.
10. Tracking programs often use overly-simplified nearest neighbor algorithms to determine velocity and acceleration or use other black-box methods hidden from the user.  Here, raw position vs. time data is entered directly into a spreadsheet for further analysis.
11. Position errors on the order of 1 pixel translate to significant velocity errors when nearest neighbor positions are used as the best estimate for velocities at each frame.  More accurate velocities for each frame are determined using the idea of velocity as a “local” slope of position with respect to time.  The local slope is computed from some number of nearest neighbors usually ranging from 3-7 data points.  Here, the five nearest neighbors are used with a spreadsheet command “= slope()” as an acceptable trade-off between true instantaneous velocity and the smoothly varying velocity expected from physical considerations.
12. A range of analysis techniques produces what appears to be accurate position data, and a range of models often produces what appears to be a good visual match for position data.   Velocity data tend to provide more stringent tests both for experimental and analysis techniques, as well as for predictive models.
13. The trade-offs between frame rate and resolution require some consideration.  Pilot testing showed that the sphere would be falling for less than 0.5 seconds in each trial.  Even the highest frame rate of the camera used here (120 frames/second) would provide less than 60 data points at 640 pixels mapped over 30 cm or so for a spatial resolution close to 21 pixels per cm. Sacrificing frame rate (30 or 60 frames/second) at the expense of data points to increase the spatial resolution would not improve accuracy given the experimental design and planned analytical approach.  Comparing the data with predictive models seemed best served with at least 20 data points in each liquid.
14. When manually using the Tracker video analysis software, calibrating in cm rather than m provides more precision in the digits in the displayed position of the cursor.
15. Determining when t = 0 can be tricky.  It is difficult for inspection to identity the first frame where the object is free from its holder.  For cases such as this one where velocity increases linearly with time for the first few frames, a least squares fit for velocity vs. time is performed for the first few frames, and then the time axis is shifted in a matter that effectively defines t = 0 to be the instant where the velocity is extrapolated back to zero.  This also compensates for any accidental velocity arising from an imperfect manual release.

Predictive models require accurate fluid densities to accurately compute the buoyant forces on the falling spheres.  For the temperature at which the experiment occurred (28 °C), the densities of canola oil and glycerol were experimentally determined by measuring the mass of each fluid at 10 equal increments in a graduated cylinder on a calibrated digital scale and performing a linear least squares fit to determine density as the slope of the best fit line of mass vs. volume.  With distilled water, this technique has been shown to give agreement with accepted values to within 0.1%, which is the uncertainty in the slope performing the measurement with distilled water.  Uncertainties with canola oil and glycerine are larger, likely due to the higher viscosities of these liquids.  However, the differences between the measured densities reported here in Table 2 and typical values are significant, likely due to variations in production and purity of these consumer products. Given these variations, it is recommending that any modeling use measured densities from the experiment in question rather than typical values.

Table 2: Densities of canola oil and glycerine needed for predictive modeling.  The relative uncertainty is computed from the reported uncertainty in the best-fit slope.  The relative error is computed from the difference between typical reported densities and the measured density reported here.

 

Figure 2: Velocity vs. time for 1.204 g lead sphere.

Results

Velocity vs. time is shown in Figure 2 for the smaller lead sphere.  The data shows the expected behavior of the sphere accelerating from rest and approaching a near-terminal velocity close to 0.93 m/s as it falls through the canola oil.  As expected, the sphere begins to slow when it enters the more viscous glycerine, showing the expected behavior and slowing to a near-terminal velocity near 0.4 m/s.  To allow for potential predictive modeling, the velocity vs. time data is presented in Table 3 for the four spheres used in this experiment.  Position vs. time data is omitted to encourage modeling attempts to compare predicted and measured velocity rather than position because a wider array of models all produce an apparent agreement with the position.

1.204 g Lead		3.113 g Lead		2.052 g Steel		8.364 g Steel
time (s)	v (m/s)	time (s)	v (m/s)	time (s)	v (m/s)	time (s)	v (m/s)
0.0245	0.1548	0.0292	0.1992	0.0438	0.2424	0.0313	0.2040
0.0328	0.2172	0.0376	0.2652	0.0522	0.2964	0.0396	0.2592
0.0411	0.2820	0.0459	0.3264	0.0605	0.3492	0.0480	0.3192
0.0495	0.3348	0.0542	0.3840	0.0688	0.4020	0.0563	0.3768
0.0578	0.3888	0.0626	0.4416	0.0772	0.4476	0.0646	0.4296
0.0661	0.4404	0.0709	0.4980	0.0855	0.4848	0.0730	0.4836
0.0745	0.4884	0.0792	0.5520	0.0938	0.5280	0.0813	0.5316
0.0828	0.5388	0.0876	0.6012	0.1022	0.5700	0.0896	0.5784
0.0911	0.5748	0.0959	0.6504	0.1105	0.6072	0.0980	0.6192
0.0995	0.6144	0.1042	0.7008	0.1188	0.6504	0.1063	0.6600
0.1078	0.6552	0.1126	0.7416	0.1272	0.6768	0.1146	0.6936
0.1161	0.6900	0.1209	0.7824	0.1355	0.7068	0.1230	0.7188
0.1245	0.7212	0.1292	0.8148	0.1438	0.7356	0.1313	0.7500
0.1328	0.7428	0.1376	0.8448	0.1522	0.7524	0.1396	0.7776
0.1411	0.7668	0.1459	0.8808	0.1605	0.7764	0.1480	0.8112
0.1495	0.7908	0.1542	0.9120	0.1688	0.7896	0.1563	0.8424
0.1578	0.8160	0.1626	0.9456	0.1772	0.8088	0.1646	0.8580
0.1661	0.8364	0.1709	0.9684	0.1855	0.8304	0.1730	0.8772
0.1745	0.8532	0.1792	0.9936	0.1938	0.8460	0.1813	0.8952
0.1828	0.8724	0.1876	1.0212	0.2022	0.8604	0.1896	0.9168
0.1911	0.8832	0.1959	1.0428	0.2105	0.8616	0.1980	0.9492
0.1995	0.8916	0.2042	1.0644	0.2188	0.8664	0.2063	0.9804
0.2078	0.9012	0.2126	1.0824	0.2272	0.8724	0.2146	1.0056
0.2161	0.9048	0.2209	1.0980	0.2355	0.8892	0.2230	1.0260
0.2245	0.9168	0.2292	1.1148	0.2438	0.9024	0.2313	1.0416
0.2328	0.9216	0.2376	1.1328	0.2522	0.9252	0.2396	1.0620
0.2411	0.9228	0.2459	1.1400	0.2605	0.9420	0.2480	1.0848
0.2495	0.9300	0.2542	1.1287	0.2688	0.9396	0.2563	1.0848
0.2578	0.9288	0.2626	1.0980	0.2772	0.9408	0.2646	1.0824
0.2661	0.9312	0.2709	1.0490	0.2855	0.9230	0.2730	1.0622
0.2745	0.9211	0.2792	1.0024	0.2938	0.9134	0.2813	1.0402
0.2828	0.8875	0.2876	0.9559	0.3022	0.8894	0.2896	1.0073
0.2911	0.8280	0.2959	0.9056	0.3105	0.8327	0.2980	0.9781
0.2995	0.7560	0.3042	0.8621	0.3188	0.7765	0.3063	0.9451
0.3078	0.6854	0.3126	0.8242	0.3272	0.7140	0.3146	0.9118
0.3161	0.6308	0.3209	0.7908	0.3355	0.6684	0.3230	0.8833
0.3245	0.5892	0.3292	0.7610	0.3438	0.6451	0.3313	0.8407
0.3328	0.5508	0.3376	0.7412	0.3522	0.6089	0.3396	0.8112
0.3411	0.5311	0.3459	0.7258	0.3605	0.5827	0.3480	0.7927
0.3495	0.5069	0.3542	0.7220	0.3688	0.5598
0.3578	0.4932			0.3772	0.5269
0.3661	0.4753			0.3855	0.5190
0.3745	0.4609			0.3938	0.5036
0.3828	0.4598			0.4022	0.4861
0.3911	0.4500			0.4105	0.4775
0.3995	0.4444			0.4188	0.4596
0.4078	0.4344			0.4272	0.4566
0.4161	0.4301			0.4355	0.4462
0.4245	0.4270			0.4438	0.4499
0.4328	0.4258			0.4522	0.4487
0.4411	0.4202
0.4495	0.4164

Table 3: Velocity vs. time data for four spheres.  The data point corresponding to the first frame showing the sphere in the glycerine is shown in bold.  All digits shown may not be significant, but are shown to allow comparisons with modeling, including more accurate computations of RMS errors for different predictive models. 

Discussion

Even though this experiment was performed with a dedicated camera, many smartphones have comparable frame rates, with phones being released as early as 2012 being able to record at 120 fps with equal or higher resolution.  The accuracy of this experiment depends on due experimental care rather than expensive equipment.  The two layers of liquid allow quantitative observations of both positive and negative accelerations in each trial.  The frames after the sphere transitioned between liquids were observed carefully, and the transition appears relatively “clean” in that canola oil is not observed being dragged significantly into the glycerine.  This is in contrast to dropping spheres from the air into liquids when an air bubble attaches to and follows the sphere into the liquid and affects the motion.

Data from tracking the lead spheres was slightly more uniform than the data from tracking the shiny steel spheres.  I surmise that tracking the shiny steel spheres is more challenging under the existing optical conditions because they are reflecting light from all angles rather than providing a uniform color as the lead spheres.  It is recommended that those repeating this experiment paint or otherwise color shiny steel spheres a dark, matte color (prior to measuring diameter and mass) for more accurate tracking as the spheres fall through the liquids.

The uncertainty in the velocity determination of most data points in this experiment is between 0.5% and 2.0%, as determined from the uncertainties in the slope of the position vs. time.  One might think that greater accuracy might be obtained with some combination of higher frame rates and/or higher resolution.  However, experience has shown that once due care is exercised in video kinematics experiments as described in the method, the factor most limiting accuracy is the linearity of the mapping of pixels to distance in the light-sensing element of the camera itself.  Higher resolution and higher frame rates will not improve accuracy using a single linear calibration if the fundamental limitation is in the sensing element of the camera.  The accuracy potential of most cameras can be determined by dropping a lead sphere in the air over a distance of 0.5-0.75 m and using a least squares fit a quadratic of height vs. time to determine the acceleration of gravity.  Comparing trial variations and how the experimental value of g compares with the known value for a location suggest the accuracy potential of a given camera if due care is exercised in the experiment.  Most consumer cameras of reasonable quality provide accuracy potential from 0.5% to 2%.

Students will likely gain the most educational value by repeating an experiment substantially similar to the one described here.  Learning the due care to produce accurate data helps develop of useful laboratory skills.  However, sufficient data is also provided in this article to develop and test predictive models if a theoretical approach is preferred.  It would be instructive and useful to develop a model with the data from one trial and then use the other three trials to test the model.  For example, each fluid viscosity might be treated as an unknown, and the first trial used to determine the viscosity of each fluid by treating it as an adjustable parameter.  Then the other trials might be used to test the model by computing RMS differences between predictions and experiments using the model without any additional adjustable parameters.  Alternatively, models testing linear and quadratic dependence of drag force on velocity may be tried, using RMS differences between models and data to identify the better model (rather than visual appearance).

Comment Thread