Independent Research: Thinking Outside The Box Versus Knowing What’s In The Box

Prologue

Someone who shows interest in science is initially a welcome development. So are fresh ideas from unexpected quarters. In contrast, there is a scientific community that is meticulously organized down to the last detail, allowing little to no external influence. With the invention of social media and other sites on the internet competing for content, unprecedented opportunities have opened up for everyone to make ideas and theories accessible to a broad public. This raises the question of the boundary between the two worlds, as social media and freely accessible publication servers can hardly be compared with the reputation of well-known scientific journals. This boundary is the box. Science did not invent this term; the scientific credo actually allows for no exclusion. Rather, the term comes from the other side. Laypeople defend their ideas, and often also their lack of expertise, by urging scientists to please think outside the box. A popular rebuttal is that, conversely, one should first learn what is already in the box. The box seems to be an insurmountable hurdle, without anyone being able to say what exactly it means. We want to try to approach the box by looking at milestones in the history of science and famous open questions that have preoccupied us from ancient times to the present day.

However, the box not only has a historical dimension, but it also has a very practical one. For example, no one has an interest in reinventing the wheel, regardless of which side of the box they are on. The problem is that the wheel is inside the box, and only insiders can judge what was necessary to develop it in the first place. This is significant because it has a direct impact on the probability calculation that someone from outside the box can contribute something to its content. This, in turn, is important for calculating the effort required to evaluate such a contribution. Reviews take time, research, and often enough, a translation of unsuitable language outside the box into the language of science within the box, if not also a vivid communication about the many questions that will certainly arise during such a process of adaptation. This probability is admittedly initially a subjective probability. However, it is based on heuristics. For unsolved problems, this might include the list of those who have already attempted them, along with their reputation, the list of methods investigated, and the age of the problem. For solved problems, it is primarily the complexity of the solution. All of this data is generally only available within the box. In the past, addressing open questions often involved the development of new research methods, a process that is almost automatically linked to the contents of the box. An Éphariste Galois, who was able to independently develop a new methodology, or a Srinivasa Ramanujan, who brought an incredibly intuitive approach to number theory despite not being part of the scientific community, are the absolute exception, and by no means the rule. On the other hand, we don’t want to conceal the fact that knowledge of the contents of the box also brings with it a serious disadvantage. It obscures one’s perspective. Studying this content is laborious, time-consuming, and complicated. Therefore, there is always the danger of overlooking new paths and ideas because one is trapped within the box, the existing world of thought. However, this should not be understood as a license to assume that every thought outside the box is automatically valuable simply because of this location. So what exactly is this box, and how far outside the box were the greats of their time who contributed to the milestones in science?

Note: I will frequently quote from several Wikipedia pages without explicitly mentioning it all the time.

The Great Boxes In Physics

The narrative of the history of modern physics often begins with Isaac Newton. This is not only fraught with dubious anecdotes like the one about the apple tree, but also overshadows the findings of ancient scholars such as Archimedes, as well as those of some of his immediate predecessors, such as Galileo and Kepler. However, we have to begin somewhere, and finding out what Archimedes knew and what he didn’t know is beyond my capabilities. I’ve occasionally read that Newton said his achievements were because he stood on the shoulders of his predecessors. I don’t know if Newton actually said that, but the original quote is much older. It is from Bernard de Chartres (around 1100).

Dicebat Bernardus Carnotensis nos esse quasi nanos gigantum umeris insidentes, ut possimus plura eis et remotiora videre, non utique proprii visus acumine, aut eminentia corporis, sed quia in altum subvehimur et extollimur magnitudine gigantea.

“Bernard of Chartres said that we are like dwarfs sitting on the shoulders of giants in order to be able to see more and more distant things than them – not, of course, thanks to our own sharp eyesight or height, but because the size of the giants lifts us up.”

mentioned by John of Salisbury in Metalogicon 3,4,47–50 ca. 1159.

Issac Newton

We normally associate the origin of calculus and the laws of forces with Newton’s Principia Mathematica. But this book has around 500 pages, and Wikipedia mentions:

In this work, he combined the research of Galileo Galilei on acceleration, Johannes Kepler on planetary motion, and Descartes on the problem of inertia into a dynamic theory of gravitation and laid the foundations of classical mechanics by formulating the three fundamental laws of motion. Newton now enjoyed international recognition; young scientists who shared his unorthodox scientific (and theological) views rallied around him. Another dispute with Hooke ensued – this time over the law of gravitation. (Hooke claimed that Newton had stolen his idea that gravity decreases with the square of distance.)

The dispute about who initiated modern calculus is legendary. The English scientist Isaac Newton had already developed the principles of infinitesimal calculus in 1666. However, he did not publish his results until 1687. Decades later, this gave rise to perhaps the most famous priority dispute in the history of science. The first pamphlets accusing Leibniz and Newton of plagiarizing each other appeared in 1699 and 1704. In 1711, the dispute erupted in full force. In 1712, the Royal Society adopted a report fabricated by Newton himself; Johann I Bernoulli responded with a personal attack on Newton in 1713. The dispute continued long after Leibniz had died and poisoned relations between English and continental mathematicians for several generations. … By summing series, Leibniz arrived at integral calculus in 1675 and from there at differential calculus. He documented his observations in 1684 with a publication in the Acta Eruditorum. By today’s standards (priority of the first publication), he would be considered the sole originator of infinitesimal calculus; however, this interpretation is anachronistic, since scientific communication in the 17th century was primarily oral, through access to manuscripts and correspondence. Leibniz’s lasting achievement is, in particular, the notation of differentials (with a letter “d” from the Latin differentia), differential quotients $\tfrac{dy}{dx}$ and integrals $\int dx$; the integral symbol is derived from the letter “S” from the Latin summa.

James Clerk Maxwell

Stephen Hawking once described Maxwell’s equations as the most important discovery in physics.

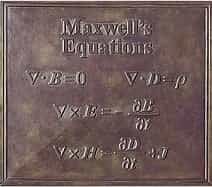
The equations are named after the Scottish physicist James Clerk Maxwell, who developed them from 1861 to 1864. He combined the magnetic field law and Gauss’s law with the induction law and, in order not to violate the continuity equation, introduced the displacement current, which is also named after him.
Gauß worked on magnetism since 1833. The Gauss-Weber telegraph was an electrical telegraph constructed in 1833 by the two German physicists Carl Friedrich Gauss (1777–1855) and Wilhelm Weber (1804–1891). Gauss’s law can be written as
$$
\nabla \cdot\vec{E}=\dfrac{\rho}{\varepsilon_0}
$$
by using the divergence theorem (Gauss, Ostrogradsky). The theorem was probably first formulated by Joseph Louis Lagrange in 1762 and later independently rediscovered by Carl Friedrich Gauss (1813), George Green (1825), and Mikhail Ostrogradsky (1831). Ostrogradsky also provided the first formal proof. The German names of Maxwell’s equations, as in the picture from the plaque on Maxwell’s statue in Edinburgh, are Gauss’s law of magnetic fields, Gauss’s law (divergence), induction law, and Ampère’s law. This is in no way meant to disparage Maxwell’s achievements, because in my opinion, his achievements lie more in the synthesis of various partial results into a larger whole than in the development of his equations from scratch. But what exactly was already known?

(1) Ampère’s law, Oersted’s law (1820), Maxwell (1855)
$$
\oint_S\vec{B}\,d\vec{s}=\mu_0I\, , \,\oint_S\vec{H}\,d\vec{s}=I
$$

(2) Faraday’s law (1831)
$$
\oint_{\partial \mathcal{A}}\vec{E}\,d\vec{s}=-\int_\mathcal{A} \dfrac{\partial \vec{B}}{dt}\,d\vec{A}
$$

(3) Gauss, Ostrogradsky (1831)

Gauss’s law for magnetism is equivalent to the statement that magnetic monopoles do not exist. This idea of the nonexistence of magnetic monopoles originated in 1269 with Petrus Peregrinus de Maricourt. His work heavily influenced William Gilbert, whose 1600 work De Magnete spread the idea further. In the early 1800s, Michael Faraday reintroduced this law, and it subsequently made its way into James Clerk Maxwell’s electromagnetic field equations.

(4) Lenz’s rule (1833)

According to Lenz’s law, a change in the magnetic flux through a conductor loop induces a voltage, so that the current flowing through it generates a magnetic field that counteracts the change in the magnetic flux, possibly combined with mechanical forces (Lorentz force).

(5) Kirchoff’s circuit laws (1845)

The algebraic sum of currents in a network of conductors meeting at a point is zero.

 

Max Karl Ernst Ludwig Planck

Planck’s paper “On the law of energy distribution in the normal spectrum” from 1900 can be seen as the origin of quantum physics.

It introduced what we nowadays call Planck’s constant as an ordinary proportion factor. In Planck’s words: Applying Wien’s displacement law (1893, ed.) in its final version to the expression of the entropy, we see that the energy element E must be proportional to the oscillation frequency $\nu$, thus
$$
E=h\cdot \nu.
$$
The German name for it is Planck’s quantum of action. However, Planck’s intention wasn’t to establish a new branch of physics. His approach was completely empirical. The more recent spectral measurements by O. Lummer and E. Pringsheim and, even more strikingly, those by H. Rubens and F. Kurlbaum, which also confirmed a result obtained earlier by H. Beckmann, have shown that the law of energy distribution in the standard spectrum, first derived by W. Wien from molecular kinetic considerations and later by me from the theory of electromagnetic radiation, does not have general validity. … The values of the two natural constants h and k (proportion factor of the entropy, ed.) can be calculated fairly accurately using the available measurements.

Hence, Planck explicitly noted that his works relied on Wien’s law and previous papers, which he all cites in footnotes.

Albert Einstein

The special relativity theory … is based on the principle of relativity formulated by Albert Einstein, according to which the principle of relativity, originally discovered by Galileo Galilei, applies not only to mechanical processes, but also to all other physical processes. According to this principle of relativity, not only the laws of mechanics, but all laws of physics have the same form with respect to every inertial system. This is especially true for the laws of electromagnetism in the form of Maxwell’s equations. It follows that the speed of light in a vacuum has the same value in every inertial system, regardless of its speed. The theory is based on this principle, and the finiteness and constancy of the speed of light. Whether this is the case has been discussed since ancient times. Empedocles (around 450 BC) already believed that light was something in motion and therefore needed time to travel distances. Aristotle, on the other hand, argued that light originates from the mere presence of objects but is not in motion. He argued that otherwise, the speed would have to be so enormous that it would be beyond human comprehension. … Foucault was the first to demonstrate the material dependence of the speed of light: light propagates more slowly in other media than in air. Foucault published his results of measuring the speed of light in 1862 and determined it to be $298,000$ kilometers per second. … Einstein’s 1905 article “On the Electrodynamics of Moving Bodies” is considered the birth of the special theory of relativity, in which he went significantly beyond the preparatory work of Hendrik Antoon Lorentz and Henri Poincaré. The main tools in Einstein’s paper from 1905 are the Lorentz transformations and the Minkowski space. The latter came shortly after Einstein, around 1907, and the former were already introduced in the ether world.
First formulations of this transformation were published by Woldemar Voigt (1887) and Hendrik Lorentz (1892, 1895), whereby these authors considered the unprimed system to be at rest in the ether, and the “moving” primed system was identified with the Earth. We must mention that Einstein explicitly derived the Lorentz transformations himself, emphasizing that the ether concept was obsolete. The paper lacks references and sources, which is a negligence from a modern point of view. He only says, “Finally, I would like to note that my friend and colleague M. Besso has been a loyal supporter to me in working on the problem discussed here, and that I owe him many valuable suggestions.”

This has changed with his paper “The Foundation of the General Relativity Theory” in 1916, in which he explicitly lists the works he based it on. “The generalization of relativity theory was greatly facilitated by Minkowski’s formulation of special relativity. Minkowski was the first mathematician to clearly recognize the formal equivalence of space and time coordinates and to use it to construct the theory. The mathematical tools necessary for general relativity were readily available in “absolute differential calculus.” This was based on the research of Gauss, Riemann, and Christoffel on non-Euclidean manifolds and had been systematically developed by Ricci and Levi-Civita and already applied to problems of theoretical physics. …Finally, I would like to thank my friend, the mathematician Grossmann, who not only saved me the trouble of studying the relevant mathematical literature, but also supported me in my search for the field equations of gravitation.” General relativity is far more difficult than special relativity and requires considerably more expertise. Its field equations alone, which can be written
$$
R_{\mu \nu}-\dfrac{1}{2}g_{\mu \nu}R=\kappa T_{\mu \nu}
$$
in their current form, at first glance, contain contradictions that can only be resolved through the study of physics. It connects geometrical properties on the left with physical properties on the right. Moreover, it speaks about curvatures and tensors in one variable: curvatures are curved and tensors are linear, i.e., straight. How can this be? The answer to this question can be found in differential geometry, a field that requires a lot of technical framework.

Amalie Emmy Noether

 

Noether’s theorem of invariant variation problems, published in 1918, is a theorem about differential equation systems and, as such, a mathematical theorem. However, its impact on physics reaches far beyond its importance in mathematics. Noether’s first theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. Noether’s second theorem is sometimes used in gauge theory. Gauge theories are the basic elements of all modern field theories of physics, such as the prevailing Standard Model. The earliest constants of motion discovered were momentum and kinetic energy, which were proposed in the 17th century by René Descartes and Gottfried Leibniz on the basis of collision experiments, and refined by subsequent researchers. Isaac Newton was the first to enunciate the conservation of momentum in its modern form and showed that it was a consequence of Newton’s laws of motion. This shows both the physical relevance of Noether’s theorems and their historical context. But what did Noether have that Newton did not have? Here is what she had to say about it:

These are variational problems that allow a continuous group (in the Lie sense); the resulting consequences for the corresponding differential equations find their most general expression in the theorems formulated in paragraph §1 and proven in the following paragraphs. … For special groups and variational problems, this combination of methods is not new; I mention Hamel and Herglotz for special finite groups, Lorentz and his students (e.g., Fokker), Weyl and Klein for special infinite groups.

Furthermore, she repeatedly mentions Lie’s work about continuous groups, today called Lie groups. Lie’s first mathematical publication, published in 1869, earned him a travel scholarship. He used this scholarship to travel to Berlin, Göttingen, and Paris, among other places. A decisive factor for Lie’s future career was his acquaintance and friendship with Felix Klein, with whom he traveled to Paris in 1870 and wrote joint papers on transformation groups. In 1872, Lie became a professor in Christiania, and in 1886, he was appointed to Leipzig, succeeding Klein (who moved to Göttingen). Noether’s paper is dedicated to Klein’s fiftieth doctoral anniversary and was presented by him as a meeting report.

The Great Boxes in the Future

The cosmological question about dark energy, the question about unifying relativity theory with quantum field theory, and the mystery of dark matter are the current great boxes in physics waiting for a satisfying treatment. How big are the chances that they can be solved by one great idea that can additionally be phrased in terms everybody can understand? Popular science magazines are full of articles about these questions. They are clickbait, in particular, as they can be described by simple means. Dark, for example, just means that we do not know, and unification already sounds like the one great idea. Let’s see what laymen have to compete with.

Engineers have built some of the biggest instruments in human history: CERN (particle physics), ALMA, FAST (radio astronomy), EHT (cosmology), SALT, ELT (optical astronomy), LIGO (gravitational waves), IceCube (neutrino detection), to name only a few. And they are productive, e.g., from the ALMA homepage:

Preliminary results after closing the Cycle 10 Call for Proposals (CfP) shows continued strong demand for ALMA time. The community submitted 1680 proposals. Although this is a slight decrease from the most recent cycles, the amount of time requested on the 12-m array increased to over 29,000 hours, which is the most time ever requested in a single cycle. This implies an overall oversubscription rate of 6.9 on the 12-meter array. The amount of time requested on the 7-m and Total Power arrays also remains very robust, with approximately 15,000 hours requested on each array.

They have output rates of more than three papers a day! This means that thousands of observations have been made, all contributing to our current knowledge of what’s in the box. It is even difficult for professionals to keep track, let alone for laypeople. Any new theory will have to explain all of them. These arguments factually take dark matter off the list, and also dark energy, as it is a hypothesis based on empirical observations on a cosmological scale. And which layperson can read the data of the Planck Surveyor? This leaves us with the grand unified theory as mainly a theoretical problem. Historically, the first true GUT, which was based on the simple Lie group $SU(5),$ was proposed by Howard Georgi and Sheldon Glashow in 1974. The Georgi-Glashow model was preceded by the semisimple Lie algebra Pati-Salam model by Abdus Salam and Jogesh Pati also in 1974, who pioneered the idea to unify gauge interactions.

The bad news is that it requires knowledge of general relativity theory, as well as of quantum field theory. One can hardly unify what isn’t profoundly understood. And we are around 50 years down the road of trying to find one.

The Great Boxes In Mathematics

In my opinion, there is no equivalent category of great boxes in mathematics. The great achievements often sneaked in silently: the quantitative treatment of Greek geometry by coordinates, analytical geometry, the consideration of the rate of changes in calculus, the concept of classes in set theory, or topology.

The term “topology” was first used around 1840 by Johann Benedict Listing; however, the older term analysis situs (roughly “investigation of location”) remained in use for a long time, with a focus beyond the newer, “set-theoretic” topology. The term topology became established in the 20th century with the book of the same name by Solomon Lefschetz (1930). Another book by Lefschetz from 1942 established the term algebraic topology instead of the previously used term “combinatorial topology”. Leonhard Euler’s solution of the Seven Bridges Problem in 1736 is considered the first topological and, at the same time, the first graph-theoretic work in the history of mathematics.

They all evolved from necessity, often enough driven by problems in physics. They represent rudimentary concepts rather than big theories, and the question of who was first usually leads to groups of mathematicians who communicated through letters or teacher-student relationships.

What might publicly be considered as big boxes, Galois’s solution to the three classical problems of Geometry (squaring the circle, doubling the cube, cutting an angle into thirds), Gödel’s incompleteness theorems, Gödel’s and Cohen’s result about the independence of the Axiom of Choice, Appel-Haken’s Four Color Theorem, Wiles’ proof of Fermat’s Last Theorem, or Perelman’s proof of the Poincaré conjecture, are mathematically only relevant for scientists working in very narrow fields. They didn’t revolutionize mathematics as Maxwell’s equations or Planck’s black body radiation law revolutionized physics. One would think that Russel’s paradox, Gödel’s incompleteness, and the logical meaning of the axiom of choice had shattered the foundations of mathematics, and, in a way, they did. But the majority of mathematicians accepted the results, shrugged their shoulders, and continued as usual.

Maybe, once we have it, the proof of the Extended Riemann Hypothesis will fulfill the requirements of a revolutionary result because it has so many consequences in related fields, not the least in cryptography. However, I think this would only be the case if it turns out to be false, which nobody really believes in, as we already tested the first ten trillion cases.

Another great question is whether the computation classes P and NP are equal or not. But this is just another very specific question, which I expect to have more philosophical implications (Are there inherently difficult problems, or are we just dumb?) than practical ones. Sure, algorithms with a polynomial runtime could improve everyday algorithms like the Traveling Salesman Problem, which we only have approximations and exponential runtime algorithms for, but this could be irrelevant if the transformation polynomial is only large enough.

Both examples of open questions, ERH and P=NP, are not suited to be solved by laymen. Even their correct phrasing already requires specific knowledge. And if we consider how long they haven’t been able to be solved by professional scientists, and it didn’t lack attempts, I’m afraid there is no naive approach.

Epilogue

It is nowadays easier than ever to publish something on the internet, be it on a homepage, on a social media website, or on servers that host specifically scientific results. I have read more than once an introduction along the lines: I am an independent researcher without an academic background/education, but I have an idea. It is indeed alluring to solve one of those problems of our times by finding the one significant idea that opens access to an approach, to become one of those names who are identified with the great revolutionary theories in physics or mathematics. However, how likely is that? We have seen that those theories didn’t evolve from nowhere in the past, and that the geniuses we nowadays relate with them had indeed profound knowledge of their fields at their time. Even if it cannot always be proven conclusively, especially if it was a long time ago, whether someone actually knew what they could have known, it can be said with some certainty that none of them were laypeople. There are many reasons why a problem has not yet been solved. However, it would be presumptuous to conclude that a simple solution is possible from the simplicity of its description; just as regrettably, it would be presumptuous to think that someone without a scientific background could discover what so many with a scientific background have not been able to discover, all the more so because the solution to one of these problems usually has implications for many other theories and observations that are often completely unknown to independent researchers.