Parallel Programming on an NVIDIA GPU

This article is the first of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different approaches to solve the same problem: finding the best-fitting line (or regression line) for a set of points.

The two different approaches to parallel programming presented in this and the following Insights article use these technologies:

• Single-instruction multiple-thread (SIMT) programming is provided on the Nvidia® family of graphics processing units (GPUs). In SIMT programming, a single instruction is executed simultaneously on hundreds of microprocessors on a graphics card.
• Single-instruction multiple data (SIMD) as provided on x64 processors from Intel® and AMD® (this article). In SIMD programming, a single instruction operates on wide registers that can contain vectors of numbers simultaneously.

The focus of this article is my attempt to exercise my computer’s Nvidia card using the GPU Computing Toolkit that Nvidia provides. The follow-on article, Parallel Programming on a CPU with AVX-512 | Physics Forums, uses Intel AVX-512 assembly instructions and includes comparison times of the results from both programs.

Introduction

Although I installed the Nvidia GPU Computing Toolkit and associated samples about five years ago, I didn’t do much with it, writing only a small number of simple programs. More recently, I decided to take another look at GPU programming, using the newer graphics card on my more powerful computer.

After I downloaded a newer version of the GPU Computing Toolkit (ver. 10.0 – newer versions exist) and got everything set up, I proceeded to build some of the many samples provided in this toolkit. I then decided to try my skill at putting together the example program that is described in this article.

Regression line calculations

Given a set of points (X_i, Y_i), where i ranges from 1 to N, the slope m and y-intercept b of the regression line can be found from the following formulas.

$$m = \frac{N \left(\sum_{i = 1}^N X_iY_i \right)~ -~  \left(\sum_{i = 1}^N X_i \right) \left(\sum_{i = 1}^N Y_i \right)}{N\left(\sum_{i = 1}^N X_i^2\right) – \left(\sum_{i = 1}^N X_i\right)^2 }$$

$$b = \frac{\sum_{i = 1}^N Y_i – \sum_{i = 1}^N X_i} N$$

As you can see from these formulas, there are a lot of calculations that must be performed. The program must calculate the sum of the x coordinates and the sum of the y coordinates. It must also calculate the sum of the squares of the x coordinates and the sum of the term-by-term xy products. For the latter two sums, it’s convenient to create two new vectors. The first vector consists of the term-by-term products of the x coordinates with themselves. The second consists of the term-by-term product of the x- and y-coordinates.

Disclaimer

Although the program I’m presenting here uses the GPU to calculate the term-by-term vector products $< X_i Y_i>$ and $<X_i^2>$ , it does not use the GPU to calculate the four sums.  It turns out that this is a more complicated problem to tackle. Although the NVidia Toolkit provides samples of summing the elements of a vector, these examples are considered advanced topics. For that reason, my code doesn’t use the GPU to calculate these sums.

Basic terms

• thread – the basic unit of computation. Each core is capable of running one thread. Threads are organized into blocks, which can be one-dimensional, two-dimensional, or three-dimensional. For this reason, a thread index, threadIdx, can have one, two, or three components, depending on how the blocks are laid out. The three components are threadIdx.x, threadIdx.y, and threadIdx.z. Thread indexes that aren’t used have default values of 1.
• block – a collection of threads. Because blocks can be organized into one-dimensional, two-dimensional, or three-dimensional arrangements, an individual block can be identified by one or more block indexes: blockIdx.x, blockIdx.y, or blockIdx.z. Block indexes that aren’t used have default values of 1. All vectors in my program are one-dimensional, so threadIdx.y, threadIdx.z, blockIdx.y, and blockIdx.z aren’t relevant. A program working with image data would likely use a two-dimensional grid, and would therefore use some of these other builtin variables.
• grid – a collection of blocks, with the blocks containing threads.

The CUDA kernel

To access the NVidia GPU architecture, a programmer uses the API provided in the NVidia GPU Toolkit to write a CUDA (Compute Unified Device Architecture) program. Such a program will contain at least one CUDA kernel, NVidia’s term for a per-thread function that runs on one of the GPU’s cores. For the kernel shown below, each core will multiply the i-th elements of two vectors, and store the result in the corresponding element of a third vector. The NVidia GPU I’m running has 1,024 cores, it should make short work of multiplying the elements of two vectors of fairly high dimension.

__global__ void
vectorMult(double *C, const double * A, const double * B, int numElements)
{
    int i = blockDim.x * blockIdx.x + threadIdx.x;
    if (i < numElements)
    {
        C[i] = A[i] * B[i];
    }
}

When this kernel runs, each of potentially 1,024 streaming multiprocessors (SMs) multiplies the values from two input vectors, and stores the product as an output value in a third vector. Figure 1 shows these actions.

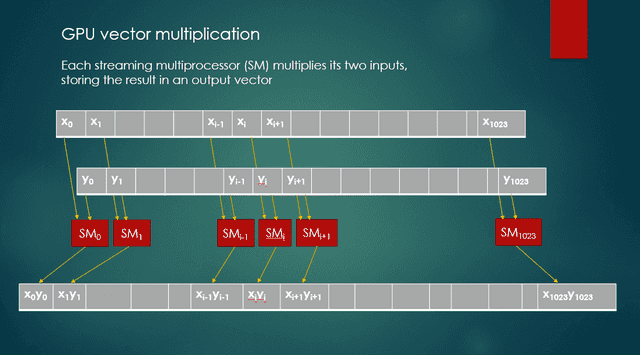
Fig. 1 GPU vector multiplication

vectorMult kernel details

The __global__ keyword is a CUDA extension that indicates a function is a kernel, and is intended to run on the GPU. A kernel function’s return type must be void.

The function header indicates that this function takes four parameters. In order, these parameters are:

• a pointer to the output vector,
• a pointer to the first input vector,
• a pointer to the second input vector,
• the number of elements in each of the three vectors.

The variable i establishes the connection between a specific thread and the corresponding index of the two input vectors and the output vector. For this connection, the program has to identify a specific block within the grid, as well as the thread within that block. For my program, each input vector contains 262,144 double values. This number happens to be 512 X 512, or $2^{18}$.  If I choose a block size of  256 (meaning 256 threads per block), there will be 1024 blocks in the grid. A block size of 256 in a one-dimensional arrangement means that blockDim.x is 256.

As an example in the code sample above, to access thread 2, in block 3, blockDim.x is 256, blockIdx.x is 3, and threadIdx.x is 2. In Figure 2, block 3 and thread 2 are shown. The index for the input and output vectors is calculated as 256 * 3 + 2, or 770. Thread 2 of block 3 is the $770^{th}$ thread of the grid. Keep in mind that a GPU can perform hundreds of these types of per-thread computations simultaneously.

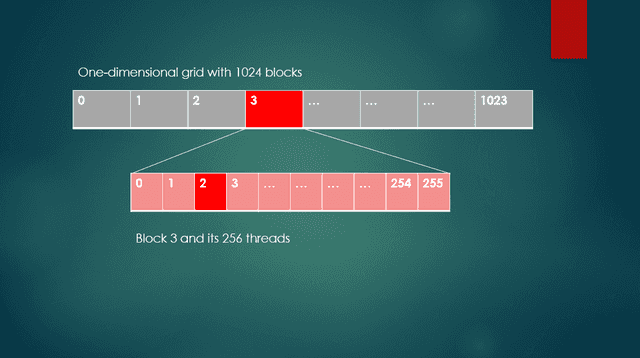
Fig. 2 One dimensional grid with a block and threads

The CUDA program

To use the capabilities of a GPU, a program must perform the following steps.

1. Allocate memory on the host.
2. Initialize input vector data.
3. Allocate memory on the device.
4. Copy data from the host to the device.
5. Set up parameters for a call to the kernel, including the number of blocks in the grid, and the number of threads per block, as well as the parameters of the kernel function itself.
6. Call the kernel.
7. Copy output data from the device back to the host.
8. Free device memory and host memory.

Each of these steps is discussed in the next sections.

Allocate host memory

The program allocates memory on the host by using the C standard library function, malloc. This should be familiar to anyone with experience in C programming. Throughout the code, an h_ prefix denotes a variable in host memory; a d_ prefix denotes a variable in device memory on the GPU.

int numElements = 512 * 512; // = 262144, or 2^18
size_t size = numElements * sizeof(double);

double *h_X = (double *)malloc(size);
double *h_Y = (double *)malloc(size);
double *h_XY = (double *)malloc(size);
double *h_XX = (double *)malloc(size);

Initialize input data

For the sake of simplicity as well as a check on program accuracy, the data in the input vectors are points that all lie on the line $y = 1.0x + 0.5$. The loop below initializes the h_X and h_Y vectors with the coordinates of these points. The loop below is “unrolled” with each loop iteration generating four sets of points on the line.

const double slope = 1.0;
const double y_int = 0.5;

// Fill the host-side vectors h_X and h_Y with data points.
for (int i = 0; i < numElements; i += 4)
{
    h_X[i] = slope * i;
    h_Y[i] = h_X[i] + y_int;
    h_X[i + 1] = slope * i;
    h_Y[i + 1] = h_X[i + 1] + y_int;
    h_X[i + 2] = slope * (i + 2);
    h_Y[i + 2] = h_X[i + 2] + y_int;
    h_X[i + 3] = slope * (i + 3);
    h_Y[i + 3] = h_X[i + 3] + y_int;
}

Allocate device memory

The program allocates memory on the device by using the CUDA cudaMalloc function. The first parameter of cudaMalloc is a pointer to a pointer to the type of element in the vector, cast as type void**. The second parameter is the number of bytes to allocate. The cudaMalloc function returns cudaSuccess if memory was successfully allocated. Any other return value indicates that an error occurred.

double *d_X = NULL;
err = cudaMalloc((void **)&d_X, size);

The code for allocating memory for d_Y is nearly identical.

Copy data from host to device

To copy data from host (CPU) to device (GPU) or from device to host, use the CUDA cudaMemcpy function. The first parameter is a pointer to the destination vector, and the second parameter is a pointer to the source vector. The third parameter is the number of bytes to copy, and the fourth parameter indicates whether the copy is from host to host, host to device, device to host, or device to device.

err = cudaMemcpy(d_X, h_X, size, cudaMemcpyHostToDevice);

This function returns cudaSuccess if the data was successfully copied. Similar code copies the values in h_Y to d_Y on the device.

Set up parameters for the call to the kernel

Before calling a kernel, the program must determine the number of threads per block and the number blocks in a grid. In the following example, the number of blocks per grid is effectively the number of elements divided by 256. The slightly more complicated calculation guards against grid sizes that aren’t a multiple of the block size.

int threadsPerBlock = 256;
int blocksPerGrid = (numElements + threadsPerBlock - 1) / threadsPerBlock;

Call the kernel

The NVidia Toolkit includes its own compiler that extends C or C++ syntax for calling kernels. The syntax uses a pair of triple angle brackets (<<<  >>>) that follow the name of the kernel. These angle bracket pairs contain two parameters — the number of blocks in the grid, and the number of threads per block. A third parameter is optional.

The parameters of the vectorMult kernel shown in the following example consist of, respectively, the destination vector’s address, the addresses of the two input vectors, and the number of elements of each vector. This kernel call passes control to the GPU. The CUDA system software handles all the details involved in scheduling the individual threads running in the processors of the GPU.

vectorMult <<<blocksPerGrid, threadsPerBlock >>> (d_XY, d_X, d_Y, numElements);

Copy output data back to the host

Copying data from the device back to the host is the reverse of copying data from the host to the device. As before, the first parameter is a pointer to the destination vector, and the second parameter is a pointer to the source vector. The third parameter, cudaMemcpyDeviceToHost, indicates that data will be copied from the device (GPU) to the host. If the memory copy is successful, cudaMemcpy returns cudaSuccess. The code below copies the values in d_XY on the device to the vector h_XY in host memory. Similar code copies the values in d_XX on the device to the vector h_XX in host memory.

err = cudaMemcpy(h_XY, d_XY, size, cudaMemcpyDeviceToHost);

Free device and host memory

The first line below frees the memory allocated for the d_X vector, using the cudaFree function. As is the case with many of the CUDA functions, it returns a value that indicates whether the operation was successful. Any value other than cudaSuccess indicates that an error occurred. To free the host vector, use the C memory deallocation function, free. Similar code deallocates the memory used by the other device and host vectors.

err = cudaFree(d_X);

free(h_X);

Program output

The last four lines show that the computed values for slope and y-intercept agree with those that were used to generate the points on the line, which confirms that the calculations are correct.

[Linear regression of 262144 points]
CUDA kernel launch with 1024 blocks of 256 threads
Sum of x: 34359541760.000000
Sum of y: 34359672832.000000
Sum of xy: 6004765143567284.000000
Sum of x^2: 6004747963793408.000000
Processed 262144 points
Predicted value of m: 1.000000
Computed value of m: 1.0000000000
Predicted value of b: 0.500000
Computed value of b: 0.5000000000

Complete code

For the sake of brevity, I haven’t included the complete source code here in this article. If your curiosity is piqued, you can find the source code for this article, RegressionLine2.cu here: https://github.com/Mark44-AVX/CUDA-vs.-AVX-512.