Self-Study Roadmap: Abstract Algebra, Groups to Galois
Table of Contents
Overview
Roadmap
There are three major areas of mathematics: geometry, analysis, and algebra. This insight gives a roadmap for learning basic abstract algebra for self-study, including the study of groups, rings, fields, and other algebraic structures.
Abstract Algebra Prerequisites
Background expectations
The requirements for self-studying abstract algebra are surprisingly low. You should be familiar with most pre-calculus mathematics and have a basic idea of what proofs are and how they work.
Related resources
For high school mathematics, see my previous insight: Self-Study: Basic High School Mathematics.
For learning proofs, I recommend the following books (in no particular order):
Books for learning proofs
- Velleman — How to Prove It: A Structured Approach
- Bloch — Proofs and Fundamentals: A First Course in Abstract Mathematics
- Hammack — Book of Proof (free online)
Why proofs and set theory matter
These books teach the fundamentals of proof-based mathematics and the basic notation and assumptions of set theory. Both are essential preparation for algebra.
Abstract Algebra for High School Students
Recommended text
If you’re in high school and haven’t taken calculus yet, you can still study a substantial amount of abstract algebra. A good introductory text for this level is Pinter — A Book of Abstract Algebra.
This book covers group theory, basic number theory, ring theory, vector spaces, field theory, and culminates in Galois theory. Chapters are short and the exercises are particularly instructive — not always hard, but very helpful for building understanding.
A First Course in Abstract Algebra (Anderson & Feil)
About this book
Anderson & Feil — A First Course in Abstract Algebra
Book structure and approach
If you’re serious about becoming a mathematician, this is an excellent, pedagogical book. Each chapter contains short exercises within the text, followed by warm-up problems and then more challenging exercises. The selection of problems is strong and well-structured.
Chapter breakdown
First part
First part: A rigorous study of the integers and polynomials to show how these structures are similar; includes discussion of arithmetic modulo n.
Second part
Second part: Detailed ring theory with many examples, with emphasis on unique factorization theorems.
Third part
Third part: Group theory including the standard topics and culminating in the Sylow theorems; groups are presented as geometric objects describing symmetries.
Fourth part
Fourth part: Fields and Galois theory, leading to the proof that some quintic equations are unsolvable by radicals via the fundamental theorem of Galois theory.
Differential Algebra
Liouville’s theorem
Beyond polynomial unsolvability, Liouville’s theorem addresses whether certain integrals can be expressed in elementary terms. This area is part of differential algebra. If you work through Anderson and Feil, you may be interested in a clear introduction to Liouville’s theorem: Rick’s exposition on Liouville’s theorem.
Differential algebra extends further: differential Galois theory studies which differential equations are analytically solvable.
Representation and Character Theory
Quick overview
Representation theory studies how groups and other algebraic objects can be represented as matrices. It has deep links to Fourier analysis and applications in pure group theory, probability, graph theory, and mathematical physics.
Applications and connections
Many modern treatments frame representation theory with modules and algebras, but it’s valuable to see the connection with Fourier analysis. A strong recommendation is Steinberg — Representation Theory of Finite Groups.
Basic Algebraic Geometry
Getting started
Why study algebraic geometry
A solid grasp of abstract algebra benefits from at least an introduction to algebraic geometry, which offers a different perspective on ring theory. For related geometry background, see my geometry recommendations: Self-Study: Pure Geometry. Especially the books by Brannan and Bennett are recommended.
Recommended introduction
A recommended first book in algebraic geometry is Cox, Little, & O’Shea — Ideals, Varieties, and Algorithms. It introduces computational algebraic geometry and commutative algebra via Gröbner bases and elimination theory, covers affine and projective geometry, invariant theory, dimension theory, and includes applications (robotics, automatic theorem proving) as well as standard results like Bézout’s theorem.
Advanced education and experience with mathematics




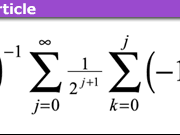


[QUOTE="bacte2013, post: 5530060, member: 495139"]Thank you for the valuable information! How is Steinberg compared to Serre? I need to study the basics of representation theory before diving into the analytic number theory.”I don't know. I know nothing about your goals, your preferences, your background knowledge, etc. The books are clearly very different though. Serre is a graduate text and not an easy one at that. Steinberg is written with undergrads in mind.
Thank you for the valuable information! How is Steinberg compared to Serre? I need to study the basics of representation theory before diving into the analytic number theory.
Great addition to the series!
Great article Micro!