What is the Double Slit? A 5 Minute Introduction

Definition/Summary

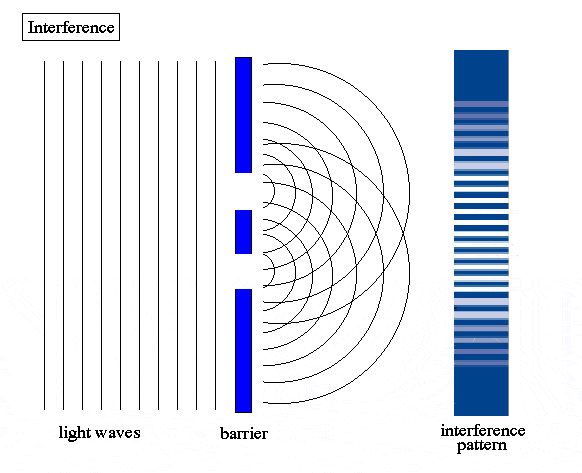
The double-slit is a simple configuration used to demonstrate interference effects in waves.

Equations

At distances that are large compared to the spacing between the slits (i.e. the far-field), the interference maxima (bright fringes) occur at angles such that

$$d \ \sin\theta \ = \ m \ \lambda$$

where

$$\begin{align*}d & = \text{the slit spacing (center-to-center)} \\\theta & = \text{the far-field angle} \\m & = \text{(any integer) the order of the }m^{th} \text{ fringe} \\\lambda & = \text{wavelength}\end{align*}$$

and the minima (dark fringes, or zeroes) occur at

$$d \ \sin\theta \ = \ \left(m+\frac{1}{2}\right) \ \lambda$$

The far-field intensity, as a function of angle, is given by

$$I(\theta) \ = \ 4 I_0 \cdot\cos^2 \delta \cdot\left( \frac{\sin \beta}{\beta} \right)^2$$

where

$$\begin{align*}I_0 & = \text{Central peak intensity due to a single slit of width } b \\\delta & = (k d / 2) \sin \theta= (\pi d / \lambda) \sin \theta \\k & = 2\pi/\lambda \\\beta & = (k b / 2) \sin \theta= (\pi b / \lambda) \sin \theta \\b & = \text{width of each slit}\end{align*}$$

For small angles, one may use the approximation

$$\sin \theta \approx \theta$$

Extended explanation

Explanation

The double-slit is perhaps the simplest configuration that displays interference effects. As there are only 2 paths for the wave, the interference pattern can be easily explained:

If the difference in lengths of the 2 paths is an integer multiple of the wavelength, an interference maximum (or constructive interference) occurs.
If the difference in lengths of the 2 paths is an odd half-integer multiple of the wavelength, an interference minimum, or zero (or destructive interference) occurs. Odd half-integers are ±1/2, ±3/2, etc.
The path difference is simply d sinθ at distances far from the slits, hence its appearance on the left-hand side of the fringe equations.

Remarks on intensity

The expression for I(θ) contains essentially 3 terms:

4 I_0, the central peak intensity
cos^2δ, an interference term due to the path length difference between the 2 wave paths
an “envelope function” equivalent to the diffraction pattern of a single slit of width b

Near field

For distances comparable to the slit spacing, the far-field pattern is not valid. It is, however, straightforward to solve such cases using geometry and trigonometry, and applying the conditions listed above-involving path length difference.

Nonelectromagnetic examples

Aside from optics, the double-slit may arise in physics courses when studying sound waves and quantum mechanics. For sound waves, two speakers are usually used in lieu of the two slits, and the interference effects are often for the near field. In quantum mechanics, the de Broglie wavelength of “matter waves” (eg. electrons) can give rise to interference fringes.

Read the next article on string waves.

Comment Thread