Examples of Prequantum Field Theories IV: Wess-Zumino-Witten-type Theories
Show Complete Series
Part 1: Higher Prequantum Geometry I: The Need for Prequantum Geometry
Part 2: Higher Prequantum Geometry II: The Principle of Extremal Action – Comonadically
Part 3: Higher Prequantum Geometry III: The Global Action Functional — Cohomologically
Part 4: Higher Prequantum Geometry IV: The Covariant Phase Space – Transgressively
Part 5: Higher Prequantum Geometry V: The Local Observables – Lie Theoretically
Part 6: Examples of Prequantum Field Theories I: Gauge Fields
Part 7: Examples of Prequantum Field Theories II: Higher Gauge Fields
Part 8: Examples of Prequantum Field Theories III: Chern-Simons-type Theories
Part 9: Examples of Prequantum Field Theories IV: Wess-Zumino-Witten-type Theories
Part 10: Introduction to Perturbative Quantum Field Theory
At the end of this page, we will have come full circle back to the first article in the series 20 years ago — The M-Theory Conjecture.
We now construct prequantum field theories — in the sense discussed at Higher Prequantum Geometry I, II, III, IV, V — of “WZW-type”, using the methods from Examples of Prequantum Field Theories II, III.
To start with, the traditional Wess-Zumino-Witten (WZW) field theory for a semisimple, simply-connected compact Lie group ##G## is a 2-dimensional sigma-model with target space ##G##, in the sense of the previous Examples of Prequantum Field Theories III, given by a canonical kinetic term, and with topological term that is locally a potential for the left-invariant 3-form ##\langle \theta \wedge [\theta \wedge \theta]\rangle \in \Omega^3(G)_{\mathrm{cl}\atop \mathrm{li}}##, where ##\theta## is the Maurer-Cartan form on ##G##. This means that for ##\{U_i \to G\}## a cover of ##G## by coordinate charts ##U_i \simeq \mathbb{R}^n##, then the classical WZW model is the locally variational classical field theory (in the sense of Higher Prequantum Geometry II) whose local Lagrangian ##L_i## is (in the notation introduced the previous Examples of Prequantum Field Theories III ) ##L_i = (L_{\mathrm{kin}})_i + ((B_i)_\Sigma)_H## for ##B_i \in \Omega^2(U_i)## a 2-form such that ##d B_i = \langle \theta\wedge [\theta\wedge \theta]\rangle|_{U_i}##.
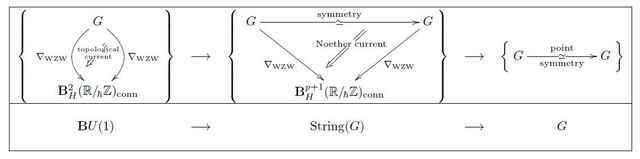
By the previous discussion, in order to prequantize this field theory it is sufficient that we construct a ##U(1)##-gerbe on ##G## whose curvature 3-form is ##\langle \theta \wedge [\theta \wedge\theta]\rangle##. In fact, we may ask for a little more: we ask for the gerbe to be multiplicative in that it carries 2-group structure that covers the group structure on ##G##, hence that it is given by the 2-group extension classified by the smooth universal class ##\mathbf{c} : \mathbf{B}G \longrightarrow \mathbf{B}^3 U(1)##. (This ensures that the WZW model is the corresponding Chern-Simons theory in codimension-2, hence that we have CS/WZW correspondence maybe I’ll talk about that elsewhere).
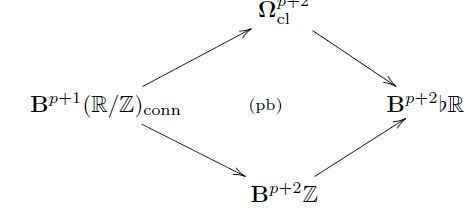
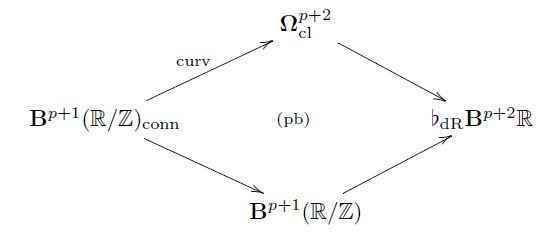
An elegant construction of this prequantization, which will set the scene for the general construction of higher WZW models, proceeds by making use of a universal property of the differential coefficients. Namely one finds that for all ##p \in \mathbb{Z}##, then the moduli stack ##\mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{\mathrm{conn}}## of ##(p+1)##-form connections is the homotopy fiber product of ##\mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})## with ##\mathbf{\Omega}^{p+2}_{\mathrm{cl}}## over ##\flat_{\mathrm{dR}}\mathbf{B}^{p+2}\mathbb{R}## (see at Deligne cohomology — The exact differential cohomology hexagon):
Here “##\flat##” indicates the discrete underlying group, and hence this homotopy pullback says that giving a ##(p+1)##-form connection is equivalent to giving an integral ##(p+2)##-class and a closed ##(p+2)##-form together with a homotopy the identifies the two as cocycles in real cohomology.
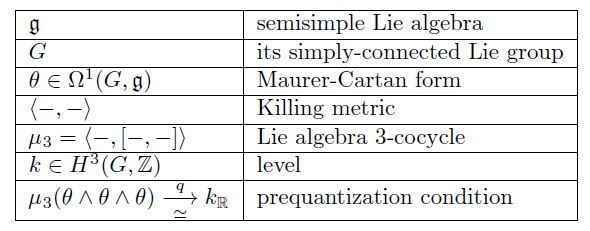
In view of this, consider the following classical Lie theoretic data associated with the semisimple Lie algebra ##\mathfrak{g}##.
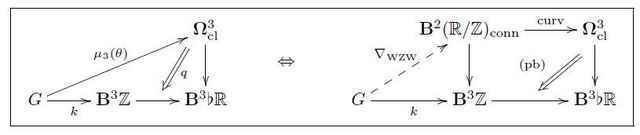
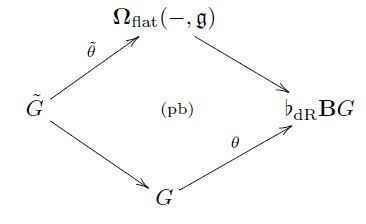
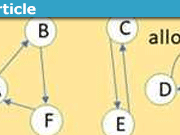
Diagrammatically, this data precisely corresponds to a diagram as shown on the left in the following, and hence the universal property of the homotopy pullback uniquely associates a lift ##\nabla_{\mathrm{WZW}}## as on the right:
This ##\nabla_{\mathrm{WZW}}## is the required prequantum topological term for the 2d WZW model. Hence the prequantum 2d WZW sigma-model field theory is the ##(p = 2)##-dimensional prequantum field theory with target space the group ##G## and with local prequantum Lagrangian, i.e. with Euler-Lagrange gerbe given by
$$
\mathbf{L}
:=
\underset{\mathbf{L}_{\mathrm{kin}}}{\underbrace{ \langle \theta_H \wedge \star \theta_H \rangle}}
+
\underset{\mathbf{L}_{\mathrm{WZW}}}{\underbrace{(\nabla_{\mathrm{WZW}})_H}}
\;\;:\;\;
\Sigma \times G
\longrightarrow
\mathbf{B}^{p+1}_H(\mathbb{R}/_{\!\hbar}\mathbb{Z})_{\mathrm{conn}}
\,.
$$
This prequantization is a de-transgression of a famous traditional construction. To see this, write ##\hat \Omega_k G## for level-##k## Kac-Moody loop group extension of ##G##. This has an adjoint action by the based path group ##P_e G##. Write
$$
\mathrm{String}(G) := P_e G/\!/ \hat \Omega_k G
$$
for the homotopy quotient. This is a differentiable group stack, called the string 2-group [Baez-Crans-Schreiber-Stevenson 07]. It turns out to be the total space of the 2-bundle underlying ##\nabla_{\mathrm{WZW}}##
and it is a de-transgression of the Kac-Moody loop group extension ##\hat L_K G##: transgressing to fields over the circle gives:
The string 2-group also appears again as the 2-group of Noether symmetries, in the sense of Higher Prequantum Geometry V, of the prequantum 2d WZW model. The Noether homotopy fiber sequence for the prequantum 2d WZW model looks as follows [Fiorenza-Rogers-Schreiber 13]:
In fact, this extension is classified by the smooth universal characteristic class ##\mathbf{c} :\mathbf{B}G \longrightarrow \mathbf{B}^3 U(1)##, whose differential refinement gave 3d Chern-Simons theory in Examples of Prequantum Field Theories III.
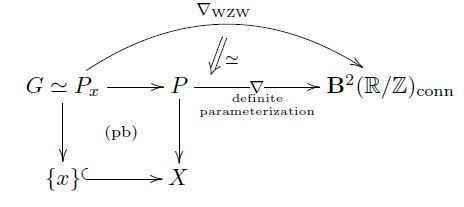
Given a ##G##-principal bundle ##P \to X##, then one may aks for a fiberwise parameterization of ##\nabla_{\mathrm{WZW}}## over ##P##. If such definite parameterization ##\nabla : P \to \mathbf{B}^{2}(\mathbb{R}/\mathbb{Z})_{\mathrm{conn}}## exists, then it defines the prequantum topological term for the parameterized WZW model with target space #P##.
Such a parameterization is equivalent to a lift of a structure group of ##P## through the above extension ##\mathrm{String}(G) \longrightarrow G##. Accordingly, the obstruction to parameterizing ##\nabla_{\mathrm{WZW}}## over ##P## is the universal extension class ##\mathbf{c}## evaluated on ##P##. Specifically for the case that ##G = \mathrm{Spin}\times \mathrm{SU}##, this is the sum of fractional Pontryagin and second Chern class:
$$
\tfrac{1}{2}p_1 – c_2 \in H^4(X,\mathbb{Z})
\,.
$$
The vanishing of this class is the Green-Schwarz anomaly cancellation condition for the 2d field theory describing propagation of the heterotic string on ##X##. This perspective on the Green-Schwarz anomaly via parameterized WZW models had been suggested in [Distler-Sharpe 07]. The prequantum field theory discussed here serves to make this precise and to generalize it to higher dimensional parameterized WZW-type field theories.
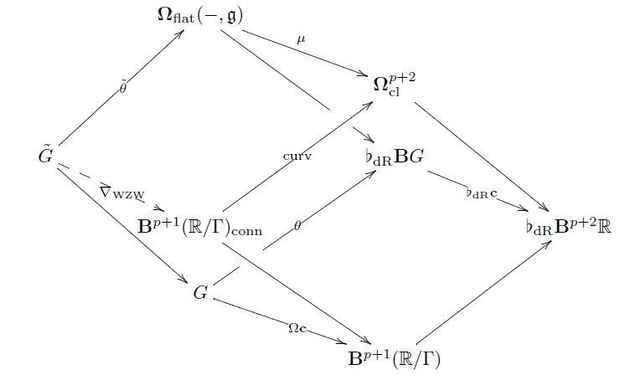
Generally, given any ##L_\infty##-cocycle ##\mu : \mathbf{B}\mathfrak{g} \longrightarrow \mathbf{B}^{p+2}\mathbb{R}## as in Examples of Prequantum Field Theories II with induced smooth ##\infty##-group cocycle ##\mathbf{c} : \mathbf{B}G \longrightarrow \mathbf{B}^{p+2}(\mathbb{R}/\Gamma)## as in Examples of Prequantum Field Theories III, then there is a higher analog of the universal construction of the WZW-type topological term ##\nabla_{\mathrm{WZW}}##.
First of all, the homotopy pullback characterization of ##\mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{\mathrm{conn}}## refines to one that does not just involve the geometrically discrete coefficients ##\mathbf{B}^{p+2}\mathbb{Z}##, but the smooth coefficients ##\mathbf{B}^{p+1}(\mathbb{R}/\mathbb{R})##
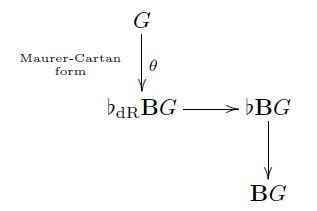
Here ##\flat_{\mathrm{dR}}(-)## denotes the homotopy fiber of the canonical map ##\flat(-)\longrightarrow (-)## embedding the underlying discrete smooth structure of any object into the given smooth object. A key aspect of the theory is that the further homotopy fiber of ##\flat_{\mathrm{dR}}(-) \longrightarrow \flat(-)## has the interpretation of being the Maurer-Cartan form ##\theta## on the given
smooth ##\infty##-groupoid.
Or rather, one finds that ##\flat_{\mathrm{dR}}\mathbf{B}G \simeq \mathbf{\Omega}_{\mathrm{flat}}^{1 \leq \bullet\leq p+2}(-,\mathfrak{g})## is the coefficient for “hypercohomology” in flat ##\mathfrak{g}##-valued differential forms, hence for ##G## a higher smooth group then its Maurer-Cartan form ##\theta## is not, in general, a globally defined differential form, but instead a system of locally defined forms with higher coherent gluing data.
But one may universally force ##\theta## to become globally defined, so to speak, by pulling it back along the inclusion ##\mathbf{\Omega}_{\mathrm{flat}}(-,\mathfrak{g})## of the globally defined flat ##\mathfrak{g}##-valued forms. This defines a differential extension ##\tilde G## of ##G## equipped with a globally defined Maurer-Cartan form ##\tilde \theta##, by the following homotopy pullback diagram
When ##G## is an ordinary Lie group, then it so happens that ##\flat_{\mathrm{dr}}\mathbf{B}G \simeq \mathbf{\Omega}_{\mathrm{flat}}(-,\mathfrak{g})##, and so in this case ##\tilde G \simeq G## and ##\tilde \theta \simeq \theta##, so that nothing new happens.
At the other extreme, when ##G = \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})##, then ##\theta \simeq \mathrm{curv}## as above, and so in this case one find that ##\tilde G## is ##\mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{\mathrm{conn}}## and that ##\tilde \theta \simeq F_{(-)}## is the map that sends an ##(p+1)##-form connection to its globally defined curvature ##(p+2)##-form.
More generally these two extreme cases mix: when ##G## is a ##\mathbf{B}^p (\mathbb{R}/Z)##-extension of an ordinary Lie group,
then ##\tilde G## is a twisted product of ##G## with ##\mathbf{B}^{p}(\mathbb{R}/\mathbb{Z})_{\mathrm{conn}}##, hence then
a single map
$$
(\phi,B) : \Sigma \longrightarrow \tilde G
$$
is a pair consisting of an ordinary sigma-model field ##\phi## together with a ##\phi##-twisted ##p##-form connection on ##\Sigma##.
Hence the construction of ##\tilde G## is a twisted generalization of the construction of differential coefficients. In particular, given an ##L_\infty##-cocycle ##\mu : \mathbf{B}\mathfrak{g}\longrightarrow \mathbf{B}^{p+2}\mathbb{R}## Lie-integrating to an ##\infty##-group cocycle ##\mathbf{c} : \mathbf{B}G \to \mathbf{B}^{p+2}(\mathbb{R}/\Gamma)##, then it Lie integrates to a
prequantum topological term ##\nabla_{\mathrm{WZW}} : \tilde G \longrightarrow \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{\mathrm{conn}}## via the universal dashed map in the following induced diagram:
This construction provides a large supply of prequantum Wess-Zumino-Witten type field theories. Indeed, by the discussion in Examples of Prequantum Field Theories II, from every ##L_\infty##-algebroid there emanates a bouquet of ##L_\infty##-extensions with ##L_\infty##-cocycles on them, hence for every WZW-type sigma model prequantum field theories we find a whole bouquet of prequantum field theories emanating from it.
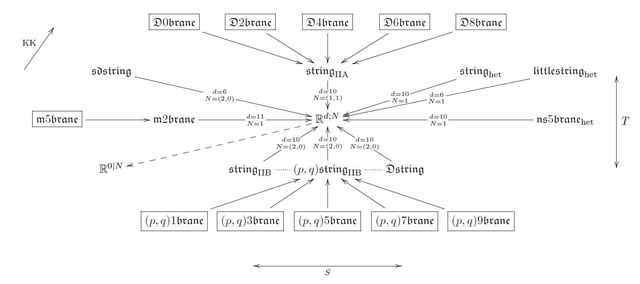
Therefore it is interesting to consider the simplest non-trivial ##L_\infty##-algebroids and see which bouquets of prequantum field theories they induce. The abelian line Lie algebra ##\mathbb{R}## is arguably the simplest non-vanishing ##L_\infty##-algebroid, but it is in fact a little too simple for this purpose, the bouquet it induces is not interesting. But all of the above generalizes essentially verbatim to super-algebra and super-geometry. In super-Lie-algebra theory, we have the “odd lines” ##\mathbb{R}^{0|q}##, i.e.the superpoints. The bouquet which emanates from these turns out to be remarkably rich [Fiorenza-Sati-Schreiber 13], it gives the entire ##p##-brane spectrum of string theory/M-theory, as already discussed in the previous article in the series Emergence from the Superpoint.
Each entry in this diagram denotes a super ##L_\infty##-algebra extension of some super Minkowski spacetime ##\mathbb{R}^{d-1,1|N}## (regarded as the corresponding supersymmetry super Lie algebra), and each arrow denotes a super-##L_\infty##-extension classified by a ##p+2## cocycle for some ##p##. By the above general construction, this cocycle induces a ##(p+1)##-dimensional WZW-type sigma-model prequantum field theory with target space a higher extension of super-Minkowski spacetime, and the names of the super ##L_\infty##-algebras in the above diagram correspond to the traditional names of these super ##p##-branes.
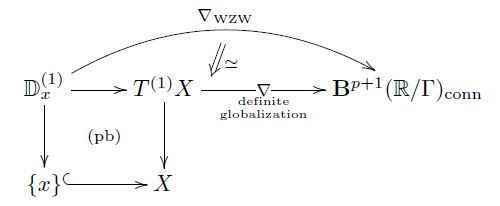
As for the traditional WZW-models, all of this structure naturally generalizes to its parameterized versions: given any higher extended super Minkowski spacetime ##V## equipped with a prequantum topological term ##\nabla_{\mathrm{WZW}} : V \longrightarrow \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{\mathrm{conn}}## for a super ##p##-brane sigma model, we may ask for globalizations of ##\nabla## over ##V##-manifolds (##V##-etale stacks) ##X##, hence for topological term ##\nabla## on all of ##X## that is suitably equivalent on each infinitesimal disk ##\mathbb{D}^X_x \simeq \mathbb{D}^V_e## to ##\nabla_{\mathrm{WZW}}##.
Such globalizations serve as prequantum topological terms for WZW-type sigma-models describing the propagation of super ##p##-branes
on ##V##-manifolds ##X## ([Bergshoeff-Sezgin-Townsend 86/87]). One finds (see the lecture notes Structure Theory for Higher WZW Terms) that such globalizations equip the higher frame bundle of ##X## with a lift of its structure group through a canonical map ##\mathbf{Stab}_{\mathrm{GL}(V)}(\nabla) \longrightarrow \mathrm{GL}(V)## from the homotopy stabilizer group of the WZW term,
in direct analogy to the previous examples. Apart from “canceling the classical anomalies”” of making the super ##p##-brane WZW-type sigma-model be globally defined on ##X##, such a lift induces metric structure on ##X##:
Since the homotopy stabilization of ##\nabla##, in particular, stabilizes its curvature form, there is a reduction of the structure group of the ##V##-manifold in direct analogy to how a globalization of the “associative” 3-form ##\alpha## on ##\mathbb{R}^7## equips a 7-manifold with ##G_2##-structure (see here). For the above super ##p##-brane models the relevant stabilizer is the spin-cover of
the Lorentz group (due to a neat argument by John Huerta, see at Super Cartan Geometry — Definite superforms), and hence globalizing the prequantum ##p##-brane model over ##X##, in particular, induces orthogonal structure on ##X##, hence equips ##X## with a field configuration of supergravity.
Given such a globalization of a topological term ##\nabla## over a ##V##-manifold ##X##, it is natural to require it to be infinitesimally integrable. In the present example, this comes out to imply that the torsion of the orthogonal structure on ##X## vanishes. This is particularly interesting at the top end of the brane bouquet: for globalization over an 11-dimensional supermanifold, the vanishing of the torsion is equivalent to ##X## satisfying the equations of motion of 11-dimensional gravity [Candiello-Lechner 93]. The Noether charges of the corresponding WZW-type prequantum field theory are the supergravity BPS-charges [Sati-Schreiber 15].
Here the relation to ##G_2##-structure is more than an analogy. We may naturally lift the topological term for the M2-brane sigma-model from ##\mathbb{R}/\mathbb{Z}##-coefficients to ##\mathbb{C}/\mathbb{Z}##-coefficients by adding ##\alpha : \mathbb{R}^{10,1\vert \mathbf{32}} \to \mathbb{R}^7 \to \mathbf{\Omega}^3_{\mathrm{cl}}##. Then a globalization of the complex linear combination
$$
\nabla_{\mathrm{M2}} + i \alpha : \mathbb{R}^{10,1\vert \mathbf{32}} \longrightarrow \mathbf{B}^{3}(\mathbb{C}/\Gamma)_{\mathrm{conn}}
$$
over an 11-dimensional supermanifold ##X## equips ##X## with the structure of a ##G_2##-fibration over a 4-dimensional ##N=1## supergravity spacetime. The volume holonomy of ##\nabla_{\mathrm{M2}} + i \alpha## around supersymmetric 3-cycles are the “M2-instanton contributions”. This setup of 11-dimensional supergravity Kaluza-Klein-compactified on ##G_2##-manifolds to 4 spacetime dimensions and with the prequantum M2/M5-brane charges and instantons included — known as M-theory on G2-manifolds — comes at least close to capturing the qualitative structure of experimentally observed fundamental physics.
This shows that there is some interesting physics encoded in those prequantum field theories that are canonically induced from a minimum of input data.
I am a researcher in the department Algebra, Geometry and Mathematical Physics of the Institute of Mathematics at the Czech Academy of the Sciences (CAS) in Prague.
Presently I am on leave at the Max Planck Institute for Mathematics in Bonn.



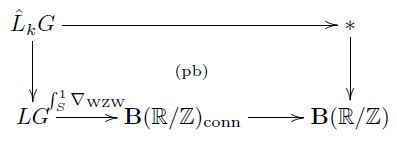






[QUOTE=”glaucousNoise, post: 5293268, member: 570615″]what’s the point of this mystical, arcane stuff? It seems like you’ve used extremely dense, convoluted language to construct a model that doesn’t appear to describe nature.[/QUOTE]
He is a mathematical physicist. Its the type of thing they do – eg delve deeply into the underlying mathematical structure of our theories.
My background is math, and the detail of what he writes is way beyond my present level. But you can still read it and glean bits and pieces here and there that are interesting.
Thanks
Bill
[QUOTE=”David Corfield, post: 5276291, member: 573332″]”The bouquet which emanates form these…” should be FROM. Also various pieces of latex didn’t compile[/QUOTE]
Thanks for catching this! All fixed now.
[QUOTE=”David Corfield, post: 5276291, member: 573332″]Have you seen any other interesting bouquets?[/QUOTE]
We had looked a bit into the higher tower of cocycles emanating from a semisimple Lie algebra, which in the first stage yields 3d-Chern-Simons theory on G-gauge fields, in the second stage yields [URL=’http://ncatlab.org/schreiber/show/7d+Chern-Simons+theory+and+the+5-brane’]7d-Chern-Simons theory[/URL] on String(G)-higher gauge fields, and then in the next stage yields an 11-dimensional CS theory that Hisham [URL=’http://ncatlab.org/nlab/show/M9-brane#Sati14′]argues[/URL] is related to the “M9-brane”.
[QUOTE=”David Corfield, post: 5276291, member: 573332″]I see there is some gauge theoretic interest in complex analytic superspaces, such as p. 12 of [URL]http://arxiv.org/abs/1507.03048[/URL].[/QUOTE]
Yes, superstring perturbation theory in principle is all about complex analytic supergeometry, due to it being all about [URL=’http://ncatlab.org/nlab/show/super+Riemann+surface’]super Riemann surfaces[/URL].
what's the point of this mystical, arcane stuff? It seems like you've used extremely dense, convoluted language to construct a model that doesn't appear to describe nature.I'm just a humble biologist here.
"The bouquet which emanates form these…" should be FROM. Also various pieces of latex didn't compile.Have you seen any other interesting bouquets? What would happen in the complex analytic world? I see there is some gauge theoretic interest in complex analytic superspaces, $mathbb{C]^{p|q)$, such as p. 12 of http://arxiv.org/abs/1507.03048.