Moment of Inertia: Definitions, Formulas & Tensor Guide

Definition / Summary

The moment of inertia is a property of a rigid body that relates torque (rotational force) to rotational acceleration in the same way mass relates linear force to linear acceleration. It has units of mass times distance squared (M·L²) and is always defined with respect to a specific axis: the same rigid body generally has different moments of inertia for different axes. The moment of inertia of a composite body equals the sum of the moments of inertia of its parts relative to the same axis.

Key equations

Moment of inertia (continuous body) about an axis, where r is the perpendicular distance from that axis and ρ is density:

I = ∫ r² dm = ∫ ρ(x,y,z) r² dV

Angular momentum about the centre of mass (C):

L_C = I_C · ω (principal-axis case)

L_C = Ĩ_C · ω (general tensor case, where Ĩ_C is the inertia tensor)

About a general point P:

L_P = I_C · ω + (PC) × m v_C (principal-axis case)

L_P = Ĩ_C · ω + (PC) × m v_C (general tensor case)

Kinetic energy (translation + rotation):

KE = ½ m v_C² + KE_rot = KE_trans + KE_rot

KE_rot = ½ ω · L_C = ½ I_C ω² (principal-axis)

KE_rot = ½ ω · L_C = ½ ωᵀ Ĩ_C ω (general tensor)

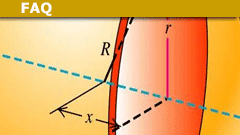
Parallel-axis theorem (distance d between parallel axes):

I = I_C + m d²

Tensor (vector displacement d between reference points):

Ĩ = Ĩ_C − m ( d × ( d × · ) )

Small-angle period of a physical pendulum:

T = 2π sqrt( I / (m g h) ) (h = distance from pivot to center of mass)

Radius of gyration (about an axis):

k = sqrt( I / m ) (distance at which an ideal point-mass would produce the same I)

Extended explanation

About “a point” vs “an axis”

Strictly speaking, moment of inertia is defined about an axis, not about a point. In two-dimensional problems authors commonly write “about a point” to mean “about the axis perpendicular to the plane at that point.” That shorthand is acceptable in 2D but not in full 3D. By contrast, angular momentum may be described relative to a point, and the inertia tensor is defined about a point (it yields moments of inertia about any axis through that point).

Axis of rotation

If one point of a rigid body is fixed, the instantaneous axis of rotation is the line of stationary points in the body. For a freely moving rigid body the axis of rotation is often taken through the center of mass; any parallel axis can be used with appropriate application of the parallel-axis theorem.

Derivation idea (kinetic energy)

For a rigid body without rotation, every part has the same speed and KE = ½ m v_C². If the body rotates, the speed of each element depends on its distance from the instantaneous axis. Divide the body into infinitesimal mass elements δm_i at perpendicular distances r_i from the axis. Each element’s kinetic energy is

KE_i = ½ δm_i v_i² = ½ δm_i (ω r_i)²

Summing and taking the continuous limit gives

KE = ½ ω² ∑ δm_i r_i² = ½ I ω², where I = ∑ δm_i r_i² → I = ∫ r² dm

Common formulas (useful cases)

Four principal formulas often used (consistent variable definitions):

• Point mass: I = m r² (r = perpendicular distance to axis)
• Uniform rod, mass m, length 2L, axis through midpoint perpendicular to length: I = (1/3) m L²
• Rectangular lamina, mass m, length 2L (axis bisecting length): I = (1/3) m L²
• Circular disc, mass m, radius R, axis through center perpendicular to disc: I = ½ m R²

For extended tables of standard moments of inertia see reference lists (Wikipedia or mechanics texts).

Moment of inertia tensor

Angular momentum is not necessarily parallel to angular velocity unless rotation occurs about a principal axis. The inertia tensor Ĩ converts angular velocity into angular momentum:

L = Ĩ · ω

The eigenvectors of Ĩ are the principal axes and their eigenvalues are the corresponding principal moments I₁, I₂, I₃. Special cases include:

• Three distinct perpendicular principal axes (most rigid bodies).
• A plane of equal eigenvalues and a perpendicular axis (bodies with one symmetry axis).
• Isotropic case: identical moments in all directions (spherical symmetry).

Angular momentum and torque

The net torque about a chosen point equals the time rate of change of angular momentum about that point:

τ_net = dL/dt = d/dt ( Ĩ · ω ) = Ĩ · dω/dt + (dĨ/dt) · ω

This relation requires that the chosen point is stationary or moves parallel to the center-of-mass velocity (for example, the center of mass itself or the instantaneous contact point when rolling). Because the inertia tensor is fixed in the body but not fixed in space, dĨ/dt is generally nonzero unless ω lies along a principal axis.

If ω is along a principal axis with eigenvalue I_A, then

L = I_A ω and τ_net = I_A · dω/dt for that axis.

Rotating (body-fixed) frame — Euler’s equations

In a frame fixed in the body (Ĩ is constant) an extra Coriolis-type term appears:

τ_net = dL/dt + ω × L = Ĩ · dω/dt + ω × (Ĩ · ω)

In components along body-fixed principal axes with moments I₁, I₂, I₃, Euler’s equations are:

τ₁ = I₁ dω₁/dt + (I₃ − I₂) ω₂ ω₃

τ₂ = I₂ dω₂/dt + (I₁ − I₃) ω₃ ω₁

τ₃ = I₃ dω₃/dt + (I₂ − I₁) ω₁ ω₂

Composite bodies and the parallel-axis theorem

When assembling a composite body, use moments (and tensors) computed about the composite center of mass. For each part, convert its moment about its own center of mass to the composite center using the parallel-axis theorem:

I = I_C + m d² where d is the perpendicular distance between the two parallel axes.

Perpendicular-axis theorem (lamina)

For a planar lamina (thin, two-dimensional body) with axes x and y in the plane and z perpendicular to it:

I_z = I_x + I_y

Terminology and common confusions

“Moment of inertia” is sometimes called “mass moment of inertia” to distinguish it from the second moment of area (also called “moment of inertia” in structural engineering). The second moment of area has units L⁴ and measures bending resistance; mass moment of inertia has units M·L² and relates torque to angular acceleration (τ = I α).

Further reading and discussion:

Comment thread on PhysicsForums