Operators Definition and 1000 Threads
-

Undergrad Quarks and isospin ladder operators
Hi, guys. This is actually a question about quantum mechanics, but since the context in which it appeared is particle physics, I'll post it here. On Thompson's book (page 227, equation (9.32)), we have $$T_+ |d\bar{u}\rangle = |u\bar{u}\rangle - |d\bar{d}\rangle$$ But I thought...- Xico Sim
- Thread
- Isospin Ladder operators Operators Quarks
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-

Undergrad Sum of squares of 2 non-commutating operators
Prof Adams does something rather strange, starting from 14:35 minutes in this lecture -- http://ocw.mit.edu/courses/physics/8-04-quantum-physics-i-spring-2013/lecture-videos/lecture-9/ He reminds us that for complex scalars, ##c^2+d^2=(c-id)(c+id)## and then proceeds to do the same with...- Swamp Thing
- Thread
- Operators Squares Sum
- Replies: 4
- Forum: Quantum Physics
-
&
Graduate Time dependence of field operators
In field theory we most of deal with theories whose Lagrangian densities are of the form (sticking to scalar fields for simplicity) $$\mathcal{L}= -\frac{1}{2}\partial_{\mu}\phi\partial^{\mu}\phi - \frac{1}{2}m_{\phi}^{2}\phi^{2} + \cdots$$ where ##\partial := \frac{\partial}{\partial x^{\mu}}##...- "Don't panic!"
- Thread
- Field Field operators Momentum Operators Qft Scalar field Time Time dependence Time dependent
- Replies: 12
- Forum: Quantum Physics
-

How Does Time Evolution Affect Quantum Operator Matrix Elements?
Homework Statement [/B] For a general operator ## \hat{O}##, let ##\hat{O}_{mn}(t)## be defined as: $$ \hat{O_{mn}}(t) = \int u^{*}_{m}(x,t) \hat{O} u_{n}(x,t) $$ and $$ \hat{O_{mn}} = \int u^{*}_{m}(x) \hat{O} u_{n}(x) $$ ##u_{m}## and ##u_{n}## are energy eigenstates with corresponding...- bananabandana
- Thread
- Commutator Evolution Expectation Operator Operators Time Time evolution
- Replies: 7
- Forum: Advanced Physics Homework Help
-

Undergrad Why does a sum of operators act on the state like this?
I'm reading through my quantum physics lecture notes (see page 216 of the lecture notes for more details) and under the ladder operators section there is a discussion of the expectation value of ##L_x## for a state ##\psi = R(r) \left( \sqrt{ \frac{2}{3}} Y_{11} - \sqrt{ \frac{1}{3}} Y_{10}...- Harry Smith
- Thread
- Act Operators Quantum State Sum
- Replies: 6
- Forum: Quantum Physics
-

Undergrad Second quantization and creation/annih. operators
I'd like some help with something in this introduction to second quantization ... http://yclept.ucdavis.edu/course/242/Class.html They start by considering two operators ##a## and ##a^\dagger## such that ##[a,a^\dagger]=1## and they are adjoint to each other. Also introduced is a state...- Swamp Thing
- Thread
- Operators Quantization Second quantization
- Replies: 3
- Forum: Quantum Physics
-
C
Graduate Time-ordering fermion operators
If A and B are fermionic operators, and T the time-ordering operator, then the standard definition is T(AB) = AB, if B precedes A = - BA, if A precedes B. Why is there a negative sign? If A and B are space-like separated then it makes sense to assume that A and B anticommute. But...- Coriolis1
- Thread
- Fermion Fermions Operators Quantum field theory
- Replies: 1
- Forum: Quantum Physics
-
D
Undergrad Exponential Operators: Inverting, Rearranging, Expanding
If I rearrange an equation invoving exponentials of operators and I take ex to the opposite side of the equation it becomes e-x. What happens if I try to take eA to the opposite side ? I know a exponential of operators can be expanded as a Taylor series which involves products of matrices but...- dyn
- Thread
- Exponential Operators
- Replies: 3
- Forum: Linear and Abstract Algebra
-

MHB Different Kinds of Quantum Computing Measurement Operators
So in quantum mechanics, there are at least three different kinds of measurement operators: the General, the Projective, and the Positive Operator-Valued (POVM). They have different properties and relationships. In a typical QM book, these are not delineated, but in Quantum Computing they are...- Ackbach
- Thread
- Computing Measurement Operators Quantum Quantum computing
- Replies: 2
- Forum: Quantum Physics
-
F
Undergrad Inner products and adjoint operators
I'm trying to prove the following relation $$\langle\psi\lvert \hat{A}^{\dagger}\rvert\phi\rangle =\langle\phi\lvert \hat{A}\rvert\psi\rangle^{\ast}$$ where ##\lvert\phi\rangle## and ##\lvert\phi\rangle## are state vectors and ##\hat{A}^{\dagger}## is the adjoint of some operator ##\hat{A}##...- Frank Castle
- Thread
- Inner product Operators Operators on hilbert space Quantum mechanics
- Replies: 8
- Forum: Quantum Physics
-

Commutator relations of field operators
Here is the question: By using the equality (for boson) ---------------------------------------- (1) Prove that Background: Currently I'm learning things about second quantization in the book "Advanced Quantum Mechanics"(Franz Schwabl). Given the creation and annihilation operators(), define...- QuantumRose
- Thread
- Commutator Field Field operators Operators Relations
- Replies: 2
- Forum: Advanced Physics Homework Help
-
P
Representing spin operators in alternate basis
Homework Statement I want to find the matrix representation of the ##\hat{S}_x,\hat{S}_y,\hat{S}_z## and ##\hat{S}^2## operators in the ##S_x## basis (is it more correct to say the ##x## basis, ##S_x## basis or the ##\hat{S}_x## basis?). Homework Equations...- pondzo
- Thread
- Basis Operators Quantum mechanics Spin
- Replies: 3
- Forum: Advanced Physics Homework Help
-
C
Undergrad Raising and lowering operators for a composite isospin SU(2)
Consider pion states composed of ##q \bar q## pairs where ##q \in \left\{u,d \right\}## transforms under an ##SU(2)## isospin flavour symmetry. These bound states transform in the tensor product ##R_1 \otimes R_2## of two representations ##(R_1, R_2)## of ##SU(2)##. Take ##R_2## as the...- CAF123
- Thread
- Composite Isospin Operators Su(2)
- Replies: 9
- Forum: High Energy, Nuclear, Particle Physics
-

Commuting Operators: Understanding How M1,M2 & M3 Work Together
Homework Statement It is known that ##M_1,M_2, M_3## commute with each other but I don't see how the second line is achieved even though it says that it's using that ##M_1## and ##M_2## commute?- Raptor112
- Thread
- eigenstates operators
- Replies: 5
- Forum: Introductory Physics Homework Help
-
L
Similarity Transformation Involving Operators
Homework Statement Virtually all quantum mechanical calculations involving the harmonic oscillator can be done in terms of the creation and destruction operators and by satisfying the commutation relation \left[a,a^{\dagger}\right] = 1 (A) Compute the similarity transformation...- loginorsinup
- Thread
- Linear algebra Matrices Operators Quantum mechanics Transformation
- Replies: 22
- Forum: Advanced Physics Homework Help
-

Undergrad When can one clear the operator
Hi all! I'm having problems understanding the operator algebra. Particularly in this case: Suppose I have this projection ## \langle \Phi_{1} | \hat{A} | \Phi_{2} \rangle ## where the ##\phi's ## have an orthonormal countable basis. If I do a state expansion on both sides then I suppose I'd get...- Ernesto Paas
- Thread
- Operator Operators Projection
- Replies: 8
- Forum: Quantum Physics
-

Undergrad If operators commute then eigenstates are shared
I'm confused about the statement that if operators commute then eigenstates are shared. My main confusion is this one: ##L^2## commutes with ##L_i##. Then these two share eigenstates. But ##L_x## and ##L_y## do not commute, so they don't share eigenstates. Isn't this violating some type of...- davidbenari
- Thread
- Commute Eigenstates Operators
- Replies: 14
- Forum: Quantum Physics
-
C
Quantum operators and commutation relations
Homework Statement Given the mode expansion of the quantum field ##\phi## and the conjugate field one can derive $$\mathbf P = \int \frac{d^3 \mathbf p}{(2\pi)^3 2 \omega(\mathbf p)} \mathbf p a(\mathbf p)^{\dagger} a(\mathbf p)$$ By writing $$e^X = \text{lim}_{n \rightarrow \infty}...- CAF123
- Thread
- Commutation Operators Quantum Relations
- Replies: 8
- Forum: Advanced Physics Homework Help
-
T
Undergrad Non-commuting operators on the same eigenfunctions
In Griffiths chapter 4 (pg. 179-180) there is an example (Ex. 4.3) that details the expectation value of ## S_x ##, ##S_y##, and ##S_z## of a spin 1/2 particle in a magnetic field. In this example, they find an eigenvector of ## H## (which commutes with ## S_z##) but then use this same...- TheCanadian
- Thread
- Eigenfunctions Operators
- Replies: 1
- Forum: Quantum Physics
-
G
Diagonalizing a polynomial of operators (Quantum Mechanics)
The problem asks for the diagonalization of (a(p^2)+b(x^2))^n, where x and p are position and momentum operators with the commutation relation [x,p]=ihbar. a and b are real on-zero numbers and n is a positive non-zero integer.I know that it is not a good way to use the matrix diagonalization...- Ghazaleh_Zm
- Thread
- Diagonalization Mechanics Operators Polynomial Quantum Quantum mechanics
- Replies: 7
- Forum: Advanced Physics Homework Help
-

Undergrad Aren't all linear operators one-to-one and onto?
Let W be a vector space and let A be a linear operator W --> W. Isn't it the case that for any such A, the kernel of A is the zero vector and the range is all of W? And that it is one-to-one from linearity? I ask because an author I am reading goes through a lot of steps to show that a certain...- pellman
- Thread
- Linear linear operators Operators
- Replies: 10
- Forum: Linear and Abstract Algebra
-

Undergrad Expression for Uncertainty of Arbitrary Operator
Hello all, as far as I can see this question is not posted already, my apologies if it is and please provide a link. But I'm watching this video on youtube: And at 22:38 there's an expression given for the uncertainty of an arbitrary operator Q, however I'm concerned the expression is incorrect...- DrPapper
- Thread
- Expression Operator Operators Quantum mechanics Uncertainty
- Replies: 3
- Forum: Quantum Physics
-
Z
Undergrad How exactly does squaring operators (e.g. <p^2> work?
I'm having to essentially piece together a framework of background knowledge to understand parts of a QM class in which I'm lacking prerequisites; one of the things that I noticed that really confused me was the square of the momentum operator <p>, and how that translated into the integrand of...- Zacarias Nason
- Thread
- Operators Work
- Replies: 5
- Forum: Quantum Physics
-
L
Graduate Eigenstates of Orbital Angular Momentum
Recently I've been studying Angular Momentum in Quantum Mechanics and I have a doubt about the eigenstates of orbital angular momentum in the position representation and the relation to the spherical harmonics. First of all, we consider the angular momentum operators L^2 and L_z. We know that...- leo.
- Thread
- Angular Angular momentum Eigenfunctions Eigenstates Hilbert space Momentum Operators Orbital Orbital angular momentum Spherical harmonics
- Replies: 7
- Forum: Quantum Physics
-

Finding expectation values for given operators
Homework Statement The Hamiltonian of an electron in solids is given by H. We know that H is an Hermitian operator, it satisfies the following eigenvalue equation: H|Φn> = εn|Φn> Let us define the following operators in terms of H as: U = e^[(iHt)/ħ] , S = sin[(Ht)/ħ] , G = (ε -...- phys-student
- Thread
- Expectation Expectation value Expectation values Operators Quantum
- Replies: 5
- Forum: Introductory Physics Homework Help
-
J
Graduate Raising and Lowering Operators
In Griffith and Shankar, the raising and lowering operator seem to appear from nowhere, but it seems really elegant. Where do they come from, is it some corollary from certain mathematical structure? Can anyone give a brief explanation?- jjohnson
- Thread
- Operators
- Replies: 2
- Forum: Quantum Physics
-
B
Graduate Do ladder operators give integer multiples of ћ?
Say I apply a raising operator to the spin state |2,-1>, then by using the the equation S+|s,ms> = ћ*sqrt(s(s+1) - ms(ms+1))|s,ms+1> I get, S+|2,-1> = sqrt(6)ћ|2,0> Does this correspond to a physical eigenvalue or should I disregard it and only take states with integer multiples of ћ as...- baouba
- Thread
- Integer Ladder operators Operators
- Replies: 5
- Forum: Quantum Physics
-

Graduate Hermitian Operators: Understanding How They Work
We know that operators can be represented by matrices. Every operator in finite-dimensional space can be represented by a matrix in a given basis in this space. If the transpose conjugate of the matrix representation of an operator in a given basis is the same of the original matrix...- amjad-sh
- Thread
- Hermitian Operators
- Replies: 16
- Forum: Quantum Physics
-

Matrix Representation for Combined Ladder Operators
Due to the definition of spin-up (in my project ), \begin{eqnarray} \sigma_+ = \begin{bmatrix} 0 & 2 \\ 0 & 0 \\ \end{bmatrix} \end{eqnarray} as opposed to \begin{eqnarray} \sigma_+ = \begin{bmatrix} 0 & 1 \\ 0 & 0 \\ \end{bmatrix} \end{eqnarray} and the annihilation operator is...- Raptor112
- Thread
- Ladder operator Ladder operators Matrices Matrix Operators Representation
- Replies: 18
- Forum: Advanced Physics Homework Help
-

Spin Angular Momentum and Operators
Homework Statement Attached Homework Equations ##J_+|j,m⟩ = ћ\sqrt{j(j+1)-m(m+1)} |j,m+1⟩## ##J_-|j,m⟩ = ћ\sqrt{j(j+1)-m(m-1)} |j,m-1⟩## ##J_z|j,m⟩ = mћ |j,m⟩## ##J^2|j,m⟩ = ћ^2j(j+1) |j,m⟩## The Attempt at a Solution Hi there, For part a, the expression we're looking for is given, but...- samjohnny
- Thread
- Angular Angular momentum Momentum Operators Spin
- Replies: 14
- Forum: Advanced Physics Homework Help
-
M
Harmonic Oscillator and Ladder Operators
Homework Statement Consider a linear harmonic oscillator with the solution defined by the ladder operators a and a†. Use the number basis |n⟩ to do the following. a) Construct a linear combination of |0⟩ and |1⟩ to form a state |ψ⟩ such that ⟨ψ|X|ψ⟩ is as large as possible. b) Suppose that...- MFAHH
- Thread
- Harmonic Harmonic oscillator Ladder operators Operators Oscillator
- Replies: 21
- Forum: Advanced Physics Homework Help
-
H
Graduate Matrix representation of operators
Let the operators ##\hat{A}## and ##\hat{B}## be ##-i\hbar\frac{\partial}{\partial x}## and ##x## respectively. Representing these linear operators by matrices, and a wave function ##\Psi(x)## by a column vector u, by the associativity of matrix multiplication, we have...- Happiness
- Thread
- Matrix Operators Representation
- Replies: 1
- Forum: Quantum Physics
-
H
Graduate Why is (5.302) an Approximation of Exponential Operators?
Why is (5.302) an approximation instead of an equality? Let ##T## be the operator ##\frac{p_x^2}{2m}##. By the law of indices, we should have ##e^{-\frac{i}{\hbar}(T+V)\Delta t}=e^{-\frac{i}{\hbar}T\Delta t} e^{-\frac{i}{\hbar}V\Delta t}## exactly. Is it because ##T## and ##V## do not commute...- Happiness
- Thread
- Exponential Operators
- Replies: 17
- Forum: Quantum Physics
-

MHB Quantum Computing: Positive Operators are Hermitian
Exercise 2.24 on page 71 of Nielsen and Chuang's Quantum Computation and Quantum Information asks the reader to show that a positive operator is necessarily Hermitian. There is a hint given; namely, that you first show an arbitrary operator can be written $A=B+iC$, where $B$ and $C$ are...- Ackbach
- Thread
- Computing Hermitian Operators Positive Quantum Quantum computing
- Replies: 2
- Forum: Quantum Physics
-
Q
Undergrad Ceiling and floor operators used for min max
I remember seeing somewhere people using symbols for ceiling and floor operators together with super/subscripts as substitutes for min and max. Example: \lceil x \rceil ^k to mean min(x,k). Has anyone ever seen this? Where? Thanks!- quantum__2000
- Thread
- Max Operators
- Replies: 4
- Forum: General Math
-

Graduate This hypothesis is right about operators on convergent and divergent series?
Sorry for the bad English , do not speak the language very well. I posted this to know if the statement or " hypothesis " is correct . thank you very much =D. First Image:https://gyazo.com/7248311481c1273491db7d3608a5c48e Second Image:https://gyazo.com/d8fc52d0c99e0094a6a6fa7d0e5273b6 Third... -

Graduate Eigenfunction of multiple operators simultaneously?
Hello, I am taking an introductory course in quantum mechanics. One thing I am confused about is, Schrödinger's equation seems to be regarded as the "ultimate" formula which determines a particle's possible wavefunctions and energies, given a certain potential (Hamiltonian of psi = Energy...- JaredMTg
- Thread
- Eigenfunction Multiple Operators
- Replies: 4
- Forum: Quantum Physics
-
C
Graduate Projection operators and Weyl spinors
I am working through some course notes where the aim is to derive the equations of motion satisfied by the left handed and right handed components of the Dirac spinor ##\psi##. From the Dirac lagrangian, we have $$\mathcal L = \bar \psi (i \not \partial P_L - m P_L)\psi_L + \bar \psi (i \not...- CAF123
- Thread
- Operators Projection Spinors Weyl
- Replies: 6
- Forum: High Energy, Nuclear, Particle Physics
-
S
MHB Do Commuting Linear Integral Operators Share Eigenfunctions and Eigenvalues?
I have two linear integral operators $Ky=\int_{a}^{b} \,k(x,s)y(s)ds$ $Ly=\int_{a}^{b} \,l(x,s)y(s)ds$ their kernels commute Do they have same eigenfunctions like matrices and for instance in this case their product is the product of their eigenvalues. I am poorly read in operator theory...- sarrah1
- Thread
- Operators
- Replies: 1
- Forum: Topology and Analysis
-
I
Hermitian adjoint operators (simple "proofs")
Homework Statement I'm having some trouble with questions asking me to "show" or "prove" instead of computing an answer so I'm looking for some input if I'm actually doing what I'm supposed to or not (and for the last one I don't know where to get started really.) 1. Show that ##T^*## is...- Incand
- Thread
- Hermitian Operators Proofs
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
I
Self adjoint operators, eigenfunctions & eigenvalues
Homework Statement Consider the space ##P_n = \text{Span}\{ e^{ik\theta};k=0,\pm 1, \dots , \pm n\}##, with the hermitian ##L^2##-inner product ##\langle f,g\rangle = \int_{-\pi}^\pi f(\theta) \overline{g(\theta)}d\theta##. Define operators ##A,B,C,D## as ##A = \frac{d}{d\theta}, \; \; B=...- Incand
- Thread
- Eigenfunctions Eigenvalues Operators Self
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
S
Graduate Ladder operators in Klein -Gordon canonical quantisation
The quantum Klein-Gordon field ##\phi({\bf{x}})## and its momentum density ##\pi({\bf{x}})## are given in Fourier space by ##\phi({\bf{x}}) = \int \frac{d^{3}p}{(2\pi)^{3}} \frac{1}{\sqrt{2 \omega_{{\bf{p}}}}} \big( a_{{\bf{p}}} e^{i{\bf{p}} \cdot {\bf{x}}} + a^{\dagger}_{{\bf{p}}}...- spaghetti3451
- Thread
- Klein Ladder operators Operators Quantisation
- Replies: 5
- Forum: Quantum Physics
-

Graduate Spin Operators: Axial for QM, Polar in Clifford Algebra?
Hello folks! New to this forum, so hoping I'm not retreading old ground. The Pauli matrices are spin angular momentum operators in quantum mechanics and thus are axial vectors. But in Clifford algebra in three dimensions they are odd basis elements and thus polar vectors. Hestenes, Baylis, other...- Elemental
- Thread
- Algebra Axial Clifford algebra Operators Polar Qm Spin
- Replies: 7
- Forum: Quantum Physics
-
Graduate Superselection rules and non-observable Hermitian operators
Its usually said(like https://en.wikipedia.org/wiki/Superselectiond ) that superselection rules imply that not all Hermitian operators can be considered to be physical observables. But I don't understand how that follows. Can someone explain? Thanks- ShayanJ
- Thread
- Hermitian Operators Rules
- Replies: 4
- Forum: Quantum Physics
-
A
Graduate Operators implementation with operators
Hello I may make some mistakes because I am not professional at physics:smile:.So I want to know how to implementate wave function with operators example:p(hat) impletated with ψ so: p(hat)ψ=pψ so as you saw it was momentum operator and momentum operator is:-iħ∂/∂x as you saw it is one...- AleksanderPhy
- Thread
- Operators
- Replies: 4
- Forum: Quantum Physics
-

Operators and eigenstates/values
Homework Statement Let the Hermitian operator A^ corresponding to the observable A have two eigenstates |a1> and |a2> with eigenvalues a1 and a2, respectively, where a1 ≠ a2. Show that A^ can be written in the form A^ = a1|a1><a1| + a2|a2><a2|. Homework EquationsThe Attempt at a Solution I...- nmsurobert
- Thread
- Operators
- Replies: 4
- Forum: Advanced Physics Homework Help
-
G
Graduate How Fourier components of vector potential becomes operators
Hello. I'm studying quantization of electromagnetic field (to see photon!) and on the way to reach harmonic oscillator Hamiltonian as a final stage, sudden transition that the Fourier components of vector potential A become quantum operators is observed. (See...- goodphy
- Thread
- Components Electromagnetic field Fourier Fourier decomposition Hamiltonian Harmonic oscillator Operators Photon Potential Quantization Vector Vector potential
- Replies: 1
- Forum: Quantum Physics
-

Graduate Questions about operators and commutators
so I have an expression here: [P,g(r)]= -ih dg/dr P is the momentum operator working on a function g(r). Is this true because when you expand the left hand side the expression g(r)P is zero because the del operator has nothing to work on?- maverick_76
- Thread
- Commutators Operators
- Replies: 6
- Forum: Calculus
-

Graduate Ladder operators and matrix elements...
Please I need your help in such problems.. in terms of ladder operators to simplify the calculation of matrix elements... calculate those i) <u+2|P2|u> ii) <u+1| X3|u> If u is different in both sides, then the value is 0? is it right it is 0 fir both i and ii? when exactly equals 0, please...- Activeuser
- Thread
- Elements Ladder operators Matrix Operators
- Replies: 7
- Forum: Quantum Physics
-
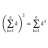
Microcanonical partition function - Dirac delta of operators
Homework Statement Why is it that the microcanonical partition function is ##W = Tr\{\delta(E - \hat{H})\}##? As in, for example, Mattis page 62? Moreover, what's the meaning of taking the Dirac delta of an operator like ##\hat{H}##? Homework Equations The density of states at fixed energy is...- ddd123
- Thread
- Delta Dirac Dirac delta Function Microcanonical ensemble Operators Partition Partition function Statistical mechanics
- Replies: 2
- Forum: Advanced Physics Homework Help