Frequently Made Errors in Mechanics: Hydrostatics
Entire List for Frequently Made Errors Series
Table of Contents
1. Archimedes’ Principle
X “When a body is placed in a liquid, the weight of the body equals the weight of the liquid displaced”
That will only be true if the body is floating. Here’s what Archimedes wrote:
✓ “Any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.”
But what does displacement mean here?
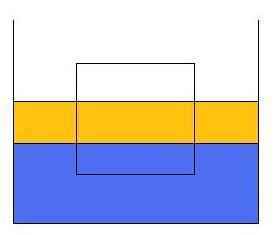
Example: An egg of volume 50mL is placed in a narrow cup. 40mL of water is poured in. What is the maximum possible buoyant force on the egg? Use ##g = 10m/s^2##”
Attempted answer:
X There are only 40mL of water, so there can’t be more than 40mL displaced. The maximum buoyant force is 0.4 N.
If the space around the egg, up to the egg’s height in the cup, is less than 40mL then the egg may be completely covered. The displacement is the volume of the egg below the surface of the water, so it may be as much as 50mL.
Example: “A cube of mass m and height a floats upright in a tank containing water density ##\rho_w## and oil density ##\rho_o##. If the height of the top of the cube above the oil is h, how high is it above the oil/water boundary?”
The challenge is to figure out the displaced volume of each fluid.
Imagine removing the solid body, leaving a cavity which the fluids would flow back into.
The displaced bodies of fluid are what would be needed to fill the cavity in such a way that the fluid already present would stay put.
If you were to insert the additional fluid such that some part of the cavity below the oil/water boundary contained oil, that would not be stable.
Similarly, any fluid above that boundary, or any oil below the oil/water boundary, and so on. There is only one stable arrangement:
If the top of the cube is height y above the oil/water boundary then the volume of water displaced is ##a^2(a-y)## and the volume of oil displaced is ##a^2(y-h)##.
2. Archimedes versus pressure integral
“A cube side a, weight W, sits on the flat bottom of a tank of water depth h>a. A cable attached to the top of the block is used to raise the block. What force is needed to lift it off the bottom?”
Attempted answer using pressures:
The pressure on the top of the block is ##\rho_whg+P_{atm}##, exerting a downward force ##(\rho_whg+P_{atm})a^2##. The forces on the sides of the cube cancel. On the point of leaving the floor of the tank there is no normal force.
✓?X? Tension in cable = ##W+(\rho_w(h-a)g+P_{atm})a^2 = W+(\rho_whg+P_{atm})a^2 -\rho_wVg##.
Attempted answer using Archimedes’ Principle:
✓?X? Tension in cable = ##W-\rho_wVg##.
Either could be correct! It depends on whether the underside of the cube makes such perfect contact with the floor of the tank that there is no water or air between. It is the same principle as a rubber suction cup.
However, that is unlikely, so we should assume a thin layer of water under the cube. This produces an upward force ##(\rho_whg+P_{atm})a^2##, yielding the same net force as given by Archimedes’ Principle.
The buoyant force could be determined by a surface integral of the pressure: ##\int_S \rho g |z|.\vec{dA}##, where |z| is the depth, S is the surface, and ##\vec{dA}## is the area element vector over S. Since the integrand is a vector, some cancellation will occur in the integration. Clearly, this could prove a difficult integral on some surfaces. This demonstrates the power of Archimedes’ Principle.
3. Stability
“A cylindrical beaker of mass m, radius r, and negligible wall thickness, has its center of gravity height h above its base. To what depth should it be filled with water so as to make it as stable as possible?”
Given answer:
X “for maximum stability the overall center of gravity must be as low as possible; that will be when it is at the water surface”
The second statement is correct, but not the first.
In general, stability can be defined in various ways. E.g., the strength of resistance (restorative force or torque) to a small perturbation. With that definition, maximum stability will be with a full beaker.
The ‘lowest centre of gravity’ answer typically corresponds to a definition of stability based on the degree of perturbation (specifically, tilt angle) required to make it unstable. However, that only works for solid objects. When the beaker is tilted, the contents will shift. At the point of instability, the water will occupy a more complicated region. (Particularly complicated if it no longer covers the base of the beaker.)
Masters in Mathematics. Interests: climate change & renewable energy; travel; cycling, bushwalking; mathematical puzzles and paradoxes, Azed crosswords, bridge


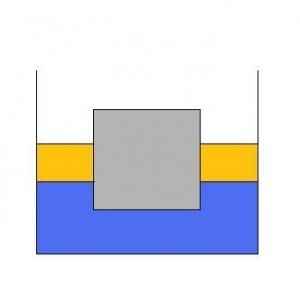
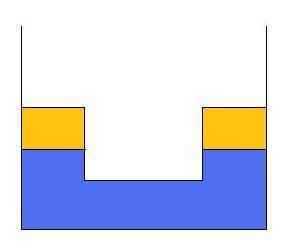
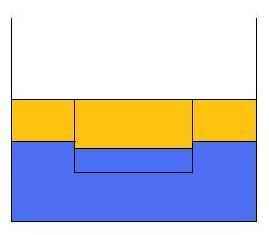






Qestion 2 is interesting as an example of how one could go into more and more detail into the phenomenon and get different answers for each “level” of detail. This is particularly true here because we ask about the force at the very instant when the block is about to move upward. In practice, there would be no “instant” but there would be a transient process where the force would vary in interesting ways before settling down into ##W-rhoVg##
If we apply an increasing upward force on the rope, a moment would come when water would try to rush into the gap between the block and the floor. You could think of it as a transient partial vacuum under the block, or as a bernoulli pressure drop that results in a net downward component.
If the slack on the rope is taken up infinitely slowly, then the bernoulli / vacuum effect would always be negligible and the tension would climb smoothly from zero to the archimedes value.
[USER=334404]@haruspex[/USER] is really on a roll with these tutorials. Soon I will be linking them all together.
Qestion 2 is interesting as an example of how one could go into more and more detail into the phenomenon and get different answers for each "level" of detail. This is particularly true here because we ask about the force at the very instant when the block is about to move upward. In practice, there would be no "instant" but there would be a transient process where the force would vary in interesting ways before settling down into ##W-\rhoVg##If we apply an increasing upward force on the rope, a moment would come when water would try to rush into the gap between the block and the floor. You could think of it as a transient partial vacuum under the block, or as a bernoulli pressure drop that results in a net downward component. If the slack on the rope is taken up infinitely slowly, then the bernoulli / vacuum effect would always be negligible and the tension would climb smoothly from zero to the archimedes value.