How Quantum Information Theory Solves “the only mystery” of Quantum Mechanics

In Chapter 37 of “The Feynman Lectures on Physics Volume 1,” Richard Feynman famously wrote that the mystery of wave-particle duality in the double-slit experiment is:

a phenomenon which is impossible, absolutely impossible to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by “explaining” how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics.

In this Insight, I want to show you how Brukner and Zeilinger’s information-theoretic principle of Information Invariance & Continuity as justified by the relativity principle solves this mystery. In How Quantum Information Theorists Revealed the Relativity Principle at the Foundation of Quantum Mechanics, I explained how Information Invariance & Continuity entails that everyone measures the same value for Planck’s constant h, regardless of the relative spatial orientation of their inertial reference frames. Obviously, that can be justified by the relativity principle, i.e., the laws of physics (including their constants of Nature) are the same in all inertial reference frames, which I call “no preferred reference frame (NPRF).” While it is commonly assumed that different inertial reference frames are only related by different relative velocities, they are in fact also related by different relative spatial orientations, spatial locations, and temporal locations. The entire set of transformations between such reference frames that guarantees everyone will measure the same value for the speed of light c (the light postulate of special relativity), is the set of Poincare transformations, i.e., Lorentz boosts, spatial rotations, spatial translations, and time translations. The light postulate is justified by the relativity principle and special relativity (SR) follows from that fact, so I will characterize SR as following from NPRF + c. Likewise, the axiomatic reconstructions of QM based on information-theoretic principles show how one can derive the (finite-dimensional) Hilbert space of QM from Information Invariance & Continuity, which can be justified by NPRF, so I will characterize QM as following from NPRF + h.

The axiomatic reconstructions of QM based on information-theoretic principles render QM a principle theory, as I explained in A Principle Explanation of the “Mysteries” of Modern Physics. In general, a principle explanation solving some mystery can be written:

Compelling fundamental principle $\rightarrow$ Justifies empirically discovered fact $\rightarrow$ Dictating the mystery

In this case, we have:

Relativity principle $\rightarrow$ Justifies Information Invariance & Continuity $\rightarrow$ Dictating wave-particle duality for the double-slit experiment

Recall from “How Quantum Information Theorists Revealed …” for the spin-$\frac{1}{2}$ particle, Information Invariance & Continuity entails that everyone measures the same value for h regardless of the orientation of their Stern-Gerlach (SG) magnets, i.e., regardless of the spatial orientation of their inertial reference frames. Since we’re talking about a constant of Nature having the same value in all inertial reference frames (related in this case by spatial rotations), this empirically discovered fact can be justified by NPRF. To see how the classical formalism follows on average from the quantum formalism, I showed how the classical constructive account predicts that the atomic (magnetic) dipoles along $\hat{z}$ should be deflected by $\cos{\left(\theta \right)}$ when they pass through SG magnets oriented at $\hat{b}$ making an angle $\theta$ with $\hat{z}$. Instead, we find only full deflections of $\pm 1$ $\left(\pm \frac{\hbar}{2}\right)$ along $\hat{b}$ that average to $\cos{\left(\theta \right)}$. This gives you ‘average-only’ projection of spin angular momentum between these reference frames as a consequence of NPRF + h.

For polarization, Information Invariance & Continuity entails that everyone measures the same value for h regardless of the orientation of their polarizing filter, i.e., regardless of the spatial orientation of their inertial reference frames, which is easily justified by NPRF just like the spin-$\frac{1}{2}$ particle. The empirically discovered fact in this case is that a photon either passes or it doesn’t pass through a polarizing filter, i.e., there are no ‘partial photons’ passed by a polarizer. We can say that our empirically discovered fact in this case results because $E = hf$ and if a fractional photon passed through a polarizer, the value of h would be reduced by that fraction, so you would have two inertial reference frames related by a spatial rotation whereby h had two different values in violation of NPRF. This gives you ‘average-only’ transmission of polarized electromagnetic energy between these reference frames as a consequence of NPRF + h. In this case, the classical wave mechanics follows on average from the distribution of photon (particle) energy per quantum mechanics. Now let’s provide a similar NPRF + h solution to the mystery of wave-particle duality in the double-slit experiment.

Our experimental context will be established by equally illuminating a pair of slits in phase with a laser of wavelength $\lambda$, then reducing the intensity of the laser until it is emitting one photon at a time (Figure 1); this is our quantum bit of information aka qubit (physical instantiation of 2-dim Hilbert space). The type of measurement we do on this qubit will be established by where we choose to locate the detector behind the slits. When we place the detector right up against the slits we are doing a ‘which-slit’ or ‘position’ measurement (Figure 2). Since the slits are equally illuminated, each photon has a 50% chance of hitting the detector behind Slit 1 and a 50% chance of hitting the detector behind Slit 2. Thus, we can write the state of our qubit in terms of the ‘which-slit’ measurement outcomes as 50% Slit 1 + 50% Slit 2. If we locate the detector far from the slits (compared to the slit separation), we are doing an ‘interference’ or ‘momentum’ measurement (Figure 3); an interference pattern allows us to obtain a wavelength $\lambda$ whence momentum $p = \frac{h}{\lambda}$. Since every photon lands in a band of constructive interference in this measurement, we can write our qubit state in terms of the ‘interference’ measurement as 100% Constructive. The classical understanding of electromagnetic radiation would say that the momentum of $p = \frac{h}{\lambda}$ should be split evenly between the two slits and the screen surrounding the slits. But that would mean we would obtain momentum of less than $p = \frac{h}{\lambda}$ on our detector, which means we have a fractional value of h in our measurement (the wavelength doesn’t change). Since we must always measure h, never a fraction of h, we observe quanta of momentum, i.e., “particle-like” behavior called photons, that behave like waves ‘collectively’ in the ‘interference’ measurement. Notice that in the double-slit experiment, the measurement configurations change according to spatial translations.

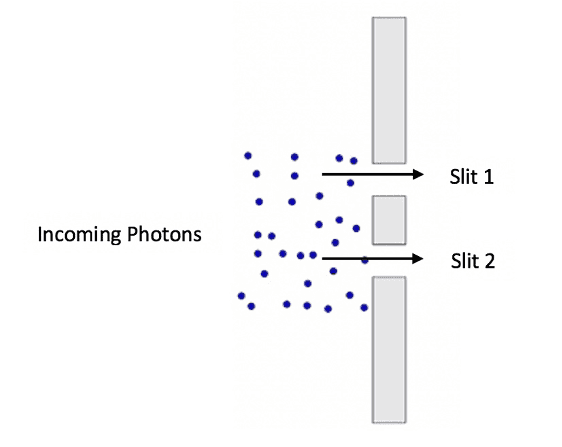
Figure 1. The double-slit qubit. Image adapted from: Physics in a minute: The double slit experiment. https://plus.maths.org/content/physics-minute-double-slit-experiment-0

 

 

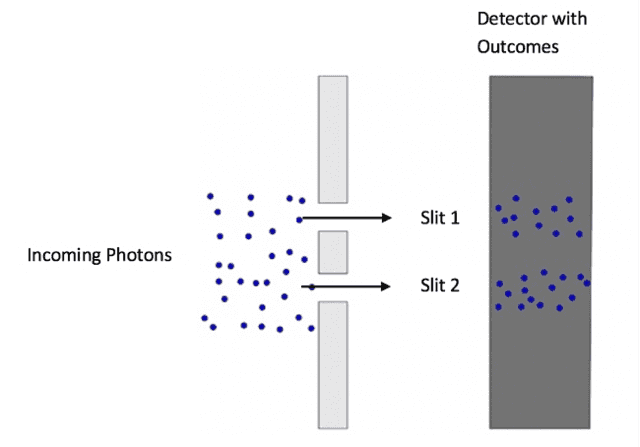
Figure 2. ‘Which-slit’ measurement for the double-slit qubit. Detector Immediately Behind Slits. Image adapted from: Physics in a minute: The double slit experiment. https://plus.maths.org/content/physics-minute-double-slit-experiment-0

 

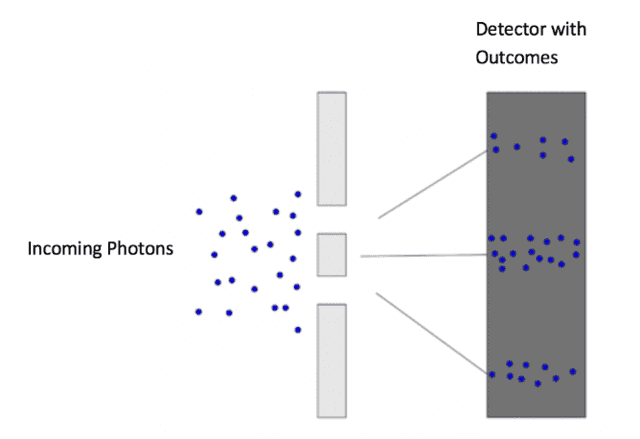
Figure 3. ‘Interference’ measurement for the double-slit qubit. Detector Far Behind Slits. Image adapted from: Physics in a minute: The double slit experiment. https://plus.maths.org/content/physics-minute-double-slit-experiment-0

Now let’s see how this entails quantum superposition (whence quantum entanglement) and complementarity. The Slit 1 image region on the detector is above center and the Slit 2 image region is below center on the detector (Figure 2), so the outcomes for a ‘which-slit’ measurement that are above center are 100% associated with Slit 1, while those that are below center are 100% associated with Slit 2 (yes, that’s trivial because the detector is placed right up against the slits). This measurement gives the position (in terms of ‘which slit’) exactly but says nothing about its “complementary” property of momentum (given by wavelength). As you move the detector continuously farther and farther away from the slits, the probability that a photon detection above center is associated with Slit 2 gradually increases from 0% until the detector gets to the ‘interference’ measurement location (Figure 3) where the probability that a photon detection event above center is associated with Slit 2 is 50%. Same with Slit 1 below center. That is, a photon detection event for the ‘interference’ measurement above center is equally likely to be associated with Slit 2 as Slit 1 (vice versa for below center).

This ‘interference’ measurement totally randomizes the ‘position’ information that the complementary ‘which-slit’ measurement provides, but the geometry of the ‘interference’ measurement and outcome allows you to compute a precise value of wavelength and that allows for an exact value for momentum. Quantum superposition and complementary measurements for a qubit are not at all mysterious when you see what they mean physically – the invariant information obtainable from a qubit in different measurement configurations is just different information.

So, the invariant information of the qubit from NPRF + h is manifested in the double-slit experiment as follows. There are two equally likely outcomes (photon behind Slit 1 or photon behind Slit 2) in the ‘which-slit’ measurement configuration and this distribution changes continuously to one definite outcome (100% probability that a photon will land in the constructive interference pattern) in the ‘interference’ measurement configuration as the detector is moved continuously from the ‘which-slit’ configuration to the ‘interference’ configuration. This explanation of the double-slit experiment per NPRF + h and the qubit shows that Feynman was essentially correct. The mystery of the double-slit experiment resides in the fact that NPRF + h demands we obtain quanta of momentum $p = \frac{h}{\lambda}$ rather than a continuum of wave intensity as in electromagnetism. However, the quantum measurement context is that for momentum p, so an interference pattern allowing us to compute $\lambda$ for use in $p = \frac{h}{\lambda}$ is required. Therefore, the interference pattern per classical wave mechanics is what must obtain on average (collectively) in this quantum mechanics context. That is, the mystery of wave-particle duality in the double-slit experiment follows from the fact that the quantum case doesn’t conform to the classical case of particles or the classical case of waves, but must be a combination of both due to NPRF + h. In all three examples, NPRF + h demands that a classically continuous quantity (angular momentum, polarization, momentum) be quantized, so that you have to take an average to recover the classical continuity. That is how quantum information theory’s principle of Information Invariance & Continuity, as justified by the relativity principle, solves what Feynman called “the only mystery” of QM in principle fashion.