Mutual Inductance: When k≠1 and Two Coupling Coefficients

Mutual inductance and the coupling coefficient

A commonly used formula for mutual inductance M between two nearby coils L₁ and L₂ is M = k√(L₁*L₂). This formula, however, assumes equal percentage flux linkages between the two coils. That requirement is often omitted in several references.

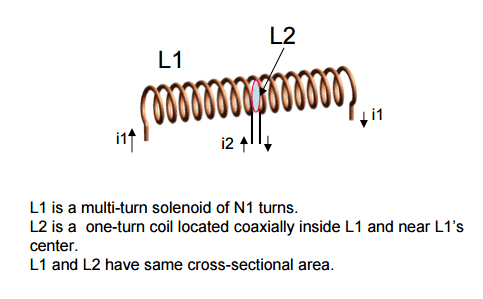
Example: single-turn coil inside a long solenoid (Fig. 1)

This requirement is not necessarily met, as shown in Fig. 1. Consider a single-turn coil L₂ embedded within a long solenoid L₁ with N₁ turns. Flux from L₁ essentially completely links L₂, whereas flux from L₂ couples only partially into L₁.

Some nomenclature:

• φ₁₁ = flux generated by L₁ coupling into itself;
• φ₂₁ = flux generated by L₁ coupling into L₂;
• φ₁₂ = flux generated by L₂ coupling into L₁;
• φ₂₂ = flux generated by L₂ coupling into itself.

Nomenclature and basic relations

So mutual inductance M₂₁ = φ₂₁/i₁ (N₂ = 1 here); and M₁₂ = N₁φ₁₂/i₂.

L₁ = N₁φ₁₁/i₁

L₂ = φ₂₂/i₂.

Symmetry and a common fallacy

As is well known, M₂₁ = M₁₂ = M. (The proof is nontrivial; Feynman uses the magnetic vector potential while Skilling invokes an energy argument.)

The following fallacious reasoning can ensue — I speak from experience. Since M can be computed either way above, it seems easier to use M₂₁ because φ₂₁ = φ₁₁. I won’t derive the result here; in vacuum one finds M = μ₀A/l, where A is the common cross-sectional area and l is the length of L₁.

From that you might conclude there is 100% flux coupling between L₁ and L₂, set k = 1, and write M = k√(L₁L₂). This conclusion is incorrect.

Why k = 1 is not generally valid

If that reasoning were valid, we could deduce L₂ from known L₁ and M alone. But L₂ actually depends on both the common area A and the wire radius R and generally requires evaluating a specialized integral. The fallacious computation would imply that L₂ is a function of L₁ even when i₁ = 0, and would ignore physical realities such as L₂ → ∞ as R → 0.

Two distinct coupling coefficients

The resolution is that there are really two coupling coefficients. Define

• k₁ = φ₂₁/φ₁₁
• k₂ = φ₁₂/φ₂₂

With the relations above one finds

M = √(k₁k₂L₁L₂).

The bottom line is that we typically know k₁ (for example, from the solenoid flux linking the small coil) and L₁ but not k₂ or L₂. There is a single coupling coefficient k = k₁ = k₂ if and only if the fraction of flux from one coil coupling into the other is the same for both coils.

---

When both coils are solenoids

Even if the single-turn coil were replaced by another long solenoid L₂, but of different length and wrapped on top of L₁ so that A is the same for both, there are still two different coupling coefficients involved. In that case the familiar relation L₂/L₁ = (N₂/N₁)² does not generally hold.

Further reading

Read my next article: https://www.physicsforums.com/insights/brachistochrone-subway/