Are Electromagnetic Waves Always Transverse? Full Explanation
In this insight, we will explore classical electrodynamics and examine whether electromagnetic (EM) waves are always transverse. We use Jefimenko’s equations and Poynting’s Theorem and conclude:
- EM waves are always transverse by the weak definition, where the fields are perpendicular to the propagation vector.
- EM waves are not always transverse by the strong definition, where we also require the E and B fields to be perpendicular to each other.
For what follows, we’ll assume the region of interest is vacuum. Similar conclusions generally hold for linear, isotropic, nondispersive materials. This assumption simplifies the relation between fields and the Poynting vector.
We also assume there are no boundaries (for example, waveguide walls) that impose special conditions on the fields and can cause the propagation direction to differ from the Poynting-vector direction.
Table of Contents
1. Fields perpendicular to the direction of propagation
Looking at Jefimenko’s equations — the general solution to Maxwell’s equations for arbitrary charge and current densities — we have:
$$\mathbf{E}(\mathbf{r},t)=\frac{1}{4\pi\epsilon_0}\int \left [\frac{\mathbf{r-r’}}{|\mathbf{r-r’}|^3}\rho(\mathbf{r’},t_r)+\frac{\mathbf{r-r’}}{|\mathbf{r-r’}|^2}\frac{1}{c}\frac{\partial\rho(\mathbf{r’},t_r)}{\partial t}-\frac{1}{c^2}\frac{1}{|\mathbf{r-r’}|}\frac{\partial \mathbf{J}(\mathbf{r’},t_r)}{\partial t}\right ]d^3\mathbf{r’}$$
$$\mathbf{B}(\mathbf{r},t)=-\frac{\mu_0}{4\pi}\int \left [ \frac{\mathbf{r-r’}}{|\mathbf{r-r’}|^3}\times\mathbf{J}(\mathbf{r’},t_r)+\frac{\mathbf{r-r’}}{|\mathbf{r-r’}|^2}\frac{1}{c}\times\frac{\partial \mathbf{J}(\mathbf{r’},t_r)}{\partial t}\right ]d^3\mathbf{r’}$$
Poynting vector and transversality
At first glance, those integrals do not immediately reveal the propagation direction of the ##\mathbf{E}## and ##\mathbf{B}## fields. However, Poynting’s theorem helps: the usual physical definition of a wave’s propagation direction is the direction of energy flow. For an electromagnetic field the energy flux is the Poynting vector ##\mathbf{S}=\mathbf{E}\times\mathbf{B}##.
Using the vector triple-product and properties of the cross product, one obtains
$$\mathbf{E}\cdot \mathbf{S}=(\mathbf{E}\times\mathbf{E})\cdot \mathbf{B}=0$$
and similarly for ##\mathbf{B}##. Therefore ##\mathbf{E}## and ##\mathbf{B}## are both perpendicular to ##\mathbf{S}##. In this weak sense — perpendicular to the propagation (energy-flow) vector — an EM wave is always transverse:
$$\mathbf{E}\perp\mathbf{S},\qquad \mathbf{B}\perp\mathbf{S}.$$
2. Fields perpendicular to each other?
Can we prove that ##\mathbf{E}## and ##\mathbf{B}## are always perpendicular to each other (the strong definition)? In the general case, we cannot. Although the integrands in Jefimenko’s equations may look locally orthogonal — for example, the term
$$\frac{1}{c^2}\frac{1}{|\mathbf{r-r’}|}\frac{\partial \mathbf{J}(\mathbf{r’},t_r)}{\partial t}$$
from the E-field integrand appears perpendicular to
$$\frac{\mathbf{r-r’}}{|\mathbf{r-r’}|^2}\frac{1}{c}\times\frac{\partial \mathbf{J}(\mathbf{r’},t_r)}{\partial t}$$
from the B-field integrand, orthogonality need not survive the integration. In general, the dot product of two vector integrals is not equal to the integral of the dot product:
$$\text{If }\mathbf{A}\cdot\mathbf{B}=0\text{ pointwise, it does not imply }\int\mathbf{A}\,dV\cdot\int\mathbf{B}\,dV=\int\mathbf{A}\cdot\mathbf{B}\,dV=0.$$
Thus nothing in the general Jefimenko form guarantees ##\mathbf{E}\cdot\mathbf{B}=0## everywhere.
Far-field (radiation-zone) approximation
To make progress, we often use the far-field (radiation-zone) approximation. Place the origin inside the source volume V (the region where ##\rho## and ##\mathbf{J}## are nonzero), assume the source is finite, and evaluate the fields at points ##\mathbf{r}## such that
$$|\mathbf{r}|\gg|\mathbf{r’}|\quad\text{for all }\mathbf{r’}\in V.$$
Then to leading order one may approximate
$$\frac{\mathbf{r-r’}}{|\mathbf{r-r’}|^i}\approx\frac{\mathbf{r}}{|\mathbf{r}|^i}.$$
This moves the common geometric factors outside the integrals (integration is over ##\mathbf{r’}##), and Jefimenko’s equations reduce to:
$$\mathbf{E}(\mathbf{r},t)=\frac{1}{4\pi\epsilon_0}\left [\frac{\mathbf{r}}{|\mathbf{r}|^3}\int \rho(\mathbf{r’},t_r) \,d^3\mathbf{r’}+\frac{\mathbf{r}}{c|\mathbf{r}|^2}\int\frac{\partial \rho(\mathbf{r’},t_r)}{\partial t}\, d^3\mathbf{r’}-\frac{1}{c^2|\mathbf{r}|}\int\frac{\partial \mathbf{J}(\mathbf{r’},t_r)}{\partial t}\,d^3\mathbf{r’}\right ]$$
$$\mathbf{B}(\mathbf{r},t)=-\frac{\mu_0}{4\pi}\left [ \frac{\mathbf{r}}{|\mathbf{r}|^3}\times \int \mathbf{J}(\mathbf{r’},t_r)\,d^3\mathbf{r’}+\frac{\mathbf{r}}{|\mathbf{r}|^2}\times \int \frac{\partial \mathbf{J}(\mathbf{r’},t_r)}{\partial t}\,d^3\mathbf{r’}\right ]$$
These expressions are valid only in the far-field region (not near the sources). Under this approximation, and with the additional assumption that time derivatives of the current do not change its direction (i.e. ##\partial\mathbf{J}/\partial t\parallel\mathbf{J}##), one can show that ##\mathbf{E}\cdot\mathbf{B}=0## in the radiation zone. That is, far from the source the radiated fields are orthogonal to each other and to the propagation direction.
3. Conclusions
Using Poynting’s theorem we have shown that the electric and magnetic fields are always perpendicular to the direction of energy flow (the Poynting vector). In this weak sense, EM waves are always transverse.
However, in the general near-source case the electric and magnetic fields need not be perpendicular to each other. Orthogonality of ##\mathbf{E}## and ##\mathbf{B}## arises in the far-field (radiation zone) under the usual approximations.
Thus, far from a finite source, an EM wave is fully transverse regardless of the detailed charge and current distributions that generated it (provided the source is finite and the far-field approximations apply).

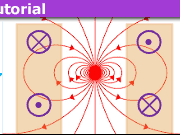







This is way more subtle! There is a century-old debate about Minkowski vs. Abraham and which is the right energy-current density or the momentum density of the em. field in polarizable media. The resolution is very salomonic: Both approaches are correct describing the canonical vs. the kinetic momentum of the field, and which one you have to consider depends on the situation you want to describe. See, e.g.,
[URL]https://doi.org/10.1098/rsta.2009.0207[/URL] (open access!)
Yes it is true that if we want to answer directly the question of the article then the answer is NO, electromagnetic waves are NOT always transverse(with either the weak or the strong notion).
However given that the medium of propagation is the vacuum (or any linear, isotropic and non dispersive medium where the Poynting vector gets the nice form $$\mathbf{S}=\mathbf{E}\times\mathbf{H}=\mathbf{E}\times\frac{1}{\mu}\mathbf{B}$$) and also given that there are no boundaries (I ll edit the insight and add this condition as [USER=192203]@jasonRF[/USER] notes) then the fields are perpendicular to the direction of propagation, and furthermore in the far region they are perpendicular to each other.
”
Great article but I believe it should be made more explicit the fact that it refers to a restricted case.
Given the fact that there are many exceptions, the wording (“fields are always perpendicular to the direction of propagation”) is misleading. Especially for such students who are too easily inclined to memorize a statement without a care about the conditions of valability of that statement. As the title does not specify any conditions, the answer should be definitely “NO”.
”
Yes – when I saw the title I was [i]assuming[/i] the answer would be NO… The author lists some of the restrictions at the top of the article, but perhaps could add that they are also assuming there are no boundaries. Delta2 is of course dealing with the most important cast (in my opinion), if not the most general.
”
Also, in waveguides you can have modes where only the electric or magnetic fields are transverse. For TE mode, there is no electric component in the direction of propagation. For a TM mode, there is no magnetic field in the direction of propagation and for a TEM mode both the E and H fields are transverse, TEM modes cannot be supported in a hollow waveguide. Those are what you get in coax cable.
”
Yes in waveguides there are boundary conditions imposed on the E,B fields that make the direction of propagation different than the direction of the Poynting vector. In this article we assumed that there are no boundary conditions imposed on the fields and that the propagation direction coincides with the direction of energy flow.
I believe in the waveguide case, the Poynting vector has one major component along the direction of propagation, and one smaller component perpendicular to the propagation direction, which represents a small fraction of energy that is trapped between the walls of the waveguide.
Great article, but of course this is for vacuum E&M only. In matter you can have” plasma waves”! A nice summary is here:
[URL]https://en.wikipedia.org/wiki/Waves_in_plasmas[/URL]