Transformation Definition and 1000 Threads
-
M
Undergrad What Is the Amplitude of a Harmonic Load in the Frequency Domain?
Hello, I am having a bit of trouble with calculating the Fourier transformation of a harmonic load. I have the function f(t) = A * sin(ωt) in the time-domain. I would like to represent this function in the frequency domain. What would be its amplitude? Thank you -
M
Graduate Linear Algebra; Transformation of cross product
Pre-knowledge A matrix is a linear transformation if, T(u+v)= T(u) +T(v) and T(cu)=cT(u). Theorem 8.4.2 If V is a finnite dimensional vector space, and T: V-> V is a linear operator then the following are equivalent. a) T is one to one, b) ker(T)=0, c)...- Myr73
- Thread
- Algebra Cross Cross product Linear Linear algebra Product Transformation
- Replies: 59
- Forum: Linear and Abstract Algebra
-
R
How frequency domain topic should be taught in the academic course?
This is a soft question but I think it's a real fact.The Frequency domain has made revolution in the field of Mathematics,Physics,Digital Signal and image Processing etc. Some of concepts which are very difficult to analyse in spatial or time domain can be very easily understood in the frequency...- ramdas
- Thread
- Academic Course Domain Fourier Frequency Frequency domain Topic Transformation
- Replies: 4
- Forum: STEM Educators and Teaching
-
S
Helmholtz Free Energy Legendre Transformation
Homework Statement Show how a Legendre transformation is used to obtain the Helmholtz free energy A(T,V) from the internal energy and derive the general expression for the differential of A. Homework Equations Internal Energy is a function of Entropy and Volume. U Ξ (S, V) A Ξ (T,V) A = U...- says
- Thread
- Energy Free energy Helmholtz Helmholtz free energy Legendre Legendre transformation Transformation
- Replies: 1
- Forum: Introductory Physics Homework Help
-
A
Linear Fractional Transformation - find the formula
http://math.sfsu.edu/federico/Clase/Math350.S15/linea.JPG 1. Homework Statement The picture below represents the map from a "green projective line" to a "red projective line." It takes the "green points" 1,3,7,-11 to the "red points" 0,6,10,20, respectively as shown by the ruler. Let f be the...- anniecvc
- Thread
- Formula fractional Linear Transformation
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
A
Graduate Hubbard Stratonovich transformation
Introducing the Hubbard Stratonovich transformation my book uses an expression for completeness that I don't understand (the one indicated on the picture). Can anyone explain why this is indeed unity?- aaaa202
- Thread
- Transformation
- Replies: 1
- Forum: Quantum Physics
-
W
Grade 11 Energy Transformation with External Forces
1. Question. A 15 kg child slides from rest, down a playground slide that is 4.0m long. The slide makes a 40degree angle with the horizontal. The child's speed at the bottom is 3.2 m/s. What was the force that the slide was exerting on the child? Answer: 75 N [up the slide] 2. My Attempt. Ek...- Wajeeha
- Thread
- Energy External forces Forces Grade 11 Transformation
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Graduate Lorentz Transformation Equations, time transformation
t' = γ(t - vx/c2) where t is the time in the stationary frame t' is the time in the moving frame v is the relative velocity between the two frames and x is the distance traveled in the time t in the stationary frame. ∴ x = vt substituting this into the Lorentz time equation gives us: t' = γt(1 -...- Grimble
- Thread
- Lorentz Lorentz transformation Time Transformation
- Replies: 46
- Forum: Special and General Relativity
-
E
Graduate Gauge transformation which counteract wave function
Gauge transformation can be written as: ##\psi(\vec{r},t)\rightarrow e^{-i \frac{e}{\hbar c}f(\vec{r},t)}\psi(\vec{r},t)## http://quantummechanics.ucsd.edu/ph130a/130_notes/node296.html Does it have any sense that we choose such function ##f##, that all right side is constant in time. Is this...- exponent137
- Thread
- Function Gauge Gauge transformation Transformation Wave Wave function
- Replies: 8
- Forum: Quantum Physics
-

Unknown Transformation Machine
Homework Statement You have a unknown Transformation machine T. that transforms from R^4 --> R^3 Vectors U and V are known and the output from T is also known. Can You calculate the values of T? Homework Equations [/B] What values/information is needed to calcuate T ?The Attempt at a...- JoelN
- Thread
- Machine Transformation
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-
K
Graduate Directional independence of motion in Lorentz Transformation
Hi All, I am trying to understand the directional independence of LT. In contrast, we all know that Doppler Effect is dependent on the direction of motion. I have tried to find any reasoning or explanation and could not find one so far. May be I did not use correct terms in my searches. If...- Kanesan
- Thread
- Independence Lorentz Lorentz transformation Motion Transformation
- Replies: 22
- Forum: Special and General Relativity
-

Graduate Legendre Transformation of Lagrangian density ?
Hi I began to study the basics of QED. Now I am studying Lagrangian and Hamiltonian densities of Dirac Equation. I'll call them L density and H density for convenience :)Anyway, the derivation of the H density from L density using Legendre transformation confuses me :( I thought because...- DOTDO
- Thread
- Density Lagrangian Lagrangian density Legendre Legendre transformation Transformation
- Replies: 2
- Forum: Quantum Physics
-
P
Graduate ##\bar{\psi}=e^{i\theta}\psi## global gauge transformation
Why is ##\bar{\psi}=e^{i\theta}\psi##, where ##\theta## is a real number, used as the global gauge transformation? Why ##e^{i \theta}##; what's the physical significance or benefit? Why is ##\bar{\psi} = e^{i \theta(x)} \psi## the local gauge transformation? What does ##\theta## being a...- PerilousGourd
- Thread
- Gauge Gauge theory Gauge transformation Global Transformation
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-

Inverse Laplace Transformation
Homework Statement Solve the following: $$\mathscr{L}_s^{-1} \left\{ \frac{s}{s^2-s+\frac{17}{4}} \right\}$$ Homework Equations Table of Laplace Transforms.The Attempt at a Solution The solution is $$f(t) = (1/4 )e^{t/2} (\sin(2 t)+4 \cos(2 t))$$ I know I need to break up ##F(s)## into...- END
- Thread
- Inverse Laplace Laplace transform Transformation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Problem with signs in the Lorentz Transformation equations
Homework Statement The following is Exercise 2.1 from from Ray d'Inverno's 'Introducing Einstein's Relativity.' (a) Write down the Galilean transformation from observer ##S## to observer ##S'##, where ##S'## has velocity ##v_1## relative to ##S##. (b) Find the transformation from ##S'## to...- spaghetti3451
- Thread
- Lorentz Lorentz transformation Transformation
- Replies: 4
- Forum: Introductory Physics Homework Help
-
S
Laplace transformation question
Trying to answer the question: x"+3x'+2x=u(t-1)+2(t-2)u(t-2), x(0)=1, x'(0)=-1 My book has the answer but I need to see how to solve a problem like this. Professor didn't have time to cover this section but he said one of these might be on the test. Any help is greatly appreciated.- sfgoat
- Thread
- Laplace Transformation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
Graduate Vector subspace and linear transformation
X ={(x1,x2,x2 −x1,3x2):x1,x2 ∈R} f(x1,x2,x2 −x1,3x2)=(x1,x1,0,3x1) 1. Find a basis for X. 2. Find dim X. 3. Find ker f and I am f 4. Find bases for ker f and I am f 5. Is f a bijection? Why? 6. Find a diagonal matrix for f. My attempt: 1. (1, 1, 0, 3) and (1, 2, 1, 6) 2. Dim X = 2 3. Ker f = 0...- Montgomery
- Thread
- Linear Linear algebra Linear transformation Subspace Transformation Vector
- Replies: 1
- Forum: Linear and Abstract Algebra
-
K
Transformation from Body-frame to ECEF-frame
Homework Statement I have a body which is instantiated on Earth at some latitude, longitude and altitude. The body has acceleration which is expressed in body coordinates and the acceleration can be integrated to obtain the velocity vector which is also expressed in body coordinates. ECI and...- Kuu
- Thread
- Body Transformation
- Replies: 3
- Forum: Introductory Physics Homework Help
-
J
Graduate Gauge Transformation Quantum Electrodynamics
It's well known when if we are working on problems related to particles in presence of an electromanetic field, the way we state the problem can be done using the next Hamiltonian: H=\dfrac{(p-\frac{e}{c}A)^2}{2m} +e \phi where the only condition for A is: \vec{\nabla } \times \vec{A} =\vec{B}...- Juan Carlos
- Thread
- Electrodynamics Gauge Gauge transformation Quantum Quantum electrodynamics Transformation
- Replies: 1
- Forum: Quantum Physics
-
I
How to Conclude -23.7 Corresponds to SigmaX' in Plane Stress Transformation?
When one substitutes the angle -23.7 into the plane stress transformation equation for SigmaX' you indeed get -46.42 MPa (as shown in the images). However, if you substitute this same angle into the plane stress transformation equation for SigmaY', you yield the other principal stress of 116.4...- influx
- Thread
- Plane Stress Transformation
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-

Graduate Tensor Density Transformation Law: Order of Jacobian Matrix?
I just have a quick question on which order around the numerator and denominator should be in the jacobian matrix that multiplies the expression. As in general Lecture Notes on General Relativity by Sean M. Carroll, 1997 he has the law as ## \xi_{\mu'_{1}\mu'_{2}...\mu'_{n}}=|\frac{\partial...- binbagsss
- Thread
- Density Law Tensor Transformation Transformation law
- Replies: 6
- Forum: Special and General Relativity
-
H
Graduate Transformation equation of velocity contradicts stellar aberration?
Let S be the frame where the Sun is at rest. Imagine light from the North Star reaches the centre of the Sun, and let's define the equatorial plane as the plane that is perpendicular to this light and cuts the Sun into two hemisphere. Suppose a distant star A is on this equatorial plane and its...- Happiness
- Thread
- Aberration Contradiction Stellar Transformation Velocity Velocity transformation
- Replies: 11
- Forum: Special and General Relativity
-
H
Graduate Proof of Transformation Equation for Electric Field Ex
I want to prove that the transformation equation for electric field holds, namely Ex = Ex', where Ex is the x component of E field in S frame and Ex' is that in S' frame, for the special case in which the charged particle has a vertical velocity Uy' in the S' frame (Ux' = Uz' = 0). It is already...- Happiness
- Thread
- Electric Electric field Field Proof Special relativity Transformation
- Replies: 7
- Forum: Special and General Relativity
-
R
Undergrad Transformation rules in Boolean algebra
I know De-Morgan's law that $$ -(p∧q) = -p∨-q $$ Also $$ -(p∨q) = -p∧-q $$ But for material implication and bi conditional operations there are also some transformation. What is the law or proof for it? Like $$ p⇒q = -p∨q $$ $$ p ↔q = (p∧q) ∨ (-p∧-q) $$ There may be other properties also that I...- Raghav Gupta
- Thread
- Algebra Boolean algebra Rules Transformation
- Replies: 8
- Forum: Set Theory, Logic, Probability, Statistics
-
J
Undergrad The "x'=x-vt" in Galilean/Lorentz transformation
Hello people, I have a question regarding the x' component in the Lorentz/Galilean transformation. So from what i understand is that there are 2 coordinate systems used in the transformations. One is used as a reference point and one is used for moving away from this point. The moving away in...- JohnTitor
- Thread
- Galilean transformation Lorentz transformation Transformation
- Replies: 3
- Forum: Special and General Relativity
-
C
MHB Definition of matrix transformation
Hi all, I have the definition of a linear transformation in terms of a transformation matrix. So the mapping is a function $f:\mathbb{R}^m\rightarrow\mathbb{R}^n$, where $f(\textbf{x})=A\textbf{x}$ and $A$ is a $n\times m$ matrix. I'm looking for a similar definition for a transformation that...- Carla1985
- Thread
- Definition Matrix Transformation
- Replies: 3
- Forum: Linear and Abstract Algebra
-

Finding properties of a linear transformation
Homework Statement Find the domain, target space, image, rank and nullity of the linear transformation T(A)=Av, where v= (1, 2) and A is any 2×2matrix. Homework Equations The Attempt at a Solution I believe I know the domain (R2x2 vector space) and target space (R2), but I am not sure how to...- papaross
- Thread
- Homework Linear Linear algebra Linear transformation Properties Transformation
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
K
MHB Mobius transformation satisfying certain properties
I'm having some trouble showing that a Mobius transformation $F$ maps $0$ to $\infty$ and $\infty$ to $0$ iff $F(z)=dz^{-1}$ for some $d \in \mathbb{C}.$ Mainly with the "only if" part. Do I need to use pictures? This is Exercise $23$ in Section $3.3$ of Conway's *Functions of One Complex...- kalish1
- Thread
- Properties Transformation
- Replies: 1
- Forum: Topology and Analysis
-

Graduate Schwarzschild Extension Coordinate Transformation Algebra
So I have the metric as ##ds^{2}=-(1-\frac{2m}{r})dt^{2}+(1-\frac{2m}{r})^{-1}dr^{2}+r^{2}d\Omega^{2}##* I have transformed to coordinate system ##u,r,\phi, \theta ##, where ##u=t-r*##(2), where ##r*=r+2m In(\frac{r}{2m}-1)## and to the coordinate system ##v,r,\phi, \theta ##, where...- binbagsss
- Thread
- Algebra Coordinate Coordinate transformation Extension Schwarzschild Transformation
- Replies: 8
- Forum: Special and General Relativity
-
Graduate How Does the Element of Solid Angle Transform Under Lorentz Transformation?
I'm trying to figure out how the element of solid angle transforms under a transformation between two inertial frames moving with velocity v w.r.t. each other under an arbitrary direction. But I should say I disappointed myself! Anyway, some books which contain a brief discussion on this(which...- ShayanJ
- Thread
- Angle Solid Solid angle Transformation
- Replies: 12
- Forum: Special and General Relativity
-
G
Linear transformation D:P2 --> P2
Linear transformation D:Psub2 to Psub2 defined by D( Asub0 + Asub1x + Asub2x^2) = Asub1 + 2Asub2x Find the matrix of this linear transformation with respect to the ordered bases C to C, where C= { 1-x , 1+ x, x^2 } I know that D stands for differentiating . D prime is Asub1 + 2Asub2x I...- gildee
- Thread
- Linear Linear transformation Transformation
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

Find a linear transformation such that it maps the disk onto
Homework Statement Find a linear transformation w = f(z) such that it maps the disk Δ(2) onto the right half-plane {w | Re(w) > 0} satisfying f(0) = 1 and arg f'(0) = π/2 Homework Equations w = f(z) = \frac{az+b}{cz+d} z = f^{-1}(w) = \frac{dw-b}{-cw+a} The Attempt at a Solution [/B]...- Shackleford
- Thread
- Disk Linear Linear transformation Transformation
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
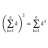
Graduate Hilbert space transformation under Poincaré translation
This is one of those "existential doubts" that most likely have a trivial solution which I can't see. Veltman says in the Diagrammatica book: Although the reasoning makes perfect sense for a Hilbert space spanned by momentum states, intuitively it doesn't make sense to me, because a...- ddd123
- Thread
- Hilbert Hilbert space Poincare Space Transformation Translation
- Replies: 3
- Forum: Quantum Physics
-

Proving a transformation is linear
Homework Statement If T is linear, show that it is linear by finding a standard matrix A for T so that: Also show that this equation holds for the matrix you have found. If T is not linear, prove that T is not linear by showing that it does not fit the definition of a linear transformation...- _N3WTON_
- Thread
- Linear Transformation
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Transformation of electronic audio signal into audible Sound
Hello Guyz I've got a little Question For Seniors I hope You answer it Briefly , I know that whenever i plug in my USB Drive in my Loudspeaker or plug Speaker itself in my PC and play anything like a song an Electrical audio Signal is Produced which is transformed by Speaker into a audible...- AustinTahir
- Thread
- Audio Electronic Signal Sound Transformation
- Replies: 3
- Forum: Electrical Engineering
-
R
Component functions and coordinates of linear transformation
Let A(a, b, c) and A'(a′,b′,c′) be two distinct points in R3. Let f from [0 , 1] to R3 be defined by f(t) = (1 -t) A + t A'. Instead of calling the component functions of f ,(f1, f2, f3) let us simply write f = (x, y, z). Express x; y; z in terms of the coordinates of A and A, and t. I thought...- raghad
- Thread
- Component Coordinates Derivatives Functions Linear Linear transformation Multivariable calculus Real analysis Transformation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
W
Graduate Twice of supersymmetric transformation = translation
Hello, I have one conceptual question. I have been working on Supersymmetry. Now, I understand that twice of supersymmetric transformation is equivalent to translation mathematically(naively). However, I don't quite understand why this should be the case conceptually. Supersymmetric...- wphysics
- Thread
- Supersymmetry Transformation Translation
- Replies: 12
- Forum: Beyond the Standard Models
-
P
Graduate Find lorentz transformation for arbitrary velocity (v) relat
Hello i have to find the Lorentz transformation for arbitrary velocity (v) relative to (O) the information's i have: 1-i have to use all 3 components of velocity ##(V_x, V_y, V_z )## 2- ##x'=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}## ##y'=y## ##z'=z## 3-...- Pual Black
- Thread
- Lorentz Lorentz transformation Transformation Velocity
- Replies: 19
- Forum: Special and General Relativity
-
Graduate How to Transform Integrals from Cylindrical to Spherical Coordinates?
Consider an integral of the type ## \int_0^{a} \int_0^{\pi} g(\rho,\varphi,\theta) \rho d\varphi d\rho ##. As you can see, the integral is w.r.t. cylindrical coordinates on a plane but the integrand is also a function of ##\theta## which is a spherical coordinate. So for evaluating it, there are... -
R
Quantum Mechanics: Transformation Matrix
Homework Statement Determine a ##2\times 2## matrix ##\mathbb{S}## that can be used to transform a column vector representing a photon polarization state using the linear polarization vectors ##|x\rangle## and ##|y\rangle## as a basis to one using the circular polarization vectors...- Robben
- Thread
- Matrix Mechanics Quantum Quantum mechanics Transformation Transformation matrix
- Replies: 3
- Forum: Advanced Physics Homework Help
-
B
MHB Range and Image of a Transformation
$\textbf{Problem}$ Let $\textbf{b} = \begin{bmatrix}\begin{array}{r} 8 \\ 7 \\ 5 \\ -3 \end{array}\end{bmatrix}$ and let $A = \begin{bmatrix} 2 & 3 & 5 & - 5 \\ -7 & 7 & 0 & 0 \\ -3 & 4 & 1 & 3 \\ -9 & 3 & -6 & -4 \end{bmatrix}$ Is $\textbf{b}$ in the range of the transformation $\textbf{x}...- bwpbruce
- Thread
- Image Range Transformation
- Replies: 6
- Forum: Linear and Abstract Algebra
-
Y
Graduate Nonlinear transform can separate function composition?
I am solving a nonlinear ODE in the form of Newton's Second Law. In the equation, there is a Heaviside Theta Function of the function which I am solving (##\theta (x(t)##). Since it is quite troublesome to have both the left side of the ODE and the imput of the ODE to contain function of unknown...- Yunjia
- Thread
- Chaos Composition Function Nonlinear Transform Transformation
- Replies: 1
- Forum: Differential Equations
-
B
MHB Violation of Linear Transformation?
This is a solution that I observed from my textbook to a linear transformation problem: Isn't $T$ not linear since $\textbf{x} \ne \textbf{0}$? Property iii of the Definition of Linear Transformation states $T(\textbf{(0)} = \textbf{0}$ so something is contradictory here.- bwpbruce
- Thread
- Linear Linear transformation Transformation
- Replies: 6
- Forum: Linear and Abstract Algebra
-
B
MHB Sketch of the Reflection Transformation of a Parallelogram
$\textbf{Problem:}$ Let $T: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ be the linear transformation that reflects each point through the $x_2$ axis. Make two sketches that illustrate properties of linear transformation. $\textbf{Solution:}$ Let $T(\textbf{x}) = \begin{bmatrix} -1 & 0 \\ 0 & 1...- bwpbruce
- Thread
- Parallelogram Reflection Sketch Transformation
- Replies: 2
- Forum: Linear and Abstract Algebra
-
B
MHB Transformation of a Parallelogram
$\textbf{Problem}$ Let $\textbf{u}$ and $\textbf{v}$ be vectors in $\mathbb{R}^n$. It can be shown that the set $P$ of all points in the parallelogram determined by $\textbf{u}$ and $\textbf{v}$ has the form $a\textbf{u} + b\textbf{v}$, for $0 \le a \le 1, 0 \le b \le 1$. Let $T: \mathbb{R}^n...- bwpbruce
- Thread
- Parallelogram Transformation
- Replies: 3
- Forum: Linear and Abstract Algebra
-
B
MHB Linear Transformation of a Plane
$\textbf{Problem}$ Let $\textbf{u}$ and $\textbf{v}$ be linearly independent vectors in $\mathbb{R}^3$, and let $P$ be the plane through $\textbf{u}, \textbf{v}$ and $\textbf{0}.$ The parametric equation of $P$ is $\textbf{x} = s\textbf{u} + \textbf{v}$ (with $s$, $t$ in $\mathbb{R}$). Show that...- bwpbruce
- Thread
- Linear Linear transformation Plane Transformation
- Replies: 2
- Forum: Linear and Abstract Algebra
-

Undergrad Prove to myself that rotation is a linear transformation?
How do you prove that rotation of a vector is a linear transformation? It's intuitive (although not completely crystal clear to me) that it is a linear transformation at the 2d level, but how do I prove it to myself (that this is a general property of rotations)? For example, rotate vector...- davidbenari
- Thread
- Linear Linear transformation Rotation Transformation
- Replies: 4
- Forum: Linear and Abstract Algebra
-
B
MHB Transformation of a Line Segment
$\textbf{Problem}$ The line segment from $\textbf{p}$ to $\textbf{q}$ is the set of points of the form $(1 - t)\textbf{p} + t\textbf{q}$ for $0 \le t \le 1$ (as shown in the figure below). Show that a linear transformation, $T$, maps this line segment onto a line segment or onto a single point...- bwpbruce
- Thread
- Line Transformation
- Replies: 6
- Forum: Linear and Abstract Algebra
-
B
MHB Show that a Parametric Equation Maps To Another Line By Linear Transformation.
$\textbf{Problem}$ Given $\textbf{v} \ne \textbf{0}$ and $\textbf{p}$ in $\mathbb{R}^n$, the line through $\textbf{p}$ in the direction of $\textbf{v}$ is given by $\textbf{x} = \textbf{p} + t\textbf{v}$. Show that linear transformation $T: \mathbb{R}^n \rightarrow \mathbb{R}^n$ maps this line...- bwpbruce
- Thread
- Line Linear Linear transformation Parametric Transformation
- Replies: 3
- Forum: Linear and Abstract Algebra
-
B
MHB Is $f(x) = mx + b$ a Linear Transformation?
Define $f: \mathbb{R} \rightarrow \mathbb{R}$ by $f(x) = mx + b$. $\textbf{a.}$ Show that $f$ is a linear transformation when $b = 0$. $\textbf{b.}$ Find a property of linear transformation that is violated when $b = 0$ $\textbf{c.}$ Why is $f$ called a linear function?- bwpbruce
- Thread
- Function Linear Linear transformation Transformation
- Replies: 11
- Forum: Linear and Abstract Algebra