Examples of Prequantum Field Theories II: Higher Gauge Fields

 

 

 

After having recalled ordinary gauge fields from a dg-algebraic perspective in the previous article, here I discuss how in these terms we easily get the concept of higher (nonabelian) gauge fields, i.e. of gauge fields whose “vector potential” is not just a 1-form but involves differential forms of higher degree. These will be the fields of the prequantum Chern-Simons type fields theories to be discussed in the next article.

---

 

 

Ordinary gauge fields are characterized by the property that there are no non-trivial gauge-of-gauge transformations, equivalently that their BRST complexes contain no higher-order ghosts. Mathematically, it is natural to generalize beyond this case to higher gauge fields, which do have non-trivial higher gauge transformations.

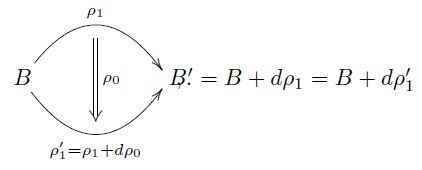
The simplest example is a “2-form field” (B-field), generalizing the “vector potential” 1-form $A$ of the electromagnetic field. Where such a 1-form has gauge transformations given by 0-forms (functions) $\kappa$ via $$A \stackrel{\kappa}{\longrightarrow} A’ = A +d\kappa\,,$$ a 2-form $B$ has gauge transformations given by 1-forms $\rho_1$, which themselves then have gauge-of-gauge-transformations given by 0-forms $\rho_0$:

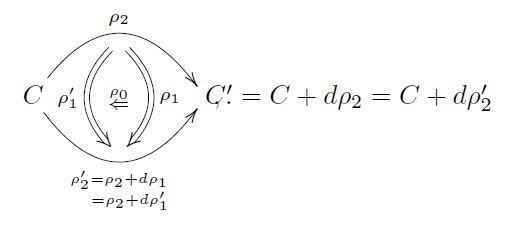
Next a “3-form field” (C-field’) has third order gauge transformations:

Similarly “$n$-form fields” have order-$n$ gauge-of-gauge transformations and hence have order-$n$ ghost-of-ghosts in their BRST complexes.

Higher gauge fields have not been experimentally observed, to date, as fundamental fields of nature, but they appear by necessity and ubiquitously in higher-dimensional supergravity and in the hypothetical physics of strings and $p$-branes. The higher differential geometry which we develop is to a large extent motivated by making precise and tractable the global structure of higher gauge fields in string and M-theory.

Generally, higher gauge fields are part of mathematical physics just as the Ising model and $\phi^4$-theory are, and as such, they do serve to illuminate the structure of experimentally verified physics.

For instance, the Einstein equations of motion for ordinary (bosonic) general relativity on 11-dimensional spacetimes are equivalent to the full super-torsion constraint in 11-dimensional supergravity with its 3-form higher gauge field [CandielloLechner 93].  From this point of view, one may regard the 3-form higher gauge field in supergravity, together with the gravitino, as auxiliary fields that serve to present Einstein’s equations for the graviton in a particularly neat mathematical way.

We now use the above dg-algebraic formulation of ordinary gauge fields from the previous article in order to give a quick but accurate idea of the mathematical structure of higher gauge fields.

---

 

Above we saw that (finite-dimensional) Lie algebras are equivalently the formal duals of those differential graded-commutative algebras whose underlying graded commutative algebra is freely generated from a (finite-dimensional) vector space over the ground field. From this perspective, there are two evident generalizations to be considered: we may take the underlying vector space to already have contributions in higher degrees itself, and we may pass from vector spaces, being modules over the ground field $\mathbb{R}$, to (finite rank) projective modules over an algebra of smooth functions on a smooth manifold.

Hence we say that an $L_\infty$-algebroid (of finite type) is a smooth manifold $X$ equipped with a $\mathbb{N}$-graded vector bundle (degreewise of finite rank), whose smooth sections hence form an $\mathbb{N}$-graded projective $C^\infty(X)$-module $\mathfrak{a}_\bullet$, and equipped with an $\mathbb{R}$-linear differential $d_{\mathrm{CE}}$ on the Grassmann algebra of the $C^\infty(X)$-dual $\mathfrak{a}^\ast$ modules
$$
\mathrm{CE}(\mathfrak{a})
:=
\left(
\wedge^\bullet_{C^\infty(X)}(\mathfrak{a}^\ast),
\;
d_{\mathrm{CE}(\mathfrak{a})}
\right)
\,.
$$
Accordingly, a homomorphism of $L_\infty$-algebroids we take to be a dg-algebra homomorphism (over $\mathbb{R}$) of their CE-algebras going the other way around. Hence the category of $L_\infty$-algebroids is the full subcategory of the opposite of that of differential graded-commutative algebras over $\mathbb{R}$ on those whose underlying graded-commutative algebra is free on graded locally free projective $C^\infty(X)$-modules:
$$
L_\infty\mathrm{Algbd}
\hookrightarrow
\mathrm{dgcAlg}^\mathrm{op}
\,.
$$
We say we have a Lie n-algebroid when $\mathfrak{a}_\bullet$ is concentrated in the lowest $n$-degrees. Here are some important examples of $L_\infty$-algebroids:

When the base space is the point, $X = \ast$, and $\mathfrak{a}$ is concentrated in degree 0, then
we recover Lie algebras. Generally, when the base space is the point, then the $\mathbb{N}$-graded module $\mathfrak{a}$
is just an $\mathbb{N}$-graded vector space $\mathfrak{g}$. We write $\mathfrak{a} = \mathbf{B}\mathfrak{g}$ to indicate this, and then $\mathfrak{g}$ is an L-infinity algebra. When in addition $\mathfrak{g}$ is concentrated in the lowest $n$ degrees, then these are also called Lie n-algebras. With no constraint on the grading but assuming that the differential sends single generators always to sums of wedge products of at most two generators, then we get dg-Lie algebras.

The Weil algebra of a Lie algebra $\mathfrak{g}$ hence exhibits a Lie 2-algebra. We may think of this as the Lie 2-algebra
$\mathrm{inn}(\mathfrak{g})$ of inner derivations of $\mathfrak{g}$. By the above discussion, it is suggestive to write $\mathbf{E}\mathfrak{g}$ for this Lie 2-algebra, hence
$$
\mathrm{W}(\mathbf{B}\mathfrak{g}) = \mathrm{CE}(\mathbf{B}\mathbf{E}\mathfrak{g})
\,.
$$

If $\mathfrak{g} = \mathbb{R}[n]$ is concentrated in degree $p$ on the real line (so that the CE-differential is necessarily trivial), then we speak of the line Lie (p+1)-algebra $\mathbf{B}^p \mathbb{R}$, which as an $L_\infty$-algebroid over the point is to be denoted
$$
\mathbf{B}\mathbf{B}^{p}\mathbb{R} = \mathbf{B}^{p+1}\mathbb{R}
\,.
$$

All this goes through verbatim, up to additional signs, with all vector spaces generalized to super-vector spaces. The Chevalley-Eilenberg algebras of the resulting super L-infinity algebras are known in parts of the supergravity literature
“FDA“s. This had been the topic of the previous articles Homotopy Lie n-algebras in supergravity and Emergence from the superpoint.

Passing now to $L_\infty$-algebroids over non-trivial base spaces, first of all, every smooth manifold $X$ may be regarded as the $L_\infty$-algebroid over $X$, these are the Lie 0-algebroids. We just write $\mathfrak{a} = X$ when the context is clear.

For the tangent bundle $T X$ over $X$ then the graded algebra of its dual sections is the wedge product algebra of differential forms,
$\mathrm{CE}(T X ) = \Omega^\bullet(X)$ and hence the de Rham differential makes $\wedge^\bullet \Gamma(T^\ast X)$ into a dgc-algebra and hence makes $T X$ into a Lie algebroid. This is called the tangent Lie algebroid of $X$. We usually write $\mathfrak{a} = TX$ for the tangent Lie algebroid (trusting that context makes it clear that we do not mean the Lie 0-algebroid over the underlying manifold of the tangent bundle itself). In particular this means that for any other $L_\infty$-algebroid $\mathfrak{a}$ then flat $\mathfrak{a}$-valued differential forms on some smooth manifold $\Sigma$ are equivalently homomorphisms of $L_\infty$-algebroids like so:
$$
\Omega_{\mathrm{flat}}(\Sigma,\mathfrak{a})
\;\;=\;\;
\left\{
\; T \Sigma \longrightarrow \mathfrak{a}\;
\right\}
\,.
$$
In particular ordinary closed differential forms of degree $n$ are equivalently flat $\mathbf{B}^n\mathbb{R}$-valued differential forms:
$$
\Omega^n_{\mathrm{cl}}(\Sigma)
\;\; \simeq \;\;
\left\{
\; T \Sigma \longrightarrow \mathbf{B}^n \mathbb{R}\;
\right\}
\,.
$$

More generally, for $\mathfrak{a}$ any $L_\infty$-algebroid over some base manifold $X$, then we have its Weil dgc-algebra
$$
\mathrm{W}(\mathfrak{a})
:=
\left(
\wedge^\bullet_{C^\infty(X)}( \mathfrak{a}^\ast \oplus \Gamma(T^\ast X) \oplus \mathfrak{a}^\ast[1] ),
d_{\mathrm{W}} = d_{\mathrm{CE}} + \mathbf{d} )
\right)
\,,
$$
where $\mathbf{d}$ acts as the degree shift isomorphism in the components $\wedge^1_{C^\infty(X)}\mathfrak{a}^\ast \longrightarrow \wedge^1_{C^\infty(X)}\mathfrak{a}^\ast[1]$ and as the de Rham differential in the components $\wedge^k \Gamma(T^\ast X) \to \wedge^{k+1}\Gamma(T^\ast X)$. This defines a new $L_\infty$-algebroid that may be called the tangent $L_\infty$-algebroid $T \mathfrak{a}$
$$
\mathrm{CE}(T \mathfrak{a}) := \mathrm{W}(\mathfrak{a})
\,.
$$
We also write $\mathbf{E}\mathbf{B}^p \mathbb{R}$ for the $L_\infty$-algebroid with
$$
\mathrm{CE}(\mathbf{E}\mathbf{B}^p \mathbb{R})
:=
\mathrm{W}(\mathbf{B}^{p}\mathbb{R})
\,.
$$

In direct analogy with the discussion for Lie algebras, we then say that an unconstrained $\mathfrak{a}$-valued differential form $A$ on a manifold $\Sigma$ is a dg-algebra homomorphism from the Weil algebra of $\mathfrak{a}$ to the de Rham dg-algebra on $\Sigma$:
$$
\Omega(\Sigma,\mathfrak{a})
:=
\left\{
\; \Omega^\bullet(\Sigma) \longleftarrow \mathrm{W}(\mathfrak{a}) \;
\right\}
\,.
$$

For $G$ a Lie group acting on $X$ by diffeomorphisms, then there is the action Lie algebroid $X/\mathfrak{g}$ over $X$ with $\mathfrak{a}_0 = \Gamma_X(X \times \mathfrak{g})$ the $\mathfrak{g}$-valued smooth functions over $X$. Write $\rho : \mathfrak{g} \to \mathrm{Vect}$ for the linearized action. With a choice of basis $\{t_a\}$ for $\mathfrak{g}$ as before
and assuming that $X = \mathbb{R}^n$ with canonical coordinates $x^i$, then $\rho$ has components $\{\rho_a^\mu\}$ and the CE-differential on $\wedge^\bullet_{C^\infty(X)} (\Gamma_X(X \times \mathfrak{g}^\ast))$ is given on generators by
$$
\begin{aligned}
d_{\mathrm{CE}} &: f \mapsto t^a \rho_a^\mu \partial_\mu f
\\
d_{\mathrm{CE}} &: t^a \mapsto \tfrac{1}{2}C^{a}{}_{b c} t^b \wedge t^c
\end{aligned}
\,.
$$
In the physics literature this Chevalley-Eilenberg algebra $\mathrm{CE}(X/\mathfrak{g})$ is known as the BRST complex of $X$ for infinitesimal symmetries $\mathfrak{g}$. If $X$ is thought of as a space of fields, then the $t_a$ are called ghost fields.

Given any $L_\infty$-algebroid, it induces a whole bouquet of further $L_\infty$-algebroids via extension by higher cocycles.
A $p+1$-cocycle on an $L_\infty$-algebroid $\mathfrak{a}$ is a closed element
$$
\mu \in (\wedge^\bullet_{C^\infty(X)}\mathfrak{a}^\ast)_{p+1} \hookrightarrow \mathrm{CE}(\mathfrak{a})
\,.
$$
Notice that now cocycles are representable by the higher line $L_\infty$-algebras $\mathbf{B}^{p+1}\mathbb{R}$ from above:
$$
\begin{aligned}
\left\{
\mu \in \mathrm{CE}(\mathfrak{a})_{p+1} \;|\; d_{\mathrm{CE}}\mu = 0
\right\}
&
\simeq
\left\{
\;
\mathrm{CE}(\mathfrak{a})
\stackrel{\mu^\ast}{\longleftarrow}
\mathrm{CE}(\mathbf{B}^{p+1}\mathbb{R})
\;
\right\}
\\
& =
\left\{
\;
\mathfrak{a} \stackrel{\mu}{\longrightarrow} \mathbf{B}^{p+1}\mathbb{R}
\;
\right\}
\end{aligned}
\,.
$$

It is a traditional fact that $\mathbb{R}$-valued 2-cocycles on a Lie algebra induce central Lie algebra extensions. More generally,
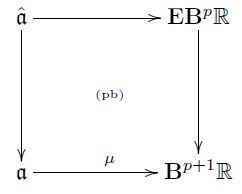
higher cocycles $\mu$ on an $L_\infty$-algebroid induce $L_\infty$-extensions $\hat {\mathfrak{a}}$, given by the pullback

Equivalently this makes $\hat{\mathfrak{a}}$ be the homotopy fiber of $\mu$ in the homotopy theory of $L_\infty$-algebras, and induces a long homotopy fiber sequence of the form

In components this means simply that $\mathrm{CE}(\hat{\mathfrak{a}})$ is obtained from $\mathrm{CE}(\mathfrak{a})$ by adding one generator $c$ in degre $p$ and extending the differential to it by the formula
$$
d_{\mathrm{CE}} : c = \mu
\,.
$$
This construction has a long tradition in the supergravity literature, we discussed this before in Emergence form the superpoint.

For example for $\mathfrak{g}$ a semisimple Lie algebra with binary invariant polynomial $\langle -,-\rangle$ (the Killing form), then $\mu_3 = \langle-,[-,-]\rangle$ is a 3-cocycle. The $L_\infty$-extension by this cocycle is a Lie 2-algebra called the string Lie 2-algebra $\mathfrak{string}_\mathfrak{g}$. If $\{t^a\}$ is a linear basis of $\mathfrak{g}^\ast$ as before write $k_{a b} := \langle t_a, t_b\rangle$ for the components of the Killing form; the components of the 3-cocycle are $\mu_{a b c} = k_{a a’}C^{a’}{}_{b c}$. The CE-algebra of the string Lie 2-algebra then is that of $\mathfrak{g}$ with a generator $b$ added and with CE differential defined by
$$
\begin{aligned}
d_{\mathrm{CE}(\mathfrak{string})} & : t^a \mapsto \tfrac{1}{2}C^a{}_{b c} t^b \wedge t^c
\\
d_{\mathrm{CE}(\mathfrak{string})} & : b \mapsto k_{a a’}C^{a’}{}_{c b} t^a \wedge t^b \wedge t^c
\,.
\end{aligned}
$$
Hence a flat $\mathfrak{string}_{\mathfrak{g}}$-valued differential form on some $\Sigma$ is a pair consisting of an ordinary flat $\mathfrak{g}$-valued 1-form $A$ and of a 2-form $B$ whose differential has to equal the evaluation of $A$ in the 3-cocoycle:
$$
\Omega_{\mathrm{flat}}(\Sigma,\mathfrak{string}_{\mathfrak{g}})
\;\simeq\;
\left\{
(A,B) \in \Omega^1(\Sigma,\mathfrak{g})\times\Omega^2(\Sigma)
\;|\;
F_A = 0 \,,\;\; d B = \langle A \wedge [A \wedge A]\rangle
\right\}
\,.
$$
Notice that since $A$ is flat, the 3-form $\langle A \wedge [A \wedge A]\rangle$ is its Chern-Simons 3-form. More generally, Chern-Simons forms are such that their differential is the evaluation of the curvature of $A$ in an invariant polynomial.

---

 

An invariant polynomial $\langle -\rangle$ on an $L_\infty$-algebroid we may take to be a $d_{\mathrm{W}}$-closed element in the shifted generators of its Weil algebra $\mathrm{W}(\mathfrak{a})$
$$
\langle -\rangle \in \wedge^\bullet_{C^\infty(X)}(\mathfrak{a}^\ast[1]) \hookrightarrow \mathrm{W}(\mathfrak{a})
\,.
$$
When one requires the invariant polynomial to be binary, i.e. in $\wedge^2 (\mathfrak{a}^\ast[1]) \to \mathrm{W}(\mathfrak{a})$ and non-degenerate, then it is also called a shifted symplectic form and it makes $\mathfrak{a}$ into a symplectic Lie n-algebroid. For $n = 0$ these are the symplectic manifolds, for $n = 1$ these are called Poisson Lie algebroids, for $n = 2$ they are called Courant Lie 2-algebroids \cite{RoytenbergCourant}. There are also plenty of non-binary invariant polynomials.

Being $d_{\mathrm{W}}$-closed, an invariant polynomial on $\mathfrak{a}$ is represented by a dg-homomorphism:
$$
W(\mathfrak{a}) \longleftarrow \mathrm{CE}(\mathbf{B}^{p+2}\mathbb{R}) : \langle – \rangle
$$
This means that given an invariant polynomial $\langle -\rangle$ for an $L_\infty$-algebroid $\mathfrak{a}$, then it assigns to any $\mathfrak{a}$-valued differential form $A$ a plain closed $(p+2)$-form $\langle F_A\rangle$ made up of the $\mathfrak{a}$-curvature forms, namely the composite
$$
\Omega^\bullet(\Sigma)
\stackrel{A}{\longleftarrow}
W(\mathfrak{a})
\stackrel{\langle -\rangle}{\longleftarrow} \mathrm{CE}(\mathbf{B}^{p+2}\mathbb{R}) : \langle F_A \rangle
\,.
$$
In other words, $A$ may be regarded as a nonabelian pre-quantization of $\langle F_A\rangle$.

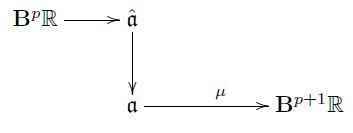
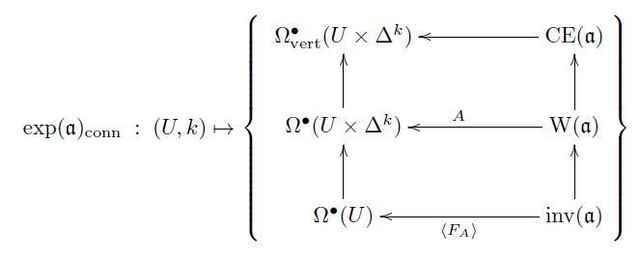
Therefore we may consider now the $\infty$-groupoid of $\mathfrak{a}$-connections whose gauge transformations preserve the specified invariant polynomial, such as to guarantee that it remains a globally well-defined differential form. The smooth $\infty$-groupoid of $\mathfrak{a}$-valued connections with such gauge transformations between them we write $\exp(\mathfrak{a})_{\mathrm{conn}}$. As a smooth simplicial presheaf, it is hence given by the following assignment:

Here on the right we have, for every $U$ and $k$,  the set of those $A$ on $U \times \Delta^k$ that induce gauge transformations along the $\Delta^k$-direction (that is the commutativity of the top square) such that the given invariant polynomials evaluated on the curvatures are preserved (that is the commutativity of the bottom square).

This $\exp(\mathfrak{a})_{\mathrm{conn}}$ is the moduli stack of $\mathfrak{a}$-valued connections with gauge transformations
and gauge-of-gauge transformations between them that preserve the chosen invariant polynomials.

The key example is the moduli stack of $(p+1)$-form gauge fields
$$
\exp(\mathbf{B}^{p+1}\mathbb{R})_{\mathrm{conn}}/\mathbb{Z}
\simeq
\mathbf{B}(\mathbb{R}/_{\!\hbar}\mathbb{Z})_{\mathrm{conn}}
$$

Generically we write
$$
\mathbf{A}_{\mathrm{conn}} := \mathrm{cosk}_{n+1} (\exp(\mathfrak{a})_{\mathrm{conn}})
$$
for the $n$-truncation of a higher smooth stack of $\mathfrak{a}$-valued gauge field connections obtained this way. If $\mathfrak{a} = \mathbf{B}\mathfrak{g}$ then we write $\mathbf{B}G_{\mathrm{conn}}$ for this.

Given such, then an $\mathfrak{a}$-gauge field on $\Sigma$ (an $\mathbf{A}$-principal connection) is equivalently a map of smooth higher stacks
$$
\nabla : \Sigma \longrightarrow \mathbf{A}_{\mathrm{conn}}
\,.
$$
By the above discussion, a simple map like this subsumes all of the following component data:

• a choice of open cover $\{U_i \to \Sigma\}$;
• a $\mathfrak{a}$-valued differential form $A_i$ on each chart $U_i$;
• on each intersection $U_{i j}$ of charts a path of infinitesimal gauge symmetries whose integrated finite gauge symmetry $g_{i j}$ takes $A_i$ to $A_j$;
• on each triple intersection $U_{i j k}$ of charts a path-of-paths of infinitesimal gauge symmetries whose integrated finite gauge-of-gauge symmetry takes the gauge transformation $g_{i j}\cdot g_{j k}$ to the gauge transformation $g_{i k}$
• and so on.

Hence a $\mathfrak{a}$-gauge field is locally $\mathfrak{a}$-valued differential form data which are coherently glued together to a global structure by gauge transformations and higher-order gauge-of-gauge transformations.

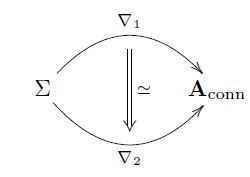
Given two globally defined $\mathfrak{a}$-valued gauge fields this way, then a globally defined gauge transformation them is equivalently a homotopy between maps of smooth higher stacks

Again, this concisely encodes a system of local data: this is on each chart $U_i$ a path of infinitesimal gauge symmetries whose integrated gauge transformation transforms the local $\mathfrak{a}$-valued forms into each other, together with various higher-order gauge transformations and compatibilities on higher-order intersections of charts.

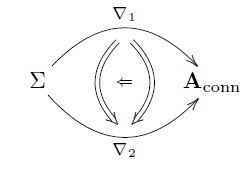
Then a gauge-of-gauge transformation is a homotopy of homotopies

and again this encodes a recipe for how to extract the corresponding local differential form data.

 

For more on all these constructions, see [Sati-Schreiber-Stasheff 09] [Fiorenza-Schreiber-Stasheff 10] [Fiorenza-Rogers-Schreiber 11].

---

 

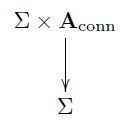
In conclusion, the correct higher field bundle for $\mathfrak{a}$-gauge theory is the stacky bundle of the form

(see also the exposition at Higher field bundles for gauge fields). The next article discusses how from transgressive cocycles on $L_\infty$-algebroids one may construct prequantum field theory Lagrangians on such field bundles.

Click For Forum Comments