Higher Prequantum Geometry III: The Global Action Functional – Cohomologically
Show Complete Series
Part 1: Higher Prequantum Geometry I: The Need for Prequantum Geometry
Part 2: Higher Prequantum Geometry II: The Principle of Extremal Action – Comonadically
Part 3: Higher Prequantum Geometry III: The Global Action Functional — Cohomologically
Part 4: Higher Prequantum Geometry IV: The Covariant Phase Space – Transgressively
Part 5: Higher Prequantum Geometry V: The Local Observables – Lie Theoretically
Part 6: Examples of Prequantum Field Theories I: Gauge Fields
Part 7: Examples of Prequantum Field Theories II: Higher Gauge Fields
Part 8: Examples of Prequantum Field Theories III: Chern-Simons-type Theories
Part 9: Examples of Prequantum Field Theories IV: Wess-Zumino-Witten-type Theories
Part 10: Introduction to Perturbative Quantum Field Theory
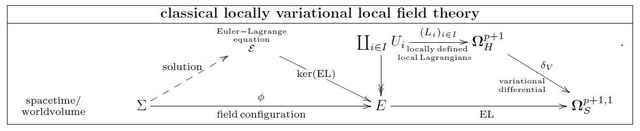
The previous article ended with the concept of classical locally variational field theories, of which a class of examples are field theories of higher WZW type. To recall, in the diagrammatics that we established, such theories were concisely expressed like so:
Here we discuss how asking such theories to have a well-defined global action functional necessarily leads to their pre-quantization by promoting the system of locally defined Lagrangian forms ##L_i## to a globally coherent structure. In the next article, this allows us to pick some fruit: we will see how that global coherence structure automatically pre-quantizes the covariant phase space of any locally variational field theory.
This article is indebted to discussion with Igor Khavkine.
For a globally defined Lagrangian ##(p+1)##-form ##L_{p+1}## on the jet bundle of the given field bundle, then the value of the action functional on a compactly supported field configuration ##\phi## is simply the integral
$$
S(\phi) := \int_\Sigma j^\infty(\phi)^\ast L_{p+1}
$$
of the Lagrangian, evaluated on the field configuration, over spacetime/worldvolume.
But when Lagrangian forms are only defined patchwise on a cover ##\{U_i \to E\}_i## as in the above diagram, then there is no way to globally make invariant sense of the action functional! As soon as sections pass through several patches, then making invariant sense of such an integral requires more data, in particular, it requires more than just a compatibility condition of the locally defined Lagrangian forms on double intersections.
The problem of what exactly it takes to define global integrals of locally defined forms has long found a precise answer in mathematics, in the theory of ordinary differential cohomology. This has several equivalent incarnations, the one closest to classical constructions in differential geometry involves Cech cocycles:
one first needs to choose on each intersection ##U_{i j}## of two patches ##U_i## and ##U_j## a differential form ##(\kappa_{p})_{i j}## of degree ##p##, whose horizontal de Rham differential is the difference between the two Lagrangians restricted to that intersection
$$
(L_{p+1})_j – (L_{p+1})_i = d_H (\kappa_p)_{i j}
\,.
$$
Then further one needs to choose on each triple intersection ##U_{i j k}## a horizontal differential form ##(\kappa_{p-1})_{i j k}## of degree ##p-1## whose horizontal differential is the alternating sum of the relevant three previously defined forms:
$$
(\kappa_p)_{j k} – (\kappa_p)_{i k} + (\kappa_p)_{i j} = d_H (\kappa_{p-1})_{i j k }
\,.
$$
And so on. Finally on ##(p+2)##-fold intersections one needs to choose smooth functions ##(\kappa_0)_{i_0 \cdots i_{p+1}}## whose horizontal differential is the alternating sum of ##(p+2)## of the previously chosen horizontal 1-forms, and, moreover, on ##(p+3)##-fold intersections the alternating sum of these functions has to vanish.
Such a tuple ##(\{U_i\}; \{(L_{p+1})_i\},\, \{(\kappa_{p})_{i j}\}, \cdots)## is a horizontal Cech-de Rham cocycle in degree ##(p+2)##.
Given such, there is then a way to make sense of global integrals: one chooses a triangulation subordinate to the given cover, then integrates the locally defined Lagrangians ##(L_{p+1})_i## over the ##(p+1)##-dimensional cells of the triangulation, integrates the gluing forms ##(\kappa_p)_{i j}## over the ##p##-dimensional faces of these cells, the higher gluing forms ##(\kappa_p)_{i j k}## over the faces of these faces, etc., and sums all this up. This defines a global action functional, which we may denote by
$$
S(\phi) := \int_{\Sigma} j^\infty(\phi)^\ast(\{{L}_i\},\, \{(\kappa_p)_{i j}\}, \cdots)
\,.
$$
This horizontal Cech-de Rham cocycle data is subject to fairly evident coboundary relations (gauge transformations)
that themselves are parameterized by systems ##(\rho_\bullet)## of ##(p+1)-k##-forms on ##k##-fold intersections:
$$
\begin{aligned}
L_i & \mapsto L_i + d_H (\rho_{p})_i
\\
(\kappa_{p})_{i j} & \mapsto (\kappa_p)_{i j} + d_H (\rho_{p-1})_{i j} + (\rho_p)_j – (\rho_p)_i
\\
\vdots
\end{aligned}
$$
The definition of the global integral as above is preserved by these gauge transformations. This is the whole point of the construction: if we had only integrated the ##(L_{p+1})_i## over the cells of the triangulation without the contributions of the gluing forms ##(\kappa_{\bullet})##, then the resulting sum would not be invariant under the operation of shifting the Lagrangians by horizontally exact terms (“total derivatives”) ##L_i \mapsto L_i + d_H \rho_i##.
It might seem that this solves the problem. But there is one more subtlety: if the action functional takes values in the real numbers, then the functions assigned to ##(p+2)##-fold intersections of patches are real valued, and then one may show that there exists a gauge transformation as above that collapses the whole system of forms back to one globally defined Lagrangian form after all. In other words: requiring a globally well-defined ##\mathbb{R}##-valued action functional forces the field theory to be globally variational, and hence rules out all locally variational field theories, such as those of higher WZW-type.
But there is a simple way to relax the assumptions such that this restrictive conclusion is evaded. Namely we may pick a discrete subgroup ##\Gamma \subset \mathbb{R}## and relax the condition on the functions ##(\kappa_0)_{i_0 \cdots i_{p+1}}## on ##(p+2)## fold intersections to the demand that on ##(p+3)##-fold intersections their alternating sum vanishes only modulo ##\Gamma##. A system of ##(p+2)-k##-forms on ##k##-fold intersections with functions regarded modulo ##\Gamma## this way is called a (horizontal) ##\mathbb{R}/\mathbb{Z}##-Cech-Deligne cocycle in degree ##(p+2)##.
For instance, for field theories of WZW-type with WZW curvature ##\omega##, we may take ##\Gamma## to be the discrete group of periods of the closed-form ##\omega##. Then one may show that a lift of ##\omega## to a Cech-Deligne cocycle of local Lagrangians with gluing data always exists. Indeed in general more than one inequivalent lift exists. The choice of these lifts is a choice of prequantization.
However, modding out a discrete subgroup ##\Gamma## this way also affects the induced global integral: that integral itself is now only defined modulo the subgroup ##\Gamma##:
$$
S(\phi) = \int_{\Sigma} j^\infty(\phi)^\ast(\{(L_{(p+1)})_i\},\, \{(\kappa_{p})_{i j}\}, \cdots) \;\;\;\; \in \mathbb{R}/\Gamma
\,.
$$
Now, there are not that many discrete subgroups of ##\mathbb{R}##. There are the subgroups isomorphic to the integers, and then there are dense subgroups, which make the quotient ##\mathbb{R}/\Gamma## ill-behaved. Hence we focus on the subgroup of integers.
The space of group inclusions ##i : \mathbb{Z} \longrightarrow \mathbb{R}## is parameterized by a non-vanishing real number ##2\pi \hbar \in \mathbb{R}-\{0\}##, given by ##i : n \mapsto 2\pi \hbar n##. The resulting quotient ##\mathbb{R}/_{\!\hbar}\mathbb{Z}## is isomorphic to the circle group ##SO(2)\simeq U(1)##, exhibited by the short exact exponential sequence
$$
0
\to
\mathbb{Z}
\stackrel{2 \pi \hbar \cdot (-)}{\longrightarrow}
\mathbb{R} \stackrel{\exp(\tfrac{i}{\hbar}(-))}{\longrightarrow}
U(1)
\to 0 \,.
$$
Hence in the case that we take ##\Gamma := \mathbb{Z}##, then we get locally variational field theories whose action functional is well-defined modulo ##2\pi\hbar##. Equivalently the exponentiated action functional is well defined as a function with values in ##U(1)##:
$$
\exp(\tfrac{i}{\hbar}S(\phi)) \; \in \; U(1) \simeq \mathbb{R}/_{\!\hbar}\mathbb{Z}
\,.
$$
The appearance of Planck’s constant ##\hbar## here signifies that requiring a locally variational classical field theory to have a globally well-defined action functional is related to preparing it for quantization. Indeed, if we consider the above discussion for ##p= 0##, then the above construction reproduces equivalently Kostant-Souriau’s concept of geometric pre-quantization. Accordingly we may think of the Cech-Deligne cocycle data ##(\{U_i\};\{(L_{p+1})_i\}, \{(\kappa_p)_{i j}\},\cdots)## for general ##p## as encoding higher pre-quantum geometry.
Coming back to the formulation of variational calculus in terms of diagrammatics in the sheaf topos ##\mathrm{Sh}(\mathrm{PDE}_\Sigma)## as in the previous article, what we, therefore, are after is a context in which the moduli object ##\mathbf{\Omega}^{p+1}_H## of globally defined horizontal ##(p+1)##-forms may be promoted to an object which we are going to denote ##\mathbf{B}^{p+1}_H(\mathbb{R}/_{\!\hbar}\mathbb{Z})_{\mathrm{conn}}## and which modulates horizontal Cech-Deligne cocycles, as above.
Standard facts in homological algebra and sheaf cohomology say that in order to achieve this we are to pass from the category of sheaves on ##\mathrm{PDE}_\Sigma## to the “derived category” over ##\mathrm{PDE}_\Sigma##. We may take this to be the category of chain complexes of sheaves, regarded as a homotopy theory by understanding that a morphism of sheaves of chain complexes that is locally a quasi-isomorphism counts as a weak equivalence. In fact, we may pass a bit further. Using the Dold-Kan correspondence to identify chain complexes in non-negative degree with simplicial abelian groups, hence with group objects in Kan complexes, we think of sheaves of chain complexes as special cases of sheaves of Kan complexes [Brown 73]:
$$
\mathrm{Sh}(\mathrm{PDE}_\Sigma, \mathrm{ChainCplx})
\stackrel{\mathrm{Dold-Kan}}{\longrightarrow}
\mathrm{Sh}(\mathrm{PDE}_\Sigma,\mathrm{KanCplx})
\simeq
\mathrm{Sh}_\infty(\mathrm{PDE}_\Sigma)
\,.
$$
For lecture notes with details on how all this works see
- geometry of physics — homotopy types
- geometry of physics — smooth homotopy types
In such a homotopy-theoretically enlarged context we find the sheaf of chain complexes that is the ##(p+1)##-truncated de Rham complex with the integers included into the 0-forms:
$$
\mathbf{B}^{p+1}_H( \mathbb{R}/_{\!\hbar}\mathbb{Z})_{\mathrm{conn}}
:=
[\mathbb{Z} \stackrel{2\pi \hbar}{\to} \mathbf{\Omega}^0_H \stackrel{d_H}{\to} \mathbf{\Omega}^1_H \stackrel{d_H}{\to} \cdots \stackrel{d_H}{\to}\mathbf{\Omega}^{p+1}_H]
\,.
$$
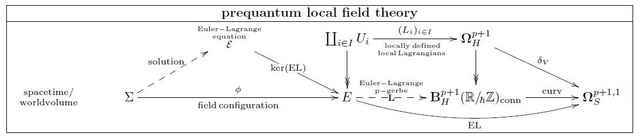
This chain complex of sheaves is known as the (horizontal) Deligne complex in degree ##(p+2)##. The horizontal Cech-Deligne cocycles that we saw before are exactly the cocycles in the sheaf hypercohomology with coefficients in the horizontal Deligne complex. Diagrammatically in ##\mathrm{Sh}_\infty(\mathrm{PDE}_\Sigma)## these are simply morphisms ##\mathbf{L} : E \to \mathbf{B}^{p+1}(\mathbb{R}/_{\!\hbar}\mathbb{Z})## from the field bundle to the Deligne moduli:
$$
\left\{\{U_i\}, \{(L_{p+1})_i\}, \{(\kappa_p)_{i j}\}, \cdots \right\}
\;\;\;
\simeq
\;\;\;
\left\{
E \stackrel{\mathbf{L}}{\longrightarrow} \mathbf{B}^{p+1}_H( \mathbb{R}/_{\!\hbar}\mathbb{Z})_{\mathrm{conn}}
\right\}
\,.
$$
This is such that a smooth homotopy between two maps to the Deligne moduli is equivalently a coboundary of Cech cocycles:
Evidently, the diagrammatics serves as a considerable compression of data. In the following all diagrams we displays are filled with homotopies as on the right, even if we do not always make them notationally explicit.
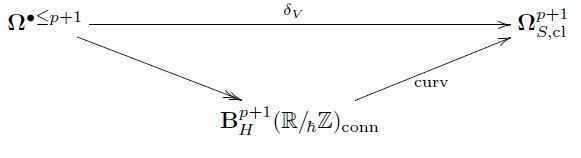
There is an evident morphism ##\mathbf{\Omega}^{p+1}_{H} \longrightarrow \mathbf{B}^{p+1}_H( \mathbb{R}/_{\!\hbar}\mathbb{Z})_{\mathrm{conn}}## which includes the globally defined horizontal forms into the horizontal Cech-Deligne cocycles (regarding them as Cech-Deligne cocycles with all the gluing data ##(\kappa_\bullet)## vanishing). This morphism turns out to be the analog of a covering map in traditional differential geometry, it is an atlas of smooth stacks:
Via this atlas, the Euler variational differential ##\delta_V## on horizontal forms that we have seen in the previous article extends to horizontal Deligne coefficients to induce a curvature map on these coefficients.
A prequantization of a source form ##\mathrm{EL}## is a lift through this curvature map, hence a horizontal Cech-Deligne cocycle ##\mathbf{L}## of locally defined local Lagrangians for ##\mathrm{EL}##, equipped with gluing data:
In summary, comparing this to the diagrammatics for variational and locally variational classical field theory which we discussed in the previous article, we have the following three levels of description of local Lagrangian field theory:
In analogy to how the integral of such an “Euler-Lagrange ##p##-gerbe” ##\mathbf{L}## over ##\Sigma## gives a globally well-defined function on field configurations, so the integral over ##\mathbf{L}## over a codimension-1 (Cauchy-)surface will give a “globally well-defined 1-form”, namely a connection, on the space of classical field configurations. This turns out to be a prequantization of the covariant phase space. This we turn to in the next article.
I am a researcher in the department Algebra, Geometry and Mathematical Physics of the Institute of Mathematics at the Czech Academy of the Sciences (CAS) in Prague.
Presently I am on leave at the Max Planck Institute for Mathematics in Bonn.


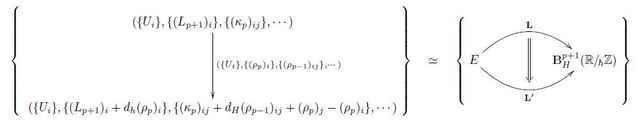








[QUOTE=”David Corfield, post: 5253766, member: 573332″]I see the Anderson you mentioned above has moved into [URL=’http://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=1000&context=dg_pres’]computer techniques[/URL] for differential geometry.[/QUOTE]
Yes, apparently he has said that his interest in this computer algebra is what prevented him from fully finalizing his book on the variational bicomplex.
[QUOTE=”David Corfield, post: 5253766, member: 573332″]That might provide a point of comparison if you succeed in encouraging people to implement modal homotopy type theory.[/QUOTE]
I feel that eventually there will be a considerable gain in having computer support not only for the tensor calculus representation of variational calculus (and ultimately of prequantum field theory) but also of its conceptual structure. For instance, as the next article in the series will discuss, Noether’s variational theorem has a more fundamental representation than the usual component-derivation, and algebra software that could handle differential cohesion would be able to reason about this. But then, presently this is apparently a topic too far in the future. We’ll see.
On a different note, I have added to the entry above a paragraph which makes explicit that homotopies between maps into the Deligne moduli ##mathbf{B}_H^{p+1}(mathbb{R}/_{!hbar}mathbb{Z})_{mathrm{conn}}## are equivalently coboundaries between the corresponding Cech-Deligne cocycles. I’ll be using this a lot in article number V in the series, and so I went back and made it more explicit here.
I see the Anderson you mentioned above has moved into [URL=’http://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=1000&context=dg_pres’]computer techniques[/URL] for differential geometry. That might provide a point of comparison if you succeed in encouraging people to implement modal homotopy type theory.
Regarding Butterfield’s points, ah, maybe I numbered them in the wrong order, true. In either case, I am not sure if I recognize the “necessary in nearby possible worlds”-modality in his text, but I still think and agree that this may be a fun way to think of the jet comonad as being about infintiesimal necessity and as the shell as being a modal type for that modality.
(Now of course nobody following us here will know what we are talking about, so maybe I should close with adding that this is about the analogy of the [URL=’http://ncatlab.org/nlab/show/jet comonad’]jet comonad[/URL] to the [URL=’http://ncatlab.org/nlab/show/necessity+and+possibility#InFirstOrderLogicAndTypeTheory’]necessity modality[/URL].)
Regarding worked examples: there is standard literature, [URL=’http://ncatlab.org/nlab/show/variational%20bicomplex#Anderson89′]Anderson’s book[/URL] is really good
Good, point, I have started an nLab entry [URL=’http://ncatlab.org/nlab/show/shell’][I]shell[/I][/URL]. Does the text there now answer your question?
So we could do with an nLab entry on ‘shell’. At the moment we just have “[URL=’http://ncatlab.org/nlab/show/off-shell+Poisson+bracket’]off-shell Poisson bracket[/URL]’ and ”[URL=’http://ncatlab.org/nlab/show/on-shell+recursion’]on-shell recursion[/URL]’. You’re saying the shell is the critical locus of the EL-functional.
Hmm, I see there are some basics I haven’t sorted out. Why doesn’t the process of finding the critical locus deliver a subspace of $[Sigma, E]$? Instead we have solutions as $[Sigma, mathcal{E}]$ where $mathcal{E}$ is a subspace of $E$. And this $mathcal{E}$ is said to be an equation. Presumably there’s the employment of equivalences, such as when a differential equation is identified with its space of solutions, but I’m still struggling with what $mathcal{E}$ is if it’s also a subspace of $E$. Is there a simplest example of a classical field to work through?
[QUOTE=”David Corfield, post: 5251128, member: 573332″]One day I mean to take another look at [URL]http://arxiv.org/abs/physics/0210081[/URL] to see whether the modality of classical mechanics there matches your ideas.[/QUOTE]
It seems to me that the use of the word “modality” there is more vague than what is used in [URL=’http://ncatlab.org/schreiber/show/Modern+Physics+formalized+in+Modal+Homotopy+Type+Theory’][I]Modern physics formalized in Modal homotopy type theory[/I][/URL] . In any case, on pages 12-13 of [URL=’http://arxiv.org/abs/physics/0210081′]physics/0210081[/URL] there is the following, in brief summary and in my (re-)formulation:
[LIST]
[*]his 1st modality is about the question: to which extent does the whole field bundle ##E## matters beyond the critical locus (the physical shell) ##mathcal{E}## inside it
[*]his 2nd modality refers to field bundles ##E## which may not describe anything seen in nature;
[*]his 3rd modality refers to Lagrangians ##L## which may not describe anything seen in nature.
[/LIST]
The second and third issue is the one of concrete particulars of general abstract theories. The question is: once we have the fundamental theory of nature (such as Einstein-Maxwell-Yang-Mills-Dirac-Higgs theory) are there models (“vacua”) that are somehow singled out as being really realized. See also our discussion re “[URL=’http://ncatlab.org/nlab/show/universal+exceptionalism’]universal exceptionalism[/URL]”, the [URL=’http://ncatlab.org/schreiber/show/Modern+Physics+formalized+in+Modal+Homotopy+Type+Theory#nature’]brane bouquet[/URL], etc.
The first relates more to a concrete technical question. In the next article in the series I describe how one needs to lift the “Euler-Lagrange##p##-gerbe” to a “Lepage ##p##-gerbe” and then restrict that to the shell. The lift needs to happen off-shell, and so it’s indeed a good question how much of a neighbourhood of the classical shell one needs to take into account for the lift.
The same kind of issue appears in Noether’s theorem, where one considers symmetries that must be defineable off-shell but in the end are only considered in their restriction on shell.
In the end this has to do with the question to which extent the path integral may be substituted by (or rather: be made rigorous by) constructions that happen just on the covariant phase space: the path integral by definition integrates over all sections of ##E##, not just those of the shell. The covariant phase space however is just the shell ##mathcal{E}## equipped with some prequantum information ##mathbf{Theta}## about how it deforms into ##E##. There is a somewhat subtle question here as to how much of the original ##E## is seen by ##(mathcal{E},mathbf{Theta})##.
That's helpful, thanks. Returning to Butterfield's text, regarding his modality type 2, " it considers a counterfactual number of degrees of freedom, or a counterfactual potential function," wouldn't that include varying the Lagrangian, which you have above as type 3?His 3rd type, as I read it, sounds like looking off-shell. " the counterfactual histories share the initial and final conditions, but do not obey the given deterministic laws of motion, with the given forces." Since we may be able to change the Lagrangian to make one of these non-legal trajectories into a legal trajectory for the new Lagrangian, he says " I also agree that my distinction between (Modality;3rd) and (Modality;2nd), between varying the laws and varying the forces, is not as hard-and-fast as it first seems"His type 1 is just shifting through the solution space by varying initial conditions.So what you call modality type 1 (which I think is Butterfield's type 3) might be construed in terms of infinitesimal invariance around the shell, so link to the kind of jet comonad modality we've discussed?
One day I mean to take another look at http://arxiv.org/abs/physics/0210081 to see whether the modality of classical mechanics there matches your ideas.