Understanding Zero: History, Division, Exponents, 0!

The goal of this FAQ is to clarify the concept of 0, and specifically the operations that are allowed with it.

The best way to start this FAQ is to look at a bit of history.

A short history of 0

Historically, there are two different uses of zero: zero as a placeholder and zero as a number in its own right. Zero is used as a placeholder in numbers such as 1010. It merely indicates that the first 1 stands for a thousand and that the second 1 stands for ten. If we didn’t have a placeholder zero, then we couldn’t differentiate between 11 and 1010. So zero is just a symbol here and does not have any particular meaning.

Zero as a number is a much more controversial topic. It asserts that zero is a number in its own right and has the same privileges as 1, 2, 3, 4, etc. Nowadays, zero is a well-respected number, but that wasn’t always the case.

It didn’t even always exist as a placeholder. For example, the Babylonians couldn’t differentiate between numbers such as 8 and 80. Nevertheless, people soon saw the difficulty and started using a placeholder anyway. Our concept of “zero” as both a placeholder and a number originated in India in the 9th century. However, mathematicians were quite unsure about how to work with zero.

For example, some rules involving zero were:

• A number when divided by 0 is a fraction with 0 in the denominator.
• Zero divided by zero is zero.
• As we shall soon see, these rules are not used in practice today.

The Indian mathematical knowledge soon found its way to the Arabs. Specifically, al-Khwarizmi popularized the Hindu numeral system. The Arab knowledge found its way into Europe by Fibonacci. By the 16th century, the Hindu numerals (including zero) were in use throughout Europe.

For more information about this fascinating topic, see: http://www.gap-system.org/~history/HistTopics/Zero.html

Is zero positive or negative?

By definition, zero is neither positive nor negative. The positive numbers are the numbers x such that x>0. The negative numbers are the numbers x such that x<0. So 0 is neither positive nor negative. We also say that 0 has no sign. This is true by definition, so other definitions could be used but they are not standard.

Zero is also both nonnegative and nonpositive.

Operations with zero

Zero is known as the additive identity: for every number x (that is: x can be natural, real, complex, etc.) we have $x+0=x=0+x$.

From this, we can easily infer what 0x is (by using distributivity):

$$0x=(0+0)x=0x+0x~\Rightarrow~0x=0$$

So 0 times anything is 0. (This holds in every ring.)

The division is a bit more difficult. First, we must define what division is. We say that $\frac{a}{b}=c$ if and only if c is the unique number such that a=bc.

From this, we can infer that $\frac{0}{x}=0$ for each nonzero x. To show this, we need to prove that 0x=0 and that there is no other number c such that cx=0. The former is proven above. The latter is also true (for nonzero x), but it might not be obvious why. To prove this, we need to know what exactly multiplication is. This requires knowledge of the Peano axioms and so on. Therefore, we will leave this for another FAQ.

Division by 0

Now, what if 0 is the denominator? That is, what if we have $\frac{x}{0}$ or even $\frac{0}{0}$? In this case, we say that the division is undefined. Indeed, if x is nonzero, then there is no number c such that $\frac{x}{0}=c$. That is, there is no c such that 0c=x. We have shown that 0 times any number is 0, so 0c can never be a nonzero number x.

This argument fails when x=0. In that case, there are numbers c such that 0c=0. The problem is that these numbers are not unique: all numbers satisfy 0c=0. So $\frac{0}{0}$ would equal every number. This is undesirable, so we leave $\frac{0}{0}$ undefined.

Some say that $\frac{x}{0}=\infty$. First of all, $\infty$ is not a number in the usual sense, so saying $\frac{x}{0}=\infty$ is not acceptable unless we have extended the number system to include infinity.

Of course, it is possible to extend our number system to include $+\infty$ and $-\infty$. This is the context of the extended real numbers (see http://en.wikipedia.org/wiki/Extended_real_number_line). Even then, defining division by 0 remains undesirable. To see why consider the graph of $1/x$.

The graph of $1/x$ becomes very large in magnitude when x is close to 0. If we approach 0 from the right, $1/x$ tends to $+\infty$; if we approach from the left, $1/x$ tends to $-\infty$. Because the one-sided limits differ, we cannot assign a single infinite value to $\frac{1}{0}$, and this is why we leave $\frac{1}{0}$ undefined.

There is, however, a different number system where $+\infty=-\infty$. That system is the projective real line (see Real projective line), in which there is a single point at infinity denoted $\infty$. In that context one can define $\frac{x}{0}=\infty$, but $\frac{0}{0}$ remains undefined because there is no unique c with 0c=0.

Exponentiation and 0

Exponentiation with 0 is another subtle topic. Recall that if n is a nonzero natural number, then we define $a^n=a*a*a*…*a$, multiplying a with itself n times. But how should we give sense to $a^0$?

To formulate a sensible definition, we first use the law $a^{n+m}=a^na^m$, which holds for all nonzero naturals n and m. We would like it to hold when one exponent is 0 as well. That gives

$$a^m=a^{0+m}=a^0a^m$$

so $a^0$ must be a number with $ba^0=b=a^0b$ for all b. Thus $a^0$ must be the multiplicative identity, and we define $a^0=1$ for nonzero a.

The problematic case is $0^0$. Defining $0^0=1$ is consistent with the algebraic convention above, but it produces functions such as $f(x)=0^x$ that are zero for all x≠0 and equal to 1 at x=0, which is discontinuous. The two-variable map $f(x,y)=x^y$ likewise has an essential singularity at (0,0), suggesting that $0^0$ could be assigned different values depending on context. For these reasons many sources leave $0^0$ undefined.

However, many mathematicians adopt the convention $0^0=1$ because it is convenient and does not break common combinatorial formulas. For example, the binomial theorem

$$(x+y)^n=\sum_{k=0}^n{\binom{n}{k}x^ky^{n-k}}$$

is valid in full generality if one sets $0^0=1$, since otherwise terms with x=0 and n=0 become problematic.

Factorials and 0

Factorials behave more cleanly: we can define 0! in a consistent way that fits all standard conventions. Consider the recursive definition:

$$1!=1~\text{and}~(n+1)!=(n+1)*n!$$

Applying the recursion with n=0 gives

$$1!=1*0!$$

so defining 0!=1 is natural.

The factorial also has a combinatorial interpretation: n! is the number of ways to order n objects. For example, there are 3!=6 permutations of {a,b,c}:

$$(a,b,c),~(a,c,b),~(b,a,c),~(b,c,a),~(c,a,b),~(c,b,a)$$

There are 2!=2 permutations of {a,b}, 1!=1 permutation of {a}, and 0!=1 way to order the empty set, which is the empty sequence. The factorial n! also equals the number of bijections $f:\{1,…,n\}\rightarrow\{1,…,n\}$; there is exactly one bijection $f:\emptyset\rightarrow\emptyset$, namely the empty function.

Factorials appear in binomial coefficients defined by

$$\binom{n}{k}=\frac{n!}{k!(n-k)!}$$

This counts the ways to choose k elements from n elements where order does not matter. For example,

[tex]\binom{4}{2}=6[/tex>

which corresponds to the six 2-element subsets of {a,b,c,d}.

What happens when k=n? We should get the number of ways to choose n elements from n elements, which is 1. Thus $\binom{n}{n}$ equals 1. If k=0, choosing zero elements also has exactly one outcome (the empty selection), and

$$\binom{n}{0}=\frac{n!}{0!n!}=1$$

The binomial theorem and many combinatorial identities work uniformly if we define 0!=1.

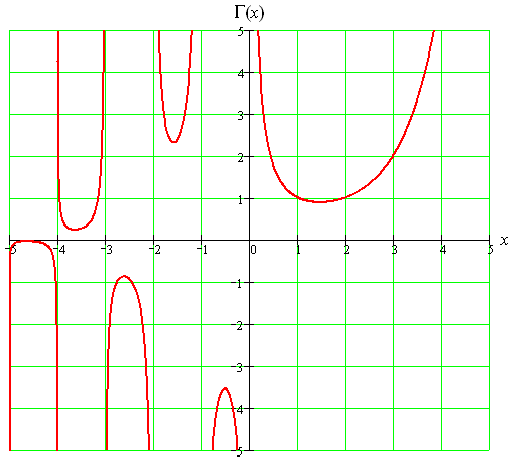
Analytically, the Gamma function provides a continuous extension of the factorial:

$$\Gamma(z)=\int_0^{+\infty}{t^{z-1}e^{-t}dt}$$

and it satisfies $$\Gamma(n)=(n-1)!$$. Thus

$$0!=\Gamma(1)=1$$

All this evidence supports the conventional definition 0!=1. There is no analogous universally satisfactory definition for $0^0$.

The following forum members have contributed to this FAQ:

• Borek
• D H
• HallsOfIvy
• Hootenanny
• Mark44
• micromass
• tiny-tim

Link to the forum post