The History and Importance of the Riemann Hypothesis

Riemann Hypothesis History

The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field of number theory. It’s named after the German mathematician Bernhard Riemann, who introduced the hypothesis in 1859.

• RH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line.
• ERH: All zeros of L-functions to complex Dirichlet characters of finite cyclic groups within the critical strip lie on the critical line.
• Related Article: The Extended Riemann Hypothesis and Ramanujan’s Sum: Shortest Possible Explanation

The history of the Riemann hypothesis may be considered to start with the first mention of prime numbers in the Rhind Mathematical Papyrus around 1550 BC. It certainly began with the first treatise of prime numbers in Euclid’s Elements in the 3rd century BC. It came to a – hopefully temporary – end on the 8th of August 1900 on the list of Hilbert’s famous problems. And primes are the reason why we are more than ever interested in the question of whether ERH holds or not. For e.g. the RSA encryption algorithm (Rivest-Shamir-Adleman, 1977) relies on the complexity of the factorization problem FP, that it is NP-hard. FP is probably neither NP-complete nor in P but we do not know for sure. Early factorization algorithms that ran in a reasonable time had to assume the extended Riemann hypothesis (Lenstra, 1988, [1]). So what do prime numbers have in common with the Riemann hypothesis which is about a function defined as a Dirichlet series?
$$
\zeta(s)=\sum_{n=1}^\infty \dfrac{1}{n^s}
$$
One has to admit that what we call prime number theory today originated in the 19th century when Dirichlet began in 1837 to apply analysis to number theory. There is a large gap between Euclid and Euler who published a new proof for the infinite number of primes in 1737.

Prime Numbers

A short answer would be that
$$
\zeta(s)=\sum_{n=1}^\infty \dfrac{1}{n^s}=\prod_{p\text{ prime}}\dfrac{1}{1-{p}^{-s}}.
$$
This is easy to prove [5] but falls a bit short of the relationship between prime numbers and the Riemann hypothesis. E.g. the basic idea for our example of why FP can be solved quickly under the assumption of ERH is, that ERH implies the existence of relatively small primes which then can be found by fast algorithms. (See the theorems of Ankeney/Montgomery/Bach, Miller, Bach [10] and the references therein.)

Let $1/2 \leq \theta \leq 1.$ Then

$$\large{\operatorname{RH}(\theta)\, : \,\zeta(s) \text{ has no zeros in }\{\mathfrak{R}(s)>\theta\}}$$

is another generalization of the Riemann hypothesis. The original Riemann hypothesis is thus $\operatorname{RH}(1/2)$ and we know there are no zeros of the zeta-function in $\{\mathfrak{R}(s)>1\}$. So $\operatorname{RH}(1)$ is true, but no proof is known for values of $\theta$ below. We do know ([7],[8],[9]) that
$$
\large{\operatorname{RH}(\theta)\quad \Longleftrightarrow\quad \pi(x)=\operatorname{Li}(x) + O\left(x^{\theta +\varepsilon }\right)\text{ for all }\varepsilon >0}
$$
where $\operatorname{Li}(x)=\displaystyle{\int_2^x \dfrac{dt}{\log t}}$ is the integral logarithm and $\pi(x)=\left|\{p\in \mathbb{P}\,|\,p\leq x\}\right|$ the prime number function (graphic from [2]). Hence ERH is connected to the question: Where are the primes?

 

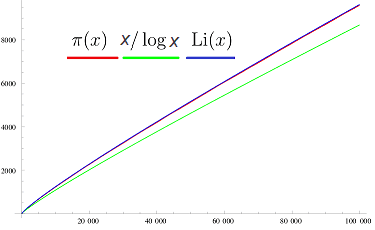
The prime number theorem
$$
\lim_{x \to \infty}\dfrac{\pi(x)}{\dfrac{x}{\log(x)}}=1
$$
was first conjectured by Gauß in 1792, however, proven by Hadamard and de la Vallée-Poussin independently a hundred years later in 1896. Their proofs were of function theoretical nature and relied on the relation of primes to the Riemannian $\zeta$-function which was first considered by Euler in the 18th century.

Another interesting equivalent formulation of $\operatorname{RH}(\theta)$ is the following: Let $a_{even}$ be the number of integers below $x>0$ that are a product of an even number of primes, and $a_{odd}$ be the number of integers below $x>0$ that is a product of an odd number of primes, then
$$
\large{\operatorname{RH}(\theta)\quad \Longleftrightarrow\quad a_{even}(x)-a_{odd}(x) = O\left(x^{\theta +\varepsilon }\right)\text{ for all }\varepsilon >0.}
$$
These two equations show that the Riemann hypothesis is not only about a Dirichlet series, or the safety of some encryption algorithms. It is why I said it all began with the notion of prime numbers. We simply want to know how prime numbers are distributed. History shows that we are fascinated by prime numbers. The Riemann hypothesis $\operatorname{RH}(1/2)$ is meanwhile checked for the first $10,000,000,000,000$ zeros of the $\zeta$-function [11], i.e. any other result than its truth would be more than surprising. In the end, we can check as many zeros as our computers can handle, it will never be a proof. However, these results above marked a huge step in the theory of prime numbers. It wasn’t long before when Euler (1707 – 1783) wrote:

“Mathematicians have hitherto strove in vain to discover any order in the sequence of prime numbers, and one is inclined to believe that this is a mystery which the human mind will never fathom. To convince oneself of this, one need only glance at the prime number tables, which some have taken the trouble to extend to 100,000, and one will at first notice that there is no order, no rule to be observed.” [12]

Early Glory

Riemann’s conjecture was only incidentally mentioned by Riemann himself, and not explicitly identified as an important problem. Riemann wrote about the zeros:

“In fact, one finds many roots within these limits, and it is very probable that all the roots are there. Of course, a rigorous proof of this would be desirable; however, after a few unsuccessful attempts, I have left the search for it aside for the time being, since it seems unnecessary for the purpose of my investigation.”

Nevertheless, he has proven that there are infinitely many roots $s$ of the $\zeta$-function with $\mathfrak{R}(s)=1/2$ and that almost all roots are close to the critical line. Siegel has discovered these proofs in 1935 when he investigated Riemann’s estate. Riemann never published them. It was Hardy 1914 who first published a proof that there are infinitely many zeros on the critical line. A little later 1921, Hardy and Littlewood proved that there is a constant $A>0$ such that there are more than $AT$ zeros with real part $1/2$ whose (absolute) imaginary part is smaller than $T.$ It follows that there is a non-zero percentage $B$ of zeros on the critical line. Levinson showed in 1974 that $B>1/3.$

It is not quite clear whether Hardy believed in God or was just superstitious. However, in any case, he believed God will do everything to make his life tough and complicated. One day, he was on a journey back home from a meeting with Harald Bohr (Niels Bohr’s brother) in Copenhagen. He had to take a ship and the boat he got didn’t look very trustful. Typically, he thought, why me?
So he sent a postcard before boarding to Bohr claiming he has found the proof of Riemann’s hypothesis. When asked afterward, why, he replied: Well, if the ship sank the proof would have been lost but I would have become the most famous mathematician of my generation. God won’t allow this to happen. That way I only had to write Bohr another postcard in which I revealed to have made a mistake.

This anecdote and data demonstrate how famous the Riemann hypothesis was already at the beginning of the last century despite Riemann’s indifference to the problem that since carries his name.

Hilbert had been invited to give a lecture at the second international congress of mathematicians in August 1900 in Paris. He decided not to give a lecture in which he would report and appreciate what had been achieved in mathematics so far, nor to respond to Henri Poincaré’s lecture at the first international congress of mathematicians in 1897 on the relationship between mathematics and physics. Instead, his lecture was intended to offer a kind of programmatic outlook on future mathematics in the coming century. This objective is expressed in his introductory words:

“Who among us would not like to lift the veil that hides the future, to have a look at the forthcoming advances of our science and into the mysteries of its development during the centuries to come! What particular goals will it be that the leading mathematical minds of generations to come will aspire to? What new methods and new facts will the new centuries discover in the vast and rich field of mathematical thought?”

He, therefore, took the congress as an opportunity to compile a thematically diverse list of unsolved mathematical problems. As early as December 1899 he began to think about the subject. At the beginning of the new year, he then asked his close friends Hermann Minkowski and Adolf Hurwitz for suggestions as to which areas a corresponding lecture should cover; both read the manuscript and commented on it before the lecture. However, Hilbert only finally wrote down his list immediately before the congress – which is why it does not yet appear in the official congress program. The lecture was originally supposed to be given at the opening, but Hilbert was still working on it at the time. Now they are known as Hilbert’s 23 problems. There has been found a 24th in his estate: “How can the simplicity of a mathematical proof be measured, and how can its minimum be found?”, but the official count is 23. They are in part very specific like the first one: “Prove the continuum hypothesis.” even if obviously not necessarily solvable, or very vague like the sixth one: “Mathematical treatment of the axioms of physics.” Here we are interested in the eighth: Prove the Riemann hypothesis, the Goldbach conjecture, and the twin prime conjecture. [3]

“Recently, significant advances have been made in the theory of the distribution of prime numbers by Hadamard, de La Vallee-Poussin, V. Mangoldt, and others. However, in order to completely solve the problems posed by Riemann’s treatise ‘On the Number of Primes Below a Given Size’, it is still necessary to prove the correctness of Riemann’s extremely important claim that the zeros of the function $\zeta(s)$, which is defined by the series $\zeta (s)=1+\frac{1}{2^{s}}+\frac{1}{3^{s}}+\cdots$, all have the real components $1/2$ if one disregards the well-known negative integer zeros. As soon as this proof is successful, the further task would be to examine the Riemann infinite series for the number of primes more precisely and in particular to decide whether the difference between the number of primes below a magnitude and the integral logarithm of $x$ becomes in fact no higher than the $\tfrac{1}{2}$th order in $x$ at infinity, and further, whether those from the first complex zeros of the function $\zeta (s)$ dependent terms of Riemann’s formula really cause the local compression of the prime numbers, which one noticed when counting the prime numbers.” [13]

Yes, language was a different one a century ago. Hilbert himself classified the Riemann hypothesis as less difficult than, for example, the Fermat problem: in a lecture in 1919 he expressed the hope that a proof would be found in his lifetime, in the case of the Fermat conjecture perhaps in the lifetime of the youngest listeners; he considered the transcendence proofs in his 7th problem to be the most difficult – a problem that was solved in the 1930s by Gelfond and Theodor Schneider. The Fermat problem was solved in 1995 by Andrew Wiles and Richard Taylor as part of their proof of the modularity theorem. A proof that is not only rather long but also rather technical and complicated, so the comparison with the Riemann hypothesis is possibly not as far-fetched as it may sound.

“If I were to awaken after having slept for a thousand years, my first question would be: Has the Riemann hypothesis been proven?” (David Hilbert) [6]

Randomness

Let’s summarize the central limit theorem of probability theory by considering a fair coin toss and we pay +1 for heads and cash in -1 for tails. The famous gambler’s fallacy is to believe that after a long straight of heads a tail would become more likely. This is wrong because randomness has no memory. Chances are still fifty-fifty. Even our overall gain or loss $L(n)$ after $n$ tosses isn’t zero. It is as unlikely that there will be exactly the same number of heads as there are tails as it is that all tosses would be heads. However, it can be proven that the probability distribution of $L(n)$ converges pointwise to a normal distribution, in our case the standard normal distribution which is the statement of the central limit theorem.

We have actually already seen the connection between the Riemann hypothesis and randomness
$$
\operatorname{RH}(\theta)\quad \Longleftrightarrow\quad a_{even}(n)-a_{odd}(n) = O\left(n^{\theta +\varepsilon }\right)\text{ for all }\varepsilon >0.
$$
Let us consider the Liouville function $\lambda (n)=(-1)^{\#\text{ prime factors of }n}$ and remember that $a_{even/odd}(n)$ counted the number of integers below $n$ that are a product of an even/odd number of primes. Then
$$
L(n)=\sum_{k=1}^n \lambda (k)= a_{even}-a_{odd}
$$
and the central limit theorem says
$$
\lim_{n \to \infty}\dfrac{L(n)}{n^{\varepsilon +1/2}}=0 \text{ for all }\varepsilon >0 \Leftrightarrow L(n)=O(n^{\varepsilon +1/2})
\Leftrightarrow RH(1/2)$$
This means that the pseudo-randomness of the distribution of prime numbers is almost independent and identical, i.e. truly random. It seems, Euler was right once more.

Number Theory

We already mentioned the fascination with prime numbers and their central meaning in number theory. It is no coincidence that there are three famous problems listed under Hilbert’s 8th problem:

1. Riemann Hypothesis
   $a_{even}(n)-a_{odd}(n)=O(n^{\varepsilon +1/2})$
2. Goldbach’s Conjecture
   Every even integer greater than $2$ is the sum of two primes.
3. Twin Prime Conjecture
   There are infinitely many pairs $(p,p+2)$ of prime numbers $p.$

Neither of these conjectures are proven although they have been tested for incredibly large amounts of numbers computationally. They all have to do with prime numbers. An integer $p$ is prime, if and only if $(p-1)!\equiv -1 {\pmod p}$ (Wilson’s theorem), and a pair $(p,p+2)$ is a pair of primes, if and only if $4\cdot ((p-1)!+1)+p \equiv 0 {\pmod {p\cdot (p+2)}}$ (Clement’s theorem).

Goldbach’s conjecture or the strong Goldbach conjecture has a weaker version: Every odd number greater than $5$ is the sum of three primes. Since $3$ is prime and $2n+1=2n-2+3=p+q+3,$ the strong version implies the weaker, which has been partially solved. On one hand, is it true in case the extended Riemann hypothesis holds, and on the other hand, it holds for sufficiently large numbers. If $R(n)$ is the number of representations of $n$ as the sum of three prime numbers, then (Vinogradov’s theorem)
$$
R(n)=\dfrac{n^2}{2(\log n)^3}\underbrace{\left(\prod_{p\mid n}\left(1-\dfrac{1}{(p-1)^2}\right)\right)\left(\prod_{p\nmid n}\left(1+\dfrac{1}{(p-1)^3}\right)\right)}_{=:G(n)}+O\left(\dfrac{n^2}{(\log n)^4}\right)
$$
and it can be shown that $G(2n)=0,$ $G(2n-1)\geq 1,$ and $G(2n-1)$ is asymptotically of order $O(1),$ hence $R(2n-1)>0$ for sufficiently large $n.$

Physics

There have been quite a few attempts to tackle the problem by physical methods, especially lately. This is quite surprising since mathematics is a deductive science and physics a descriptive science. One can check the results of theoretical models in a physical world, but how should real-world observations contribute to a mathematical conjecture? The origin of such a connection, however, isn’t quite new. David Hilbert and Pólya György had already noticed that the Riemann hypothesis would follow if the zeros were eigenvalues of an operator $({\tfrac{1}{ 2}}+iT)$ where $T$ is a Hermitian (i.e. self-adjoint) operator, which therefore has only real eigenvalues, similar to the Hamiltonian operators in quantum mechanics. Further considerations in this direction end up in the theory of quantum chaos. Other connections have been drawn to statistical mechanics [3], or one-dimensional quasi-crystals [15]. We even had a visitor on Physics Forums who attempted to access it via the hydrogen atom. All these thoughts are based on parallels between the Riemann hypothesis and probability distributions and are often due to similarities in formulas.

Cryptology

In addition to numerous applications in many areas of mathematics, the Riemann Hypothesis is also of interest in cryptology. For example, the RSA cryptosystem uses large prime numbers to construct both public and private keys. Its security is based on the fact that conventional computers do not yet have an efficient algorithm for dividing a number into its prime factors, i.e. to solve FP. The theory behind RSA requires only results from elementary number theory. In 1976, again based on simple number theory and using Fermat’s little theorem, Miller developed a deterministic primality test that works assuming the extended Riemann Hypothesis [16]. In 1980, Michael O. Rabin used Miller’s results to develop a probabilistic test that worked independently of the extended Riemann hypothesis [17]. Through the work of Bach in 1990, this so-called Miller-Rabin test can be converted into a deterministic test that runs with the speed $O(\log(n)^{2})$, again assuming the extended Riemann Hypothesis [10]. All the connections between the Riemann hypothesis and cryptology are at their core due to its meaning for the distribution of prime numbers.