First-Order Linear Equation: Definition & Solutions

Definition / Summary

This article summarizes the first-order (linear) polynomial equation in one variable, its solution, and natural extensions to matrices and operators.

Definition

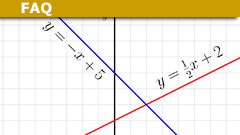
A first-order polynomial (linear) equation in one variable has the general form $$Mx + B = 0$$, where $$x$$ is the variable, $$M$$ and $$B$$ are constants, and $$M \neq 0$$.

Equation (standard form)

$$Mx + B = 0$$

Scalar solution

Because $$M \neq 0$$, the solution in the scalar (ordinary number) case is

$$x = -\dfrac{B}{M}.$$

Matrix and vector case

The variable x does not have to be a scalar number. If x and B are vectors and M is a matrix, a solution exists when the matrix is invertible. The condition for a solution to exist is

$$\det(M) \neq 0.$$

When that holds, the solution is

$$\vec{x} = -\,M^{-1}\vec{B},$$

where $$M^{-1}$$ is the matrix inverse of M.

Operator example: Green’s function for the Schrödinger equation

A more abstract example uses linear operators. Consider the Green’s function equation for the time-dependent Schrödinger equation. In that case, x is a Green’s function, B is a Dirac delta function in time, and the operator M takes the form

$$M = \left(\frac{i}{\hbar}\frac{\partial}{\partial t} – \hat{H}\right),$$

where $$\hat{H}$$ is the Hamiltonian operator.

Further reading

• Hilbert spaces and related concepts
• Operators, functionals and representations explained

Comment thread (original discussion)