John Baez Interview — Mathematical Physicist & Networks

We are proud to introduce you to Mathematical Physicist and PF member John Baez!

Give us some background on yourself

I’m interested in all kinds of mathematics and physics, so I call myself a mathematical physicist. I’m a math professor at the University of California, Riverside (UC Riverside), where I’ve taught since 1989. My wife, Lisa Raphals, joined the faculty nine years later; among other things she studies classical Chinese and Greek philosophy.

I earned my bachelor’s degree in mathematics at Princeton. For my undergrad thesis I studied whether a computer can solve Schrödinger’s equation to arbitrary accuracy. In the end it became clear that you can. I was very interested in mathematical logic and used the theory of computable functions in my thesis, but I decided it wasn’t very helpful for physics. After reading the poetic last chapter of Misner, Thorne and Wheeler’s Gravitation, I decided quantum gravity was the problem to work on.

Graduate school and early research

I went to math grad school at MIT but didn’t find anyone to work with on quantum gravity, so I did my thesis on quantum field theory with Irving Segal. He was one of the founders of constructive quantum field theory, which aims to rigorously prove that quantum field theories make mathematical sense and obey expected axioms. It was a difficult subject; I didn’t accomplish everything I hoped, but I learned a great deal.

After a postdoc at Yale I switched to classical field theory, mainly because it was something I could make progress on. On the side I continued trying to understand quantum gravity. String theory was rising in prominence, and it would have been easier to jump on that bandwagon, but much early work studied strings on a fixed background spacetime. Quantum gravity should describe a variable, quantum-mechanical geometry of spacetime, so I wasn’t comfortable with background-dependent approaches.

Loop quantum gravity, spin networks and n-categories

I obtained a professorship at UC Riverside based on my classical field theory work. At a conference in Seattle I heard Abhay Ashtekar, Chris Isham and Renate Loll give talks on loop quantum gravity. Their background-free and mathematically rigorous approach appealed to me, so I began working on loop quantum gravity.

Quantum gravity is often easier in lower dimensions. I became interested in how category theory can be used to formulate quantum gravity in three spacetime dimensions. This led to a radical conception of space where geometry is described in a thoroughly quantum-mechanical way. Ultimately, space can be a quantum superposition of “spin networks”, which resemble Feynman diagrams. Roughly speaking, a spin network represents a virtual process in which particles move and interact; if we know the likelihood of each process, we can infer the geometry of space.

A spin network

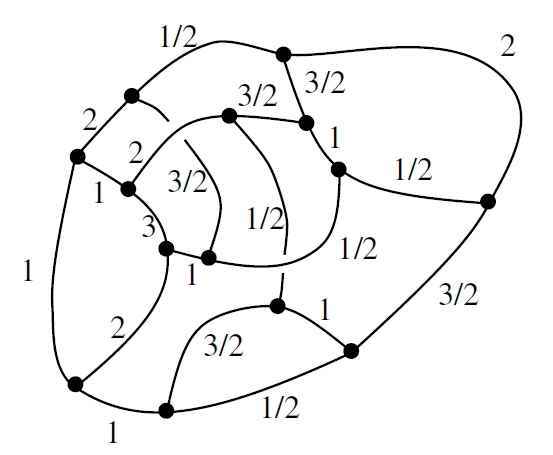
Loop quantum gravity seeks to do the same for four-dimensional quantum gravity, but it has been more challenging. Louis Crane proposed that 4-dimensional quantum gravity may require a more sophisticated structure: a “2-category”. I had not heard of 2-categories before. Category theory studies objects and processes that turn one object into another; in a 2-category there are also “meta-processes” that turn one process into another.

I became excited about 2-categories. Later James Dolan introduced me to n-categories, which opened many possibilities. He came to UC Riverside to work with me, and we began thinking about n-categories alongside loop quantum gravity.

Dolan was technically my graduate student, but I learned a lot from him. In 1996 we wrote “Higher-dimensional algebra and topological quantum field theory”, which I consider one of my best papers. It contains bold hypotheses about n-categories and their links to mathematics and physics. At the time, good definitions of n-categories existed only for n < 4, so we framed our ideas as hypotheses rather than precise conjectures. Since then many researchers have accepted and proved parts of these hypotheses. Jacob Lurie advanced one statement and provided a 111-page outline of a proof, though some foundational definitions still needed refinement.

A foam of soap bubbles

In 1997 I introduced “spin foams”, structures like spin networks but with an extra dimension. Spin networks have vertices and edges; spin foams also have 2-dimensional faces — imagine a soap-bubble foam. The idea was to use spin foams to give a purely quantum description of spacetime geometry. Mathematically, this corresponds to moving from a category to a 2-category.

Multiple spin foam theories have been proposed, but it’s unclear whether any fully succeed. In 2002 Dan Christensen, Greg Egan and I performed large-scale numerical calculations and found that the most popular spin foam model at the time produced results very different from expectations; I believe our work essentially undermined that model.

Shifts in focus: from quantum gravity to n-categories and beyond

I found that spending years testing spin foam models was unattractive to me, and I didn’t enjoy programming. Meanwhile, n-category theory was mathematically natural for me and a source of many new ideas. So I shifted my focus from quantum gravity to n-categories.

Quitting quantum gravity was emotionally difficult. It felt like leaving a “holy grail” pursuit, and many colleagues considered unifying quantum mechanics and general relativity the most important problem in physics. It took years to shift my mindset.

Ironically, leaving quantum gravity allowed me to explore string theory more freely. As a branch of mathematics it’s beautiful, and n-categories apply here as well: particles relate to categories while strings relate to 2-categories. I explored this with Urs Schreiber and John Huerta.

Around 2010 I began focusing on environmental issues and math relevant to engineering and biology for the planet’s sake. That required another painful transition. Fortunately, researchers like Urs Schreiber and others continue work on n-categories and string theory, often advancing further than I might. I follow these developments from the sidelines.

It’s likely we’ll need many more ideas before we make major progress on quantum gravity, but I remain confident that n-categories will play a role. I’m glad to have helped advance that field.

Your uncle, Albert Baez — early influence

My uncle had a huge effect on me. He’s better known as the father of folk singer Joan Baez, but he began in optics and helped invent the first X-ray microscope. Later he focused on physics education, particularly in countries then referred to as “third-world countries.” For example, in 1951 he helped establish a physics department at the University of Baghdad.

Albert V. Baez

When I was a kid he worked for UNESCO and would visit Washington D.C., staying with my parents. He would open his suitcase and pull out amazing gadgets — diffraction gratings, holograms — and explain how they worked. I decided physics was the coolest thing there is.

At age eight he gave me his book The New College Physics: A Spiral Approach, which I tried to read immediately. The “spiral approach” is pedagogically valuable: instead of covering a topic once, you revisit it repeatedly, increasing depth each time. He taught me not only physics but also how to learn and teach.

When I was fifteen I spent a couple of weeks at his Berkeley apartment. He showed me the Lawrence Hall of Science, where I got my first taste of programming — in BASIC, with programs stored on paper tape in 1976. He also gave me The Feynman Lectures on Physics. The following summer, while working at a state park building trails, I tried to learn quantum mechanics from the third volume of the lectures. The other kids probably thought I was a complete geek — which I was.

Give us some insight on what your average work day is like

During the school year I teach two or three days a week. On teaching days I prepare classes starting at breakfast. Teaching is lots of fun; right now I’m teaching an undergraduate course on game theory and a graduate course on category theory, and I run a category theory seminar. I also meet with my graduate students for a weekly four-hour session to review progress and push research forward.

On non-teaching days I spend much of my time writing. I love blogging, but I try to devote significant time to writing papers. Early drafts are often tough, but near the end a paper “practically writes itself” and I find it hard to stop adding improvements. Those are very satisfying days.

In summer I don’t teach, so I often get a lot of writing done. I spent two years at the Centre of Quantum Technologies in Singapore, and since 2012 I’ve worked there during summers. Sometimes I bring grad students; mostly I focus on writing.

I also spend plenty of time with my wife — talking, cooking, shopping, working out — and we like to watch TV in the evenings, mainly mysteries and science fiction. We do a lot of gardening. When younger that seemed boring, but as subjective time speeds up with age you notice plants growing: planting seedlings, watching them grow into an orange tree, and eating the fruit for breakfast is tremendously satisfying.

I enjoy playing piano and recording electronic music, but doing these well requires long blocks of time I don’t always have. Music is pure delight; when not listening I’m often composing mentally.

If I gave in to my darkest urges and became a decadent wastrel I might spend all day blogging, listening to music, recording music and working on pure math. But I need other activities to stay sane.

What research are you working on at the moment?

I’ve been trying to finish a paper called “Struggles with the Continuum”, about the problems physics has with infinities arising from treating spacetime as a continuum. Writing sections that summarize quantum field theory is challenging because the subject is complicated and sprawling. To stay motivated I broke the paper into blog articles and posted them on Physics Forums.

For fun, I’ve been collaborating with Greg Egan on projects involving the octonions. The octonions are a number system where you can add, subtract, multiply and divide; such division algebras exist only in dimensions 1, 2, 4 and 8: the real numbers (1D), the complex numbers (2D), the quaternions (4D) and the octonions (8D). The octonions are the largest and the strangest: multiplication of octonions is not associative, so $(xy)z$ need not equal $x(yz)$. Despite sounding crazy at first, octonions connect to string theory and other areas.

The 240 unit integral octonions, projected onto a plane

There is a notion of “integers” for the octonions; integral octonions form a lattice in 8 dimensions called the E₈ lattice. Another important lattice lives in 24 dimensions, the Leech lattice. Both connect to string theory: 8+2 = 10 (superstring dimension) and 24+2 = 26 (bosonic string dimension); the +2 comes from the 2-dimensional worldsheet of the string.

Because 3×8 = 24, Greg Egan and I explored building the Leech lattice from three E₈ copies. There was a known trick; it took time to understand, and then Egan showed the trick can be done in exactly 17,280 ways. I plan to write up the proof; there’s beautiful geometry involved.

My main current work uses category theory to study networks. I’m interested in many network types — electrical circuits, neural networks, chemical reaction networks and more. Different fields focus on different networks, but there is insufficient cross-disciplinary communication, so mathematicians can help build a unified theory of networks.

I have seven graduate students on this project — eight if you include Brendan Fong, whose dissertation I’ve helped advise even though he’s an Oxford student.

Brendan was the first to join. I initially wanted him to study electrical circuits as a familiar starting point, but he developed a general category-theoretic framework for networks. We applied it to electrical circuits and other systems.

Blake Pollard and Brendan Fong at the Centre for Quantum Technologies

Blake Pollard, a student in our physics department, collaborated with Brendan and me to develop a category-theoretic approach to Markov processes, reducing them to electrical circuits. Blake is now extending these ideas to chemical reaction networks.

My math-department students work on related topics. Jason Erbele studies control theory and how “signal flow diagrams” used in engineering can be understood categorically; he has developed categorical descriptions of signal flow. Jason uses a different framework called PROPs, which are longstanding tools in algebraic topology. Franciscus Rebro has developed PROPs further for our project.

Signal flow diagram for an inverted pendulum on a cart

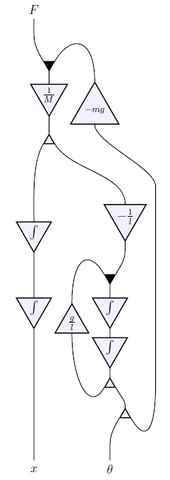
Brandon Coya has worked on electrical circuits, extending Brendan’s work and unifying Brendan’s formalism with PROPs. Adam Yassine is beginning to study networks in classical mechanics: instead of analyzing a single system via a Hamiltonian, he is setting up frameworks to connect many systems into networks.

Kenny Courser and Daniel Cicala are exploring bringing 2-categories into network theory. Categories describe systems and processes that turn inputs into outputs; 2-categories describe meta-processes that turn one process into another. For example, a 2-category can formalize a “simplification” that replaces two resistors in series with a single resistor.

Ultimately I want to apply these ideas to biochemistry. Biology can seem messy to physicists and mathematicians, but I suspect a beautiful logic underlies it. Biological systems are full of networks that change over time, so 2-categories may provide a natural language for them. Convincing others won’t be easy — but that’s okay.

Continue to Part 2 of this interview