Reversible vs Irreversible Gas Compression and Expansion Work
Table of Contents
Introduction
In learning Thermodynamics, one of the difficult concepts that many students struggle with is the difference between reversible and irreversible work in the expansion/compression of a gas. They wonder,
1. Why is it that we need to use two different equations to calculate the work done by the system on the surroundings, one for a reversible process (##dW = PdV##, where P is the gas thermodynamic pressure calculated from the ideal gas law ##P =nRT/V##), and the other for an irreversible process (##dW = P_{ext}dV##, where ##P_{ext}## is the external force per unit area exerted by the surroundings (the piston face) on the gas?
2. Since, by Newton’s third law, the external force per unit area exerted by the surroundings on the gas ##P_{ext}## is equal to the gas thermodynamic pressure at the interface P, shouldn’t the equation ##dW = PdV## for reversible processes also correctly give the work for the irreversible process?
3. What is it fundamentally about irreversible processes that cause the amount of work done by the gas on the surroundings to differ from that for a reversible process?
In the present development, we will address all three of these questions, but our initial focus will be on question 3. Once we explore the answer to this question, the answers to questions 1 & 2 should become more apparent.
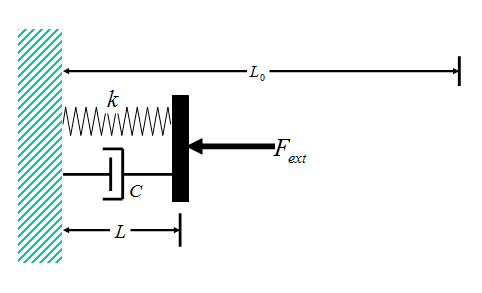
A gas experiencing expansion/compression work behaves in a manner very similar to a spring-damper mechanical system (with the spring and damper connected in parallel, Fig. 1). The spring response is analogous to P-V-T behavior of the gas, in the sense that decreases in length of the spring result in greater compressive force, while decreases in the volume of the gas result in greater pressure. The viscous behavior of the damper is analogous to the viscous response of the gas, in the sense that the force required to compress the damper is proportional to the time rate of length compression of the damper, while the viscous compressive stress in a gas is proportional to the time rate of volumetric compressive strain.
Figure 1 Spring-Damper Model
In the present development, we will begin by analyzing in detail the reversible and irreversible loading of a spring/damper combination and will show that the amount of work required to compress the system in the irreversible case exceeds that in the reversible case by the amount of work required to compress the viscous damper. We shall refer to this as the viscous work. The greater the compressive force ##F_{ext}## and the more rapid the deformation, the larger the amount of viscous work.
We will also note that the total external force required to compress the combined system ##F_{ext}## is not just that required to compress the spring ##F=kΔL##, but also includes a contribution from the viscous damper, and this contribution increases with increasing rate of compression. So we would not expect the applied external force to match that of the spring alone ##F=kΔL## unless the compression is carried out very slowly. This is analogous to the case of irreversible gas compression in which the external force per unit area ##P_{ext}## required to compress the gas is higher than the pressure calculated from the ideal gas law alone ##P =nRT/V##. The force also includes a contribution from the viscous stresses in the gas.
After we have completed our detailed quantitative assessment of the spring-damper system, we will turn attention to the compression/expansion behavior of an ideal gas. While the spring-damper system is sufficiently simple to completely describe its time-dependent behavior for arbitrary transient loading with relative ease, this is not so in the case of an ideal gas. For an ideal gas, the detailed treatment is much more complicated and involves the solution to the complicated gas dynamics equations, including the Navier-Stokes equations, the local thermal energy balance equation (including viscous dissipation), the ideal gas law, and the local continuity/mass-conservation equation. Fortunately, in the special case of a constant external force per unit area ##P_{ext}## applied to the gas, these difficulties can be circumvented, and the total irreversible and reversible work can be determined relatively easily. We will compare these results for an ideal gas with the corresponding findings for a spring-damper system to illustrate quantitatively how closely they resemble one another.
Spring-Damper Model Analysis
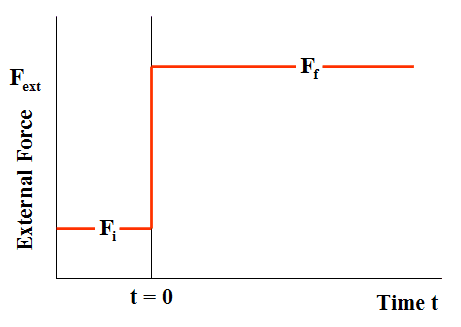
Consider the spring-damper system shown in Fig. 1. The spring and damper are connected in parallel, and the combination is sandwiched between a wall on the left, and a plate on the right. A time-dependent external force ##F_{ext}## is applied to the plate, such that, at all times t < 0, the force ##F_{ext}=F_{i}##, while at all times t > 0, force ##F_{ext}=F_{f}##. The force ##F_{ext}## thus changes discontinuously at time t = 0 (Fig. 2).
Figure 2 External Force Irreversible Loading (Case of compression)
The unextended length of the spring is ##L_0## and, to simulate the behavior of a gas (which can exhibit only compressive force), the spring is assumed to be loaded in compression throughout the entire time-dependent deformation of the system. Thus, the initial equilibrium length of the system ##L_i##, the final equilibrium length ##L_f##, and the length L at time t during the deformation are all less than ##L_0##.
The compressive force exerted by the spring (a) initially, (b) at time t, and (c) in the final equilibrium state of the system are related to the corresponding lengths of the spring by:
$$F_i=k(L_0-L_i)\tag{1-a}$$
$$F=k(L_0-L)\tag{1-b}$$
$$F_f=k(L_0-L_f)\tag{1-c}$$
Unlike the spring element, the compressive force exerted by the viscous damper ##f_V## is related not to the length of the damper L, but rather to the rate of change of the viscous damper length with respect to time:$$f_V=-C\frac{dL}{dt}\tag{2}$$ where C is the so-called “viscous damper constant.”
If we perform a force balance on the (massless) plate in Fig. 1, we obtain $$F+f_V=F_{ext}(t)\tag{3}$$ Note from this equation that the (reversible) spring compressive force is not the only load acting on the plate. There is also the (dissipative) viscous damper force applied to the plate. These two forces combine to determine the overall (constant) force ##F_{ext}## of the spring-damper system.
Substitution of Eqns. 1 and 2 into Eqn. 3 yields (for t > 0):$$k(L_0-L)-C\frac{dL}{dt}=k(L_0-L_f)\tag{4}$$The first term on the left-hand side represents the spring force, the second term represents the viscous damper force, and the right-hand side represents the constant loading force.
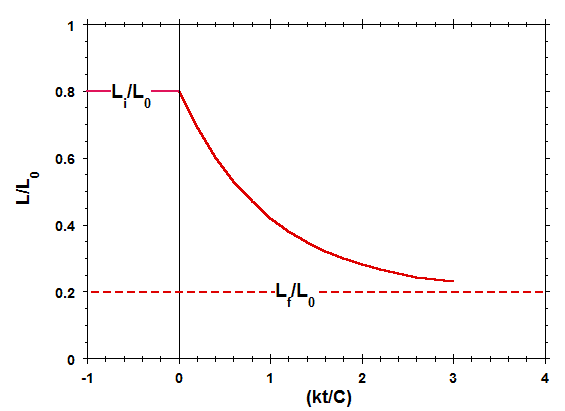
The solution to the this time-dependent differential equation for L, subject to the initial condition ##L=L_i## at t = 0, is given by:$$L=L_f+(L_i-L_f)e^{-(\frac{kt}{C})}\tag{5}$$As determined from Eqn. 5, Fig. 3 shows a plot of the dimensionless length ##L/L_0## as a function of the dimensionless time ##(kt/C)## for the specific case in which ##L_i/L_0=0.8## and ##L_f/L_0=0.2##.
Figure 3 Length of Spring-Damper System vs Time
Comparison of Figs. 2 and 3 indicates that, for the situation currently being considered, while the applied external force ##F_{ext}##changes discontinuously at time t = 0, the length of the spring-damper element L varies continuously (and more gradually) from its initial length to its final length, on a time scale on the order of C/k. This more gradual variation is the direct result of the presence of the viscous damper element in the system. A similar effect occurs when a gas is forced to expand or compress in a cylinder, as a direct result of the viscous behavior of the gas (Yes, even in the low-pressure limit of ideal gas behavior, gases exhibit non-zero viscosity).
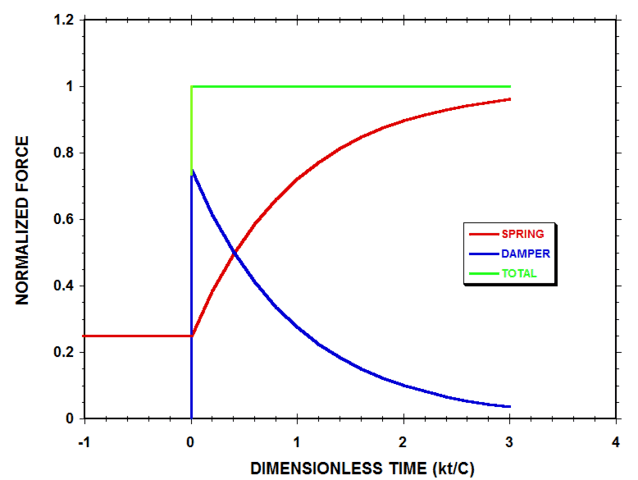
If we substitute Eqn. 5 into Eqns. 1 and 2 for the compressive forces within the system at times t >0, we obtain:$$F=k(L_0-L_f)-k(L_i-L_f)e^{-(\frac{kt}{C})}\tag{6-a}$$$$f_V=k(L_i-L_f)e^{-(\frac{kt}{C})}\tag{6-b}$$$$F_{ext}=k(L_0-L_f)\tag{6-c}$$Eqn. 6-a represents the force exerted by the spring, Eqn. 6-b represents the force exerted by the damper, and Eqn. 6-c represents the total applied compressive force. Fig. 4 shows a plot of these three forces, normalized by ##k(L_0-L_f)##, and plotted as a function of the dimensionless time ##(kt/C)##, for the same compressional case that was considered in Fig. 3.
Figure 4 Normalized Spring-Damper System Forces (with ##L_f=0.2L_0## & ##L_i=0.8L_0##)
According to Fig. 4, the elastic spring continues to support only 25% of the applied load at the instant immediately after the external compressive force ##F_{ext}## is suddenly increased, while the damper, by deforming rapidly and viscously, supports the remaining 75% of the load. As time progresses, the rate of change of damper length with time decreases in magnitude, and the damper supports less of the load, while more of the load is borne by the spring. At the final equilibrium state of the system, the spring supports all the load, and the force of the damper has decayed to zero.
Let us now finally consider the reversible and irreversible work done by the spring-damper system. This can be obtained by multiplying each of Eqns. 6 by the rate of increase of length dL/dt derived from Eqn. 5, and then integrating with respect to time from time t = 0 to t →∞. We thereby obtain:
$$W_R+w_V=W_{Irr}\tag{7}$$
with
$$W_{R}=\int_0^∞F\frac{dL}{dt}dt=\frac{k}{2}\left[(L_0-L_i)^2-(L_0-L_f)^2\right]\tag{8-a}$$
$$w_V=\int_0^∞f_v\frac{dL}{dt}dt=-\frac{k}{2}(L_f-L_i)^2\tag{8-b}$$
$$W_{Irr}=\int_0^∞F_{ext}\frac{dL}{dt}dt=k(L_0-L_f)(L_f-L_i)\tag{8-c}$$
where ##W{_R}## denotes the reversible work, ##w_{v}## denotes the viscous work, and ##W_{Irr}## denotes the irreversible work. Note that the damper constant C no longer appears in these equations, and thus these results for the work done between the initial and final equilibrium states of the system apply irrespective of the (non-zero) value of the damper constant. The reversible work ##W_R## represents that done by the spring alone and is also equal to the change in stored elastic energy of the spring. The irreversible work ##W_{Irr}## represents the combined work done by the spring and damper on their surroundings (the plate) and is determined by the applied external force integrated over its displacement. The viscous work ##w_V## represents the work done by the damper on the surroundings (the plate), and, by virtue of the squared term in Eqn. 8b, is always negative, irrespective of whether the system is being expanded or compressed. Thus, in all situations, the viscous damper robs usable mechanical energy from the surroundings and dissipates it as (less usable) thermal energy.
Fig. 5 shows a plot of the ratio of the irreversible work to the reversible work ##W_{Irr}/W_{R}## as a function of the expansion/compression length ratio ##L_f/L_i## for a typical case in which ##L_f=0.5L_0##.
Figure 5 Ratio of Irreversible Work to Reversible Work vs Length Ratio (Case of ##L_f=0.5L_0##)
Considering work done by the system on the surroundings as positive, in expansion, both ##W_r## and ##W_{Irr}## are positive, while, in compression, both ##W_r## and ##W_{Irr}## are negative. Therefore, as indicated in Fig. 5, the ratio of ##W_{Irr}## to ##W_r## is positive for both expansion and compression. According to the quantitative results presented in Fig. 5, during compression, the irreversible work done by the external force on the system is always greater than the reversible work required to compress the spring, while, during expansion, the irreversible work done on the surroundings by the system is always less than the reversible work done by the spring. The difference between the reversible work and the irreversible work in all these cases is the result of viscous dissipation in the damper element.
In the next section, we will consider the comparison between reversible work and irreversible work for expansion and compression of an ideal gas, and will present a graph analogous to Fig. 5 for this system. The quantitative comparison between these two plots will be very striking.
Ideal Gas Analysis
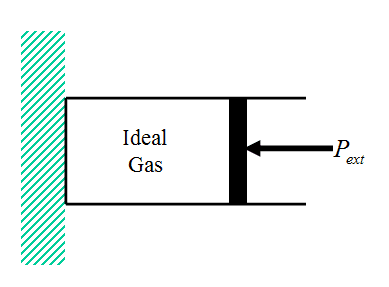
Consider the irreversible expansion or compression of an ideal gas contained in a cylinder featuring a massless frictionless piston (Fig. 6 – compare to Fig. 1). The system is immersed in a constant temperature bath (not shown) at temperature T so that the temperature of the gas in the initial and final equilibrium states of the system is T.
Figure 6 Ideal Gas Cylinder/Piston System
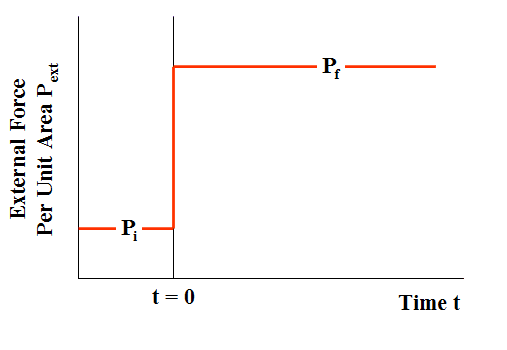
A time-dependent external force per unit area ##P_{ext}## is applied to the piston, such that, at all times t < 0, ##P_{ext}=P_{i}##, while at all times t > 0, ##P_{ext}=P_{f}##. The force per unit area ##P_{ext}## thus changes discontinuously at time t = 0 (Fig. 7, compare with Fig. 2).
Figure 7 External Force Per Unit Area in Irreversible Loading (Case of compression)
The transient physical phenomena occurring within a gas that is irreversibly caused to expand or contract under the action of a sudden change in external force per unit area are substantially more complicated than those occurring in a simple spring-damper system and include
- non-uniform expansion and compression zones traveling back and forth along with the cylinder at speeds on the order of sonic velocities
- large temperature-, pressure-, and density gradients
- local regions of expansion cooling and compressional heating
- non-uniform viscous stresses
- turbulence resulting from the very rapid deformation, causing the gas to behave as if its viscosity were several orders of magnitude higher than the true laminar flow value
Even with all these complexities, the net effect of the change that occurs between the initial and final equilibrium states of the gas system is mechanistically exactly the same as in the case of the spring-damper system: The irreversible work ##W_{Irr}## is equal to the reversible work ##W_{R}## plus the work associated with viscous stresses ##w_{V}## (Eqn. 7).
In the case of the spring-damper system, we calculated the viscous work explicitly by solving for the transient viscous damper force and integrating over the transient displacement (Eqn. 8b). However, we could equally well have obtained the same result simply by subtracting the reversible work from the irreversible work (the equation for each of which is considerably easier to write down). In the case of the ideal gas, we now follow this latter approach. Thus, assuming the irreversible expansion is carried out at constant applied external force per unit area ##P_f=P_{ext}##, the reversible-, irreversible-, and viscous work for isothermal expansion/compression of an ideal gas are given by:
$$W_R=nRT\ln(V_f/V_i)\tag{9a}$$
$$W_{Irr}=P_f(V_f-V_i)=nRT\left(1-V_i/V_f\right)\tag{9b}$$
$$w_V=nRT\left[\left(1-V_i/V_f\right)-\ln(V_f/V_i)\right]\tag{9c}$$
Fig. 8 presents a graph of the viscous work ##w_V##, normalized by nRT, and plotted as a function of the ratio of the final- to the initial volume of the gas ##V_f/V_i## (Eqn. 9c).
Figure 8 Work Done By Viscous Stresses on Piston
The figure indicates that, as in the case of a viscous damper, the work is done on the surroundings (i.e., the piston) by viscous stresses is always negative, irrespective of whether the gas is expanding or being compressed. Thus, as in the case of a viscous damper, the viscous response of the gas always robs usable mechanical energy from the surroundings and dissipates it in the form of (less usable) thermal energy.
Fig. 9 shows a plot of the ratio of the irreversible work to the reversible work ##W_{Irr}/W_{R}## for the case of an ideal gas as a function of the expansion/compression volume ratio ##W_f/W_i##.
Figure 9 Ratio of Reversible Work to Irreversible Work vs Volume Ratio
Considering work done by the system on the surroundings as positive, in expansion, both ##W_r## and ##W_{Irr}## are positive, while, in compression, both ##W_r## and ##W_{Irr}## are negative. Therefore, as indicated in Fig. 9, the ratio of ##W_{Irr}## to ##W_r## is positive for both expansion and compression. This means that, during compression, the irreversible work done by the imposed external force per unit area on the gas is always greater than the reversible work that would have been required to compress the gas, while, during expansion, the irreversible work done against the imposed external force per unit area by the gas is always less than the reversible work that could have been done by the gas.
Finally, note the striking resemblance between Fig. 9 for the case of an ideal gas and Fig. 5 for the corresponding case of a spring-damper system. This comparison provides compelling evidence that the mechanistic cause of the difference between the reversible- and irreversible work in the irreversible expansion/compression of an ideal gas is the rate-dependent viscous work associated with deforming the gas.
Addressing Question 1 and 2 of the Introduction
In a gas cylinder-piston system, the work is done on the surroundings (i.e., on the inner piston face) is always equal to the time-dependent external force per unit area ##P_{ext}## applied at the face, integrated over the volume change. In the special case of a very slow reversible expansion/compression, ##P_{ext}## is also equal to the (uniform) gas thermodynamic pressure within the cylinder, as determined by the ideal gas law (or other real-gas equation of state). However, for a rapid irreversible expansion/compression, the thermodynamic pressure within the cylinder is not spatially uniform, and, moreover, the external force per unit area ##P_{ext}## is not determined solely by the thermodynamic pressure. There is also an additive contribution from the viscous stresses present within the gas at the piston interface. Thus, even if we somehow knew the gas thermodynamic pressure at the piston face, this would still not be sufficient to determine ##P_{ext}##. In an irreversible expansion or compression, the only practical way to obtain a desired ##P_{ext}(t)## is to control it manually from the outside.
Conclusion
A spring-damper system and a gas have a certain key physical characteristic in common: when deformed, they both exhibit viscous behavior which is capable of dissipating mechanical energy and converting it into thermal energy (heat and/or internal energy). The more rapid the deformation, the greater the amount of viscous dissipation. In the present development, we have analyzed the deformation both of a spring-damper system and of gas under expansion/compression loading, and have verified that it is this viscous behavior that is responsible for the difference between the irreversible work and the reversible work done by the system.
PhD Chemical Engineer
Retired after 35 years experience in industry
Physics Forums Mentor









One could consider a baloon submerged in water, increasing the water pressure hydaulically. Like with these bottle imps.
[QUOTE=”Radhakrishnam, post: 5177819, member: 424513″]Introduction of time in the analysis of irreversible process does not pay any dividends, on the other hand there is a possibility that it could be counterproductive, leading to misunderstanding of the simple concepts. [/quote]
I’m beginning to get the feeling that you really don’t like the idea of introducing time into the analysis of irreversible processes:wink:. If you had a valid reason other than the fact that you just plain don’t like it, it might have more impact. The Continuum Mechanics people always use time in their analyses of irreversible processes. Have you been submitting papers in the open literature criticizing them for doing this, with valid arguments for why they must be getting the wrong answers. If so, please share the references. Why single my analysis out as the one you object to most strongly?
[quote]
Let us consider the spring-damper system. Let us take the system through a cycle ABA. Certain amount of net work is done on the system by the external force. As a result, the input work and output work differ, which could be in some form of energy ( such as electrical work, for eg) in the surroundings. The damper exerts a time dependent force. But for that property, there is no indication that the difference in the works for the forward and reverse portions of the cyclic processes, can not be transformed into some energy such as electrical energy. [/quote]
Incorrect. During the irreversible expansion step, the dissipative work done by the piston on the damper is always (a) positive or (b) negative? During the irreverisble compression step, the dissipative work done by the piston on the damper is always (a) positive or (b) negative? So for the cycle, the dissipative work done by the piston on the spring-damper system is always (a) positive or (b) negative?
[quote]
The second point is more important! The pedagogical advantage you see in mechanical analogues to explain irreversible thermodynamic processes could mislead the students, indeed![/quote]
In your opinion.
[quote]
For, it is always possible for us to take a mechanical system through a cycle (whether reversible or irreversible), at the end of which, the system reaches its initial state. However, it is not the case with thermodynamic cyclic processes. For example, it is impossible to take a closed system of ideal gas through an irreversible adiabatic cyclic process! The system, simply will not reach the initial state A by an adiabatic process, after you take it from an equilibrium state A to an equilibrium state B by an irreversible adiabatic process.
[/quote]
Who says I can’t treat the spring-damper system as a thermodynamic system? If I try to take it through an irreversible adiabatic ABA cycle, I will find that, as in the case of an ideal gas, I will not be able to return it to its original state. Dissipative work will have been done in compressing and expanding the damper, and, if the system is adiabatic, its temperature will have risen due to the increase in internal energy of the system. In engineering, we call that “viscous heating.”
So the spring-damper system is fully capable of being treated as a thermodynamic system (and not merely a mechanical system), and, in irreversible expansions and compressions, it exhibits the key characteristics of a gas experiencing the same kind of irreversible process.
Chet
[QUOTE=”DrDu, post: 5178109, member: 210532″]Ok, i never talked about a cylinder with a piston. Consider isotropic stress. Isn’t even for a compressible fluid the hydrodynamic pressure equal to one third of the trace of the stress tensor?[/QUOTE]
If the deformation is isotropic (purely a volume change), then the stress tensor is isotropic, and the stress is the same in all directions. It is equal to the thermdynamic pressure plus a viscous contribution. If you want to call that the hydrodynamic pressure, that’s fine. Even for a non-isotropic deformation, it’s perfectly OK to define the term hydrodynamic pressure as 1/3 the trace of the compressive stress tensor. But, in the expansion or compression of a gas within a cylinder (which is the focus of this thread), the deformation is 1 dimensional (i.e., anisotropic), and the force per unit area exerted on the piston is not equal to the hydrodynamic pressure (as described by this definition).
Chet
Ok, i never talked about a cylinder with a piston. Consider isotropic stress. Isn’t even for a compressible fluid the hydrodynamic pressure equal to one third of the trace of the stress tensor?
[QUOTE=”DrDu, post: 5178085, member: 210532″]So isn’t this in the end the “hhdrodynamic pressure”?[/QUOTE]
In cases where the fluid is deforming and viscous stresses are present, if you are looking at the deformation involved in expansion or compression in a cylinder, the deformation is not isotropic, and the compressive stresses are different in different directions.
For incompressible flow only, the pressure is equal to 1/3 the trace of the compressive stress tensor. But, if the flow is incompressible, 1/3 the trace of the compressive stress tensor includes a volumetric contribution from viscous stresses , and, in gas expansion within a cylinder, because of the anisotropy of the deformation, this will not be equal to the force per unit area on the piston.
Chet
So isn’t this in the end the “hhdrodynamic pressure”?
[QUOTE=”DrDu, post: 5178056, member: 210532″]Ok, but the trace of the stress tensor is usually included in the total pressure.[/QUOTE]
The trace of the stress tensor is equal to 3x the thermodynamic pressure (assuming the sign convention that compressive stresses are positive) plus a contribution from the volumetric viscous deformation (Fluid mechanics is my primary area of expertise). The stress tensor is equal to the thermodynamic pressure times the identity tensor, plus the contributions of the viscous stress components.
Chet
Ok, but the trace of the stress tensor is usually included in the total pressure.
[QUOTE=”DrDu, post: 5177946, member: 210532″]Oh, my fault , I meant that the system pressure of the gas does not vary with position and equals the external pressure.[/QUOTE]
[QUOTE=”DrDu, post: 5177946, member: 210532″]Oh, my fault , I meant that the system pressure of the gas does not vary with position and equals the external pressure.[/QUOTE]
Hi DrDu.
I think you meant here the “system compressive stress” rather than “the system pressure”. The system compressive stress includes the combination of both the thermodynamic pressure [B]and[/B] the viscous stress. This is what is equal to the external pressure.
Chet
Oh, my fault , I meant that the system pressure of the gas does not vary with position and equals the external pressure.
[quote=”DrDu, post: 5176650″][QUOTE=”Radhakrishnam, post: 5176009, member: 424513″]
Whether the process is reversible or irreversible, the equation to calculate work out put is one and the same: Work output =integral(Pext x dV). Work output and work input have opposite signs since dV has opposite signs in the two cases.
For an irreversible process we cannot do that substitution for Pext, and hence, cannot obtain an equation but only an inequation. For expansion process we get lower work output and for a compression process we get more work input compared to that of a reversible process connecting the same end points. We cannot go into an elaboration of this point here in the discussion.
[/QUOTE]
Of course we can write down an equation for Pext also for irreversible processes using irreversible thermodynamics.
Even though irreversible thermodynamics is not in the scope of introductory thermodynamics classes, it seems necessary to give students an idea in what respect non-equilibrium systems differ from equilibrium ones.
In my experience, students have great difficulties to imagine how a difference between equilibrium pressure and pressure away from equilibrium can arise.
My point was to find an easy example where Pext is still spatially constant but not equal to the equilibrium pressure.[/quote]Introduction of time in the analysis of irreversible process does not pay any dividends, on the other hand there is a possibility that it could be counterproductive, leading to misunderstanding of the simple concepts. Let us consider the spring-damper system. Let us take the system through a cycle ABA. Certain amount of net work is done on the system by the external force. As a result, the input work and output work differ, which could be in some form of energy ( such as electrical work, for eg) in the surroundings. The damper exerts a time dependent force. But for that property, there is no indication that the difference in the works for the forward and reverse portions of the cyclic processes, can not be transformed into some energy such as electrical energy. You did mention that the difference in works is dissipated in the form of heat; but it sounds like a request to the students to accept it as an extra fact. Introduction of friction on the other hand would lead to a natural feeling of dissipation into heat. If you still see the spring damper system (that doesn’t have the properties associated with friction, I leave it to you).
The second point is more important! The pedagogical advantage you see in mechanical analogues to explain irreversible thermodynamic processes could mislead the students, indeed!
For, it is always possible for us to take a mechanical system through a cycle (whether reversible or irreversible), at the end of which, the system reaches its initial state. However, it is not the case with thermodynamic cyclic processes. For example, it is impossible to take a closed system of ideal gas through an irreversible adiabatic cyclic process! The system, simply will not reach the initial state A by an adiabatic process, after you take it from an equilibrium state A to an equilibrium state B by an irreversible adiabatic process.
I am yet to see the URL you sent for pressure of time. I will see it at the earliest. People are addicted to Statistical thermodynamics, these days and it is difficult to find people who discuss classical thermodynamics. From this point of view I like your discussion.
Hi Dr Du
Of course we can write down an equation for Pext also for irreversible processes using irreversible thermodynamics.
We can only write equations for the properties such as pressure, temperature etc. of the system, because system is well defined. On the other hand, surroundings is not well defined and doesn’t have unique properties. Having known the pressure of the system, we apply or manipulate the Pext in a way we like. For example for reversible process, we maintain Pext equal to Psys. For irreversible processes Pext is not equal to Psys.
Students should easily be able to imagine that a well defined system at an equilibrium state has a unique value of pressure. A system in a state away from equilibrium doesn’t have a unique values for its properties! Therefore, when a system is away from equilibrium, it is not in a well defined state and as such doesn’t have unique values (or calculable values) for its properties.
I am unable to appreciate your statement: ‘My point was to find an easy example where Pext is still spatially constant but not equal to the equilibrium pressure.’
What is the meaning of spatially constant ( but not equal to the equilibrium pressure), Pext?
P. Radhakrishnamurty
[QUOTE=”Radhakrishnam, post: 5177799, member: 424513″]
The second point is more important! The pedagogical advantage you see in mechanical analogues to explain irreversible thermodynamic processes could mislead the students, indeed!
[/QUOTE]
I did never claim any pedagogical advantage in mechanical analogues!
[quote=”DrDu, post: 5176650″][QUOTE=”Radhakrishnam, post: 5176009, member: 424513″]
Whether the process is reversible or irreversible, the equation to calculate work out put is one and the same: Work output =integral(Pext x dV). Work output and work input have opposite signs since dV has opposite signs in the two cases.
For an irreversible process we cannot do that substitution for Pext, and hence, cannot obtain an equation but only an inequation. For expansion process we get lower work output and for a compression process we get more work input compared to that of a reversible process connecting the same end points. We cannot go into an elaboration of this point here in the discussion.
[/QUOTE]
Of course we can write down an equation for Pext also for irreversible processes using irreversible thermodynamics.
Even though irreversible thermodynamics is not in the scope of introductory thermodynamics classes, it seems necessary to give students an idea in what respect non-equilibrium systems differ from equilibrium ones.
In my experience, students have great difficulties to imagine how a difference between equilibrium pressure and pressure away from equilibrium can arise.
My point was to find an easy example where Pext is still spatially constant but not equal to the equilibrium pressure.[/quote]Introduction of time in the analysis of irreversible process does not pay any dividends, on the other hand there is a possibility that it could be counterproductive, leading to misunderstanding of the simple concepts. Let us consider the spring-damper system. Let us take the system through a cycle ABA. Certain amount of net work is done on the system by the external force. As a result, the input work and output work differ, which could be in some form of energy ( such as electrical work, for eg) in the surroundings. The damper exerts a time dependent force. But for that property, there is no indication that the difference in the works for the forward and reverse portions of the cyclic processes, can not be transformed into some energy such as electrical energy. You did mention that the difference in works is dissipated in the form of heat; but it sounds like a request to the students to accept it as an extra fact. Introduction of friction on the other hand would lead to a natural feeling of dissipation into heat. If you still see the spring damper system (that doesn’t have the properties associated with friction, I leave it to you).
The second point is more important! The pedagogical advantage you see in mechanical analogues to explain irreversible thermodynamic processes could mislead the students, indeed!
For, it is always possible for us to take a mechanical system through a cycle (whether reversible or irreversible), at the end of which, the system reaches its initial state. However, it is not the case with thermodynamic cyclic processes. For example, it is impossible to take a closed system of ideal gas through an irreversible adiabatic cyclic process! The system, simply will not reach the initial state A by an adiabatic process, after you take it from an equilibrium state A to an equilibrium state B by an irreversible adiabatic process.
I am yet to see the URL you sent for pressure of time. I will see it at the earliest. People are addicted to Statistical thermodynamics, these days and it is difficult to find people who discuss classical thermodynamics. From this point of view I like your discussion.
[QUOTE=”DrDu, post: 5176650, member: 210532″]Of course we can write down an equation for Pext also for irreversible processes using irreversible thermodynamics.
Even though irreversible thermodynamics is not in the scope of introductory thermodynamics classes, it seems necessary to give students an idea in what respect non-equilibrium systems differ from equilibrium ones.
In my experience, students have great difficulties to imagine how a difference between equilibrium pressure and pressure away from equilibrium can arise.
My point was to find an easy example where Pext is still spatially constant but not equal to the equilibrium pressure.[/QUOTE]
Hi Dr. Du. Thank you for your perceptive comment.
I’d like to elaborate a little on your response. It is not usually necessary to use irreversible thermodynamics to solve problems with irreversible gas dynamics, and to take into account the fact that the compressive stress which each parcel of gas exerts on its neighbors (as well as on solid boundaries) is not equal to the thermodynamic pressure (determined by the local temperature and density). Computational Fluid Dynamics (CFD) can adequately handle quantification of these effects, even if the deformation is turbulent. In both our comments within this thread, we correctly noted that, during an irreversible deformation, the difference between the compressive stresses within a gas and the thermodynamic pressure is attributable to the viscous stresses, which depend on the rate of deformation. I strongly agree with you that “it seems necessary to give students an idea in what respect non-equilibrium systems differ from equilibrium ones,” and this answers that question (at least for mechanical irreversibilities).
In my judgement, the assumption that the compressive stress within the deforming gas is nearly uniform and equal to the externally applied force per unit area at the boundary, P[SUB]ext[/SUB], is usually a good one. This is because compression waves travel through a gas at the speed of sound, and the time scale for the expansion or compression is typically much larger than the time scale for a wave to travel across the system. However, of course, there can be situations in practice where this is not the case, such as in internal combustion engines.
Irrespective of whether the compressive stress within the system is uniform or not, the parameter P[SUB]ext[/SUB] is usually used to refer to the external force per unit area applied at the boundary (interface) between the system and the surroundings. In his comment, Radhakrishnam seems to imply with regard to P[SUB]ext[/SUB] that, if the process is irreversible, then all bets are off and P[SUB]ext[/SUB] can not be established. However, this is not the case. We are perfectly free to impose any external force loading history that we choose at the boundary of our system. In many cases, once this loading history is established, the system can be solved deterministically for the final equilibrium state. This is certainly the case for a constant external force per unit area imposed in an irreversible expansion or compression within a cylinder.
Chet
[QUOTE=”Radhakrishnam, post: 5176009, member: 424513″]Time has no role to play in thermodynamics (Classical or Equilibrium).[/QUOTE]
Steam takes a finite time to transition from one condition of dryness/wetness to another during an expansion .
Otherwise identical expansions should give slightly different work outputs and have slightly different end conditions depending on rate of expansion ?
[QUOTE=”Radhakrishnam, post: 5176009, member: 424513″]
Whether the process is reversible or irreversible, the equation to calculate work out put is one and the same: Work output =integral(Pext x dV). Work output and work input have opposite signs since dV has opposite signs in the two cases.
For an irreversible process we cannot do that substitution for Pext, and hence, cannot obtain an equation but only an inequation. For expansion process we get lower work output and for a compression process we get more work input compared to that of a reversible process connecting the same end points. We cannot go into an elaboration of this point here in the discussion.
[/QUOTE]
Of course we can write down an equation for Pext also for irreversible processes using irreversible thermodynamics.
Even though irreversible thermodynamics is not in the scope of introductory thermodynamics classes, it seems necessary to give students an idea in what respect non-equilibrium systems differ from equilibrium ones.
In my experience, students have great difficulties to imagine how a difference between equilibrium pressure and pressure away from equilibrium can arise.
My point was to find an easy example where Pext is still spatially constant but not equal to the equilibrium pressure.
[QUOTE=”Radhakrishnam, post: 5176009, member: 424513″]The concept of reversibility in thermodynamics is very important. The difficulty students face in understanding the concept is also genuine, especially in view of the fact that there exist many a way in which the concept is sought to be explained to them in simple and more simple ways. Unfortunately, not all of them are equivalent or reinforce one another.
The easiest way the correct concept of reversible process can be obtained is from the definition given by Max Planck, in his Treatise on Thermodynamics, which says, ‘A process is said to be irreversible, if it is impossible with the assistance of all agents in nature, to bring the system back to its original state without leaving any changes elsewhere in the universe, once the process has occurred.’ A process which is not irreversible is reversible.
In view of this definition, it would be always useful to conceive of a cyclic process that consists of the process of interest as a part of the cycle and then see if there are any changes left in the surroundings at the end of the cycle, that it is impossible to bring the surroundings back to its original state.
With this brief background, let us see the difference in the work output (or work input) of a reversible and irreversible process connecting two equilibrium states i and f of a closed system of a given mass of ideal gas.
During the course of a reversible process, the system is in a state of equilibrium (within as well as with the surroundings) at any point of the process along the path i-f. That is, properties of the system have unique values for any state j on the path i-f. In contrast to this, for an irreversible process connecting the states i and f, the system will not be at equilibrium and will not have unique values for its properties at any intermediate point along the irreversible path i-f.
Since the system is in equilibrium with surroundings at any point j along the reversible path i-f, the values of the intensive properties of the system, such as temperature, pressure are equal to the values of the corresponding external variables. Therefore, for a reversible process of expansion (or compression) of an ideal gas, Pext = Pgas, Work output =integral(Pext x dV). For an irreversible process, Pext is not equal to Pgas.
Whether the process is reversible or irreversible, the equation to calculate work out put is one and the same: Work output =integral(Pext x dV). Work output and work input have opposite signs since dV has opposite signs in the two cases.
For an irreversible process we cannot do that substitution for Pext, and hence, cannot obtain an equation but only an inequation. For expansion process we get lower work output and for a compression process we get more work input compared to that of a reversible process connecting the same end points. We cannot go into an elaboration of this point here in the discussion.
[/quote]
I completely agree with everything you have said up to here. In fact, the very points you have emphasized, for the most part, are covered in my earlier Insights article at the following link: [URL]https://www.physicsforums.com/insights/understanding-entropy-2nd-law-thermodynamics/[/URL]. I would be pleased to receive feedback from you on that article as well.
[quote]
Bringing ‘time’ to play For reversible processes, we can substitute the known value of Pgas for Pext and get: Wr = nRTln(Vf/Vi).
a role in explanation of thermodynamic process deprives thermodynamics of its vital strengths. Time has no role to play in thermodynamics (Classical or Equilibrium).
While mechanical processes are covered by laws of thermodynamics, thermodynamics is more general and covers the processes that involve heat which is not a part of mechanics. All mechanical processes, in principle, are reversible. Therefore, there is no scope to introduce irreversible processes through mechanical analogs.
[/QUOTE]
These last two paragraphs are where we differ in our perspectives. Regarding the first paragraph, certainly time is not very important in discussing reversible processes. However, for irreversible processes, the speed at which a deformation occurs determines the rate at which mechanical energy is dissipated into thermal energy, and certainly, time is relevant to that. In any event, unlike you, I see no compelling reason why time should be excluded from the discussion of irreversible processes.
With respect to the second paragraph, I disagree with the contention that mechanical processes, in principle, are reversible. Any mechanical process that involves frictional dissipation or viscous dissipation of mechanical energy to thermal energy cannot be regarded as inherently reversible. Certainly processes like these cannot be considered reversible within the context of the definition you attributed to Max Planck (and which I fully agree with). So, whereas you feel that there is no value in introducing irreversible processes through mechanical analogs (at least mechanically irreversible processes), my judgement is that there is great pedagogical value in doing this. I guess we are just going to have to disagree on this.
Chet
[QUOTE=”DrDu, post: 5136875, member: 210532″]Thank’s Chet.
What is also a pedagogical point is the fact that many students conclude from the equilibrium states of a gas being describable in terms of, say, p and T, that there can only be p-V work being done on a gas.
As your analysis already showed, there are many more possibilities. A specifically simple example would be stirring.
If one really wants to consider only p-V work, I think the model with bulk viscosity is one of the simplest. It has the additional bonus that the viscosity can be understood relatively easily, especially if you are a chemical enigneer to be.[/quote]
In the equation I wrote, the viscosity parameter κ also includes the extensional viscosity of the gas which, for the kinematics of this deformation, is equal to twice the shear viscosity.
[quote]
The main effect behind bulk viscosity is the non-equilibrium distribution of the distances of the particles of the gas. This can be shown for e.g. a van der Waals gas, but, even more intuitively for gases whose non-ideal behaviour is due to chemical reactions.
E.g. Nitrogen dioxide is partially dimerized at room temperature and the degree of dimerization depends on pressure and temperature : 2 NO2 <--> N2O4
If the system is compressed rapidly, than there will be more NO2 than what would correspond to equilibrium and the pressure would be higher than the equilibrium pressure. At expansion, there would be more N2O4 and the pressure correspondingly lower. Given we reaction constants of this reaction, we could even calculate the coefficient of viscosity from this.[/QUOTE]
I don’t quite follow what you are saying here. It appears you are talking about an adiabatic expansion/compression, but are you referring to the situation when the final equilibrium state is reached or to the situation immediately after the volume change is complete, but before the system has reached final thermodynamic equilibrium?
Chet
[QUOTE=”DrDu, post: 5135863, member: 210532″]I also find it helpful to consider the example of the compression of a gas when the gas is viscuous and remains homogeneous. This is approximately the case in sound waves and is the main mechanism for the damping of sound waves in gases.
There, one distiguishes between the mechanical pressure ##p_m## and the usual thermodynamical pressure ##p_t##. The two are related as ##p_m=p_t +kappa frac{1}{rho} frac{drho}{dt}##, where ##kappa## is the coefficient of bulk viscosity and ##rho## is the density. While the mechanical pressure is constant and equal to the external pressure, the thermodynamic pressure is smaller. It is clear that the friction represents a source of entropy. It can also be seen that the extra work done ## -kappa frac{1}{rho}frac{drho}{dt}dV ## vanishes when the process is done quasi-statically.[/QUOTE]
Hi DrDu,
Great minds must think alike. I had originally planned to do exactly what you describe, and had even worked out the solution for the volume as a function of time, but, in the end, I decided to leave the analysis out of the article. My starting equation was essentially the same as yours:
$$frac{nRT}{V_f}=frac{nRT}{V}-{kappa}frac{1}{V}frac{dV}{dt}$$
One reason for omitting the analysis was that I determined that, for typical values of the parameters (including the viscosity) in the irreversible case, the velocity of the piston would exceed the speed of sound in the gas at time zero. This is because the distributed mass of the gas is omitted from the model, and also because turbulence, which would increase the effective value of gas viscosity, is also omitted. I just didn’t want to have to deal these points in detail in the article. However, as you say, if I had continued the analysis to the end anyway, I would have obtained the same final result for the viscous work as in the article.
Thanks for bringing this up. It’s a great point.
Chet
Good job, Chet. I wish I was far enough along in my schooling to understand it though. :wink:
Introduction of time in the analysis of irreversible process does not pay any dividends, on the other hand there is a possibility that it could be counterproductive, leading to misunderstanding of the simple concepts. Let us consider the spring-damper system. Let us take the system through a cycle ABA. Certain amount of net work is done on the system by the external force. As a result, the input work and output work differ, which could be in some form of energy ( such as electrical work, for eg) in the surroundings. The damper exerts a time dependent force. But for that property, there is no indication that the difference in the works for the forward and reverse portions of the cyclic processes, can not be transformed into some energy such as electrical energy. You did mention that the difference in works is dissipated in the form of heat; but it sounds like a request to the students to accept it as an extra fact. Introduction of friction on the other hand would lead to a natural feeling of dissipation into heat. If you still see the spring damper system (that doesn't have the properties associated with friction, I leave it to you).The second point is more important! The pedagogical advantage you see in mechanical analogues to explain irreversible thermodynamic processes could mislead the students, indeed! For, it is always possible for us to take a mechanical system through a cycle (whether reversible or irreversible), at the end of which, the system reaches its initial state. However, it is not the case with thermodynamic cyclic processes. For example, it is impossible to take a closed system of ideal gas through an irreversible adiabatic cyclic process! The system, simply will not reach the initial state A by an adiabatic process, after you take it from an equilibrium state A to an equilibrium state B by an irreversible adiabatic process.I am yet to see the URL you sent for pressure of time. I will see it at the earliest. People are addicted to Statistical thermodynamics, these days and it is difficult to find people who discuss classical thermodynamics. From this point of view I like your discussion.Hi Dr DuOf course we can write down an equation for Pext also for irreversible processes using irreversible thermodynamics. We can only write equations for the properties such as pressure, temperature etc. of the system, because system is well defined. On the other hand, surroundings is not well defined and doesn't have unique properties. Having known the pressure of the system, we apply or manipulate the Pext in a way we like. For example for reversible process, we maintain Pext equal to Psys. For irreversible processes Pext is not equal to Psys. Students should easily be able to imagine that a well defined system at an equilibrium state has a unique value of pressure. A system in a state away from equilibrium doesn't have a unique values for its properties! Therefore, when a system is away from equilibrium, it is not in a well defined state and as such doesn't have unique values (or calculable values) for its properties.I am unable to appreciate your statement: 'My point was to find an easy example where Pext is still spatially constant but not equal to the equilibrium pressure.'What is the meaning of spatially constant ( but not equal to the equilibrium pressure), Pext?P. Radhakrishnamurty
Introduction of time in the analysis of irreversible process does not pay any dividends, on the other hand there is a possibility that it could be counterproductive, leading to misunderstanding of the simple concepts. Let us consider the spring-damper system. Let us take the system through a cycle ABA. Certain amount of net work is done on the system by the external force. As a result, the input work and output work differ, which could be in some form of energy ( such as electrical work, for eg) in the surroundings. The damper exerts a time dependent force. But for that property, there is no indication that the difference in the works for the forward and reverse portions of the cyclic processes, can not be transformed into some energy such as electrical energy. You did mention that the difference in works is dissipated in the form of heat; but it sounds like a request to the students to accept it as an extra fact. Introduction of friction on the other hand would lead to a natural feeling of dissipation into heat. If you still see the spring damper system (that doesn't have the properties associated with friction, I leave it to you).The second point is more important! The pedagogical advantage you see in mechanical analogues to explain irreversible thermodynamic processes could mislead the students, indeed! For, it is always possible for us to take a mechanical system through a cycle (whether reversible or irreversible), at the end of which, the system reaches its initial state. However, it is not the case with thermodynamic cyclic processes. For example, it is impossible to take a closed system of ideal gas through an irreversible adiabatic cyclic process! The system, simply will not reach the initial state A by an adiabatic process, after you take it from an equilibrium state A to an equilibrium state B by an irreversible adiabatic process.I am yet to see the URL you sent for pressure of time. I will see it at the earliest. People are addicted to Statistical thermodynamics, these days and it is difficult to find people who discuss classical thermodynamics. From this point of view I like your discussion.
The concept of reversibility in thermodynamics is very important. The difficulty students face in understanding the concept is also genuine, especially in view of the fact that there exist many a way in which the concept is sought to be explained to them in simple and more simple ways. Unfortunately, not all of them are equivalent or reinforce one another. The easiest way the correct concept of reversible process can be obtained is from the definition given by Max Planck, in his Treatise on Thermodynamics, which says, 'A process is said to be irreversible, if it is impossible with the assistance of all agents in nature, to bring the system back to its original state without leaving any changes elsewhere in the universe, once the process has occurred.' A process which is not irreversible is reversible.In view of this definition, it would be always useful to conceive of a cyclic process that consists of the process of interest as a part of the cycle and then see if there are any changes left in the surroundings at the end of the cycle, that it is impossible to bring the surroundings back to its original state.With this brief background, let us see the difference in the work output (or work input) of a reversible and irreversible process connecting two equilibrium states i and f of a closed system of a given mass of ideal gas. During the course of a reversible process, the system is in a state of equilibrium (within as well as with the surroundings) at any point of the process along the path i-f. That is, properties of the system have unique values for any state j on the path i-f. In contrast to this, for an irreversible process connecting the states i and f, the system will not be at equilibrium and will not have unique values for its properties at any intermediate point along the irreversible path i-f.Since the system is in equilibrium with surroundings at any point j along the reversible path i-f, the values of the intensive properties of the system, such as temperature, pressure are equal to the values of the corresponding external variables. Therefore, for a reversible process of expansion (or compression) of an ideal gas, Pext = Pgas, Work output =integral(Pext x dV). For an irreversible process, Pext is not equal to Pgas. Whether the process is reversible or irreversible, the equation to calculate work out put is one and the same: Work output =integral(Pext x dV). Work output and work input have opposite signs since dV has opposite signs in the two cases.For an irreversible process we cannot do that substitution for Pext, and hence, cannot obtain an equation but only an inequation. For expansion process we get lower work output and for a compression process we get more work input compared to that of a reversible process connecting the same end points. We cannot go into an elaboration of this point here in the discussion.Bringing 'time' to play For reversible processes, we can substitute the known value of Pgas for Pext and get: Wr = nRTln(Vf/Vi).a role in explanation of thermodynamic process deprives thermodynamics of its vital strengths. Time has no role to play in thermodynamics (Classical or Equilibrium).While mechanical processes are covered by laws of thermodynamics, thermodynamics is more general and covers the processes that involve heat which is not a part of mechanics. All mechanical processes, in principle, are reversible. Therefore, there is no scope to introduce irreversible processes through mechanical analogs.Radhakrishnamurty P,
Thank's Chet. What is also a pedagogical point is the fact that many students conclude from the equilibrium states of a gas being describable in terms of, say, p and T, that there can only be p-V work being done on a gas. As your analysis already showed, there are many more possibilities. A specifically simple example would be stirring. If one really wants to consider only p-V work, I think the model with bulk viscosity is one of the simplest. It has the additional bonus that the viscosity can be understood relatively easily, especially if you are a chemical enigneer to be. The main effect behind bulk viscosity is the non-equilibrium distribution of the distances of the particles of the gas. This can be shown for e.g. a van der Waals gas, but, even more intuitively for gases whose non-ideal behaviour is due to chemical reactions. E.g. Nitrogen dioxide is partially dimerized at room temperature and the degree of dimerization depends on pressure and temperature : 2 NO2 <–> N2O4If the system is compressed rapidly, than there will be more NO2 than what would correspond to equilibrium and the pressure would be higher than the equilibrium pressure. At expansion, there would be more N2O4 and the pressure correspondingly lower. Given we reaction constants of this reaction, we could even calculate the coefficient of viscosity from this.
I also find it helpful to consider the example of the compression of a gas when the gas is viscuous and remains homogeneous. This is approximately the case in sound waves and is the main mechanism for the damping of sound waves in gases. There, one distiguishes between the mechanical pressure ##p_m## and the usual thermodynamical pressure ##p_t##. The two are related as ##p_m=p_t +\kappa \frac{1}{\rho} \frac{d\rho}{dt}##, where ##\kappa## is the coefficient of bulk viscosity and ##\rho## is the density. While the mechanical pressure is constant and equal to the external pressure, the thermodynamic pressure is smaller. It is clear that the friction represents a source of entropy. It can also be seen that the extra work done ## -\kappa \frac{1}{\rho}\frac{d\rho}{dt}dV ## vanishes when the process is done quasi-statically.
Another masterpiece from @chestermiller!