Mass Inflation Inside Black Holes — Explanation & Equations

Definition and summary

Abstract from Poisson and Israel (1990), “Internal structure of black holes”:

“The gravitational effects associated with the radiative tail produced by a gravitational collapse with rotation are investigated. It is shown that the infinite blueshift of the tail’s energy density occurring at the Cauchy horizon of the resulting black hole causes classically unbounded inflation of the effective internal gravitational-mass parameter of the hole. Since this effect is causally disconnected from any external observer, the black-hole external mass remains bounded. The mass inflation phenomenon causes the spacetime curvature to grow to Planckian scales on a spacelike hypersurface in the vicinity of the Cauchy horizon, beyond which the classical laws of general relativity break down. A consequence is that an observer’s trip to this hypersurface embraces all but the last Planck time of the entire black-hole classical history.”

From “Structure of the Inner Singularity of a Spherical Black Hole” (co-written with W. Israel, 1994):

“(Poisson’s) doctoral dissertation was on the concept of mass inflation (not to be confused with cosmological inflation), which he pioneered with Israel in a series of seminal papers. Prior to the understanding of mass inflation, it was believed that wormholes into other universes would be found inside some black holes. Mass inflation closes off these wormholes in realistic black holes. Poisson’s work on black hole interiors has been reviewed in popular science books as well as in the scientific press.”

Key equations

The inner mass parameter m₂(v) diverges at the Cauchy horizon, producing a curvature singularity. The behaviour can be summarized (using the notation from the cited papers) as:

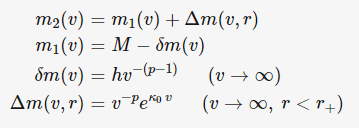
Here:

• Δm is the mass-energy of the outgoing null shell S.
• M is the external gravitational mass (gravitational radius).
• δm is the mass-energy of the late-time radiation influx (Price tails).
• h is a constant related to the gravitational source.
• v is the ingoing null coordinate.
• p determines the decay rate of the ingoing radiation (for gravitational radiation typically p ≥ 11).
• κ is the Cauchy-horizon Killing surface gravity.

Because δm decays with an inverse power law (Price’s law) but the shell contribution Δm grows exponentially near the Cauchy horizon, the total inner mass parameter diverges as the shell approaches the Cauchy horizon.

Cauchy-horizon Killing surface gravity

The Killing-surface gravity at the Cauchy horizon is

κ₀ = (r₊ − r₋) / [2 (r₋² + a²)]

where r₊ is the outer (event) horizon, r₋ is the inner (Cauchy) horizon, and a is the spin parameter (in geometric units).

The inner mass parameter can be written as

m₂(v) = M − h v^{-(p−1)} + v^{−p} e^{κ₀ v}

Inside the event horizon the exponential term dominates as v → ∞, so Δm diverges and m₂(v) grows without bound near the Cauchy horizon. Outside the event horizon (r > r₊), the mass stays bounded and at late times resembles an outer mass function m₁(v).

Extended explanation

Null coordinates and the tortoise coordinate

In Eddington–Finkelstein (or related) coordinates the null coordinates are

v = t + r* (ingoing), and u = t − r* (outgoing), where r* is the tortoise coordinate.

The tortoise coordinate encodes how coordinate time stretches near the horizon: geodesics take an infinite coordinate time to reach the horizon as seen from infinity. For flat (Minkowski) space, v = t + r ≡ 2r, but for curved spacetime v = t + r* ≠ 2r. The relations r* = (v − u) / 2 and t = (v + u) / 2 hold.

Tortoise coordinate for rotating (Kerr) black holes

For Kerr spacetime the radial differential is

dr* = (r² + a²) / Δ · dr, where Δ = r² − 2 M r + a² = (r − r₊)(r − r₋).

An explicit form is

r*(r) = r + [2 M r₊ / (r₊ − r₋)] ln |(r − r₊) / (2 M)| − [2 M r₋ / (r₊ − r₋)] ln |(r − r₋) / (2 M)|.

This reduces to the static (Schwarzschild) form when a = 0. Typical coordinate limits: with v = t + r*, v → ∞ at large radii, v → −∞ at r = r₊, v → ∞ at r = r₋, and v is finite at r = 0 (the opposite signs apply for u).

For Kerr–Newman (charged and rotating) the same transformations apply with Δ = r² − 2 M r + a² + Q² and r₊, r₋ = M ± sqrt(M² − a² − Q²).

Potential barrier and scattering

Perturbations are scattered by the black hole’s external potential barrier. Part of the late-time radiation (Price tails) is backscattered into the hole and contributes to the ingoing flux δm. There are effective “peaks” or potential barriers (often referenced as the peak at r₀ or as related to v = 0), where scattering concentrates.

Inside the event horizon the radiation that crosses the horizon is scattered again by an inner gravitational potential barrier; these multiple scatterings feed the ingoing tail that drives mass inflation near the Cauchy horizon.

References discussing these scattering/peak features include arXiv:gr-qc/9411050 and arXiv:gr-qc/9805008 (see notes and figures in those papers).

Invariant curvature scalar (Kretschmann scalar)

Mass inflation replaces the external mass parameter M by the divergent inner mass parameter m₂(v) in curvature invariants. For Kerr spacetime a form of the Kretschmann scalar incorporating m₂(v) is

K = R_{abcd} R^{abcd} = 48 m₂(v)² (r² − a² cos²θ) [(r² + a² cos²θ)² − 16 r² a² cos²θ] / (r² + a² cos²θ)⁶

where a = J / (m c) (in geometric units often written simply as a = J / m) and θ is the polar angle. Replacing M with m₂(v) produces a curvature invariant that blows up at the Cauchy horizon. In Kerr geometry there are two relevant singular loci: one associated with the inner horizon r = r₋, and the ring singularity at r = 0, θ = π/2.

Sources and further reading

• “The Universality of Mass Inflation Inside Black Holes” — J. S. F. Chan; see related summary: Black Holes Really Exist.
• “Structure of the Inner Singularity of a Spherical Black Hole” — A. Bonanno, S. Droz, W. Israel, S. M. Morsink: arXiv:gr-qc/9403019.
• “Mass Inflation in a Rotating Charged Black Hole” — A. Bonanno: arXiv:gr-qc/9507047.
• Poisson & Israel (1990), “Internal structure of black holes” (see text and references).

Additional links:

• http://uwspace.uwaterloo.ca/handle/10012/225
• http://arxiv.org/abs/gr-qc/9411050
• Comments and discussion: Physics Forums thread
• Related basics: Learn thermodynamics basics