Ambiguous SSA Case in Triangles — Law of Sines Explained

What is the ambiguous case?

In U.S. high schools, students are often introduced to geometric proofs for the first time. A common task is to use a small set of rules to show two triangles are congruent — that is, they have the same side lengths and the same angles. Acronyms such as SAS (side-angle-side) and AAS (angle-angle-side) may sound familiar.

This topic is polarizing: it quickly separates “I love geometry!” students from those who think “I miss algebra!” All of these acronyms simply describe the information given about a triangle. The order of that information matters. For instance, SAS and SSA both involve one angle and two sides, but SSA is not generally sufficient to prove triangles congruent.

Side–Side–Angle (SSA) Triangles

One problematic case is side–side–angle (SSA), sometimes jokingly called “angle–side–side.” When you are given SSA information, this is known as the ambiguous case because it can produce 0, 1, or 2 distinct triangles. Many teachers correctly note SSA does not guarantee congruence; here we explore the reason SSA can produce no triangle at all.

How to analyze an SSA (ambiguous) case

Procedure

1. Draw the triangle and label all given information. It does not need to be to scale. Make sure each side is opposite its corresponding angle: side a opposite angle A, side b opposite angle B, and side c opposite angle C.
2. Use the Law of Sines to try to find the unknown angle opposite the unpaired side. In an SSA setup you have two sides and one non-included angle; apply the Law of Sines to the known angle/side pair to attempt to solve for the angle opposite the second given side.

SSA triangle example

Let’s work through an example. (Note on labeling: the calculation below treats the given acute angle as the one paired with side a. To align the algebra with the displayed calculation we will read the given 55° as the angle paired with side a.)

Given values

Given: $$B = 55 ^{circ}, b=8.99,a=26.22$$

Drawings

Draw the triangle and label the known values.

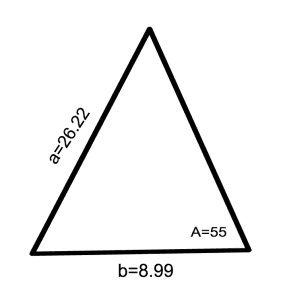
Angle A is shown in the lower-right in this drawing. You could place angle A at the top instead — the orientation does not affect the analysis.

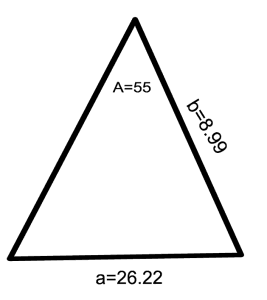
Applying the Law of Sines

The Law of Sines states: $$displaystyle frac{sin(A)}{a}=frac{sin(B)}{b}=frac{sin(C)}{c}$$

As described above, use the Law of Sines to solve for the unknown angle opposite the second given side. The worked computation follows:

$$begin{align*} frac{sin(55^{circ})}{26.22}&=frac{sin(B)}{8.99} \ sin(B) &= frac{26.22sin(55^{circ})}{8.99} \ sin(B) &approx 2.389 end{align*}$$

Why no triangle exists

We have a problem. The sine function has range [-1, 1], so an output of approximately 2.389 is impossible. There is no angle B that satisfies this equation, so no triangle exists for these given values.

Try entering sin^{-1}(2.389) into a calculator and you will get an error — another way to see there is no solution.

Key points

• Always draw and label the triangle first. It does not need to be to scale.
• Apply the Law of Sines to the known angle–side pair and attempt to solve for the angle opposite the other given side.
• If you compute sin(A), sin(B), or sin(C) and the result lies outside the interval [-1, 1], then no triangle exists for the given SSA data.
• If the result falls inside [-1, 1], you must then determine whether there is one or two possible triangle solutions (the classic ambiguous outcome).