Mathematics Articles

Mathematics as the study of “relationships” rather than “patterns” but they are obviously closely related(!). There is a field of mathematics called “category theory” that is just about as abstract as you can get (the textbook, in the preface, said category theory is often called “abstract nonsense” with no sense of that being derogatory at all).

A category has “objects” and “relations”. The collection of all sets is a category with sets as objects and functions between them as “relations”. The collection of topological spaces is a category with the topological spaces being the objects and continuous functions from one topological space to another being the relations.

Tag Archive for: mathematics

vector spaces

Vector Spaces: Concepts, History, and Applications Guide

/
1 Comment
The Concept A vector space is an additively written abelian group together with a field that operates on it.Intuitive picture vs abstract definition Vector…
complex numbers views

Views On Complex Numbers

/
70 Comments
Abstract Why do we need yet another article about complex numbers? This is a valid question and I have asked it myself. I could mention that I wanted…
Lambert W Function in Finance

The Lambert W Function in Finance

/
0 Comments
Preamble The classical mathematician practically by instinct views the continuous process as the "real" process, and the discrete process as an approximation…
infinity

Why Division by Zero Is Impossible: 10 Mathematical Reasons

/
33 Comments
A division by zero is primarily an algebraic question. The reasoning therefore follows the indirect pattern of most algebraic proofs:What if it was…
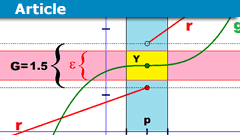
Epsilontic limits and continuity

Epsilontic – Limits and Continuity

/
1 Comment
Abstract I remember that I had some difficulties moving from school mathematics to university mathematics. From what I read on PF through the years, I…
Differential Equation Systems and Nature

Differential Equation Systems and Nature

/
12 Comments
Abstract "Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…
calc precalc

Beginners Guide to Precalculus, Calculus and Infinitesimals

/
3 Comments
Introduction I am convinced students learn Calculus far too late.   In my view, there has never been a good reason for this.In the US, they go through…
what are numbers

What Are Numbers?

/
7 Comments
Introduction When doing mathematics,  we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive.   Going…
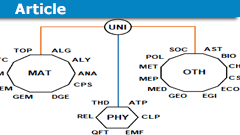
math classifications

Mathematics Fields & Applications: A Structured Guide

/
0 Comments
Introduction I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what…
evariste galois

Évariste Galois and His Theory

/
0 Comments
 * Oct. 25th, 1811  † May 31st, 1832 ... or why squaring the circle is doomed. Galois died in a duel at the age of twenty. Yet, he gave…
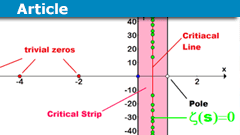
Riemann Hypothesis History

The History and Importance of the Riemann Hypothesis

/
1 Comment
Riemann Hypothesis History The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…
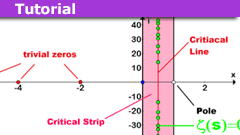
Riemann Hypothesis

The Extended Riemann Hypothesis and Ramanujan’s Sum

/
2 Comments
Riemann Hypothesis and Ramanujan's Sum ExplanationRH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line. ERH: All…
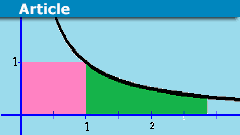
Hyperbola

The Amazing Relationship Between Integration And Euler’s Number

/
0 Comments
We use integration to measure lengths, areas, or volumes. This is a geometrical interpretation, but we want to examine an analytical interpretation that…
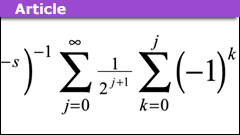
lerch and zeta functions

The Analytic Continuation of the Lerch and the Zeta Functions

/
0 Comments
Introduction In this brief Insight article the analytic continuations of the Lerch Transcendent and Riemann Zeta Functions are achieved via the Euler's…
Integral Representations of Some Special Functions

The Orin Fractional Calculus

/
8 Comments
Introduction This bit is what new thing you can learn reading this:) As for original content, I only have hope that the method of using the sets $$C_N^n:…
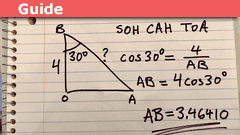
SOHCAHTOA

SOHCAHTOA: Seemingly Simple, Conceivably Complex

/
7 Comments
What is SOHCAHTOA SOHCAHTOA is a mnemonic acronym used in trigonometry to remember the relationships between the sides and angles of right triangles.…
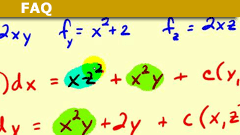
How to Find Potential Functions

How to Find a Potential Function of a Vector Field

/
0 Comments
Definition and summary Given a vector field ##\vec F(x,y,z)## that has a potential function, how do you find it? Conditions and equations $$\nabla \phi(x,y,z)…
What is a linear equation

First-Order Linear Equation: Definition & Solutions

/
0 Comments
Definition / Summary This article summarizes the first-order (linear) polynomial equation in one variable, its solution, and natural extensions to matrices…
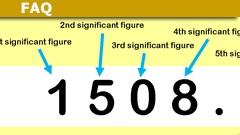
What are significant figures

Significant Figures: Rounding Rules & Examples for Science

/
0 Comments
Definition / Summary Significant figures (commonly called "sig figs") are the digits in a number that are considered when rounding a value to reflect…
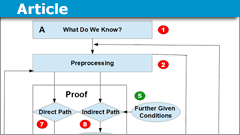
writing proofs

How to Write a Math Proof and Their Structure

/
1 Comment
Proofs in mathematics are what mathematics is all about. They are subject to entire books, created entire theories like Fermat's last theorem, are hard…
What is a fibre bundle

Fibre Bundle: Definition, Examples & Intuitive Guide

/
3 Comments
Definition / Summary Fibre bundle — intuitively, a fibre bundle is a space E that locally looks like a product B × F but may have a different global…
What are real numbers

Real Numbers: Definition, Properties & Completeness

/
0 Comments
Definition of real numbers Real numbers are the set of all values that can appear on the continuous number line. They include rational numbers (fractions…
What is a parabola

Parabola Explained: Properties, Equations & Practical Uses

/
0 Comments
What is a Parabola? A parabola is a U-shaped curve that appears frequently in mathematics, physics and engineering. It is a conic section defined by a…
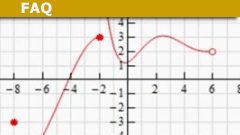
Limit of a Function

Limits of Functions for Calculus: Definition & Examples

/
0 Comments
What is a limit? In mathematics, a limit describes the behavior of a function or sequence as its input approaches a particular value. Limits are a cornerstone…
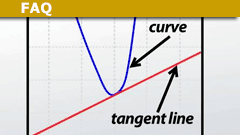
What is a Tangent Line

Tangent Line and Hyperplane: Definitions & Circle Example

/
0 Comments
Definition / Summary Informal idea The tangent to a curve in a plane at a particular point has the same gradient as the curve at that point. Generalization More…
lie algebra representations

Learn Lie Algebras: A Walkthrough – The Representations

/
1 Comment
  Part III: Representations  Sums and Products. Frobenius began in ##1896## to generalize Weber's group characters and soon investigated…
Lie Algebra Structure

Learn Lie Algebras: A Walkthrough – The Structures

/
2 Comments
  Part II: StructuresDecompositions.Lie algebra theory is to a large extend the classification of the semisimple Lie algebras which…
lie algebra basics

Learn Lie Algebras: A Walkthrough – The Basics

/
7 Comments
  Part I: Basics Introduction. This article is meant to provide a quick reference guide to Lie algebras: the terminology, important theorems,…
stock options math

Intuitive Black‑Scholes Options Pricing Explained Simply

/
19 Comments
Introduction Financial options — the right to purchase (call) or sell (put) stock or other assets at a fixed price on a future date — have been around…
selfstudy

Self-Study Roadmap: Abstract Algebra, Groups to Galois

/
4 Comments
Overview Roadmap There are three major areas of mathematics: geometry, analysis, and algebra. This insight gives a roadmap for learning basic abstract…
computers

Ramsey Theory: Foundations, Generalizations, Key Results

/
5 Comments
Ramsey theory has its origins in a very nice riddle Consider a party of 6 people. Any two of these six will either be meeting each other for the first…
selfstudyanalysis

Advanced Real Analysis: Measure & Functional Study Plan

/
14 Comments
Prerequisites If you wish to follow this guide, you should be familiar with analysis on ##\mathbb{R}## and ##\mathbb{R}^n##. See my previous insight for…
MillenniumPrize

Millennium Problems: Poincaré, P vs NP, Riemann

/
13 Comments
IntroductionWhat this Insight Covers In this Insight, I will go over the background information for the Millennium Prize problems and briefly describe…
micro3

Set-Theoretic Foundations of Numbers and Functions

/
0 Comments
Set-Theoretic Foundations of Mathematics It is important to realize that in standard mathematics we attempt to characterize everything in terms of sets.…
lineartransformations

Learn About Matrix Representations of Linear Transformations

/
19 Comments
Let X and Y be finite-dimensional vector spaces. Let ##T:X\to Y## be a linear transformation. Let ##A=(e_1,\dots,e_n)## and ##B=(f_1,\dots,f_m)## be ordered…
999equals1

Why 1 Equals 0.999… — Explanations & Rigorous Proofs

/
111 Comments
Why do people say 1 and 0.999... are equal? Aren't they two different numbers? No — 1 and 0.999... really are the same number, although that can feel…
999

Rigorous Proof: Why 0.999… Equals 1 (Geometric Series)

/
101 Comments
Yes. What 0.999... Means First, we have not addressed what 0.999... means. So it is best to first describe what the notation [tex]b_0.b_1b_2b_3...[/tex]…

Understanding Zero: History, Division, Exponents, 0!

/
7 Comments
The goal of this FAQ is to clarify the concept of 0, and specifically the operations that are allowed with it.The best way to start this FAQ is to…
ADHD studying

Overcoming Challenges of Self-Studying Number Theory

/
22 Comments
Introduction During my summer break I spent several hours each day self-studying mathematics—primarily number theory—even though I had no prior experience…