Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality per Quantum Information Theory
In her YouTube video Bell’s Theorem Experiments on Entangled Photons, Dr. Fugate shows how polarization-entangled photons violate Bell’s inequality. In this Insight, I will use quantum information theory to explain why such entangled photon-polarization qubits violate the version of Bell’s inequality due to John Clauser, Michael Horne, Abner Shimony, and Richard Holt known as the Clauser-Horne-Shimony-Holt (CHSH) inequality.
Let me start by deriving the photon-polarization qubit probabilities using Information Invariance & Continuity from the information-theoretic reconstruction of quantum mechanics, just as I did to derive the spin-##\frac{1}{2}## qubit probabilities in this Insight, this paper, and “Einstein’s Entanglement: Bell Inequalities, Relativity, and the Qubit” (Oxford UP, 2024). As with the double-slit qubit, we start with the corresponding classical configuration.
When vertically polarized light with intensity ##I_o## passes through a polarizer making an angle ##\phi## with the vertical, electromagnetism says the intensity of the light that passes through the polarizer is ##I_o\cos^2{\phi}## and that light will now be polarized along the polarizer (Analyzer) orientation (Figure 1). To create our qubit, start with a source of vertically polarized light and reduce its output to one photon at a time. If the frequency of the light is f, then the energy of each photon is hf where h is Planck’s constant. This is our photon-polarization qubit.
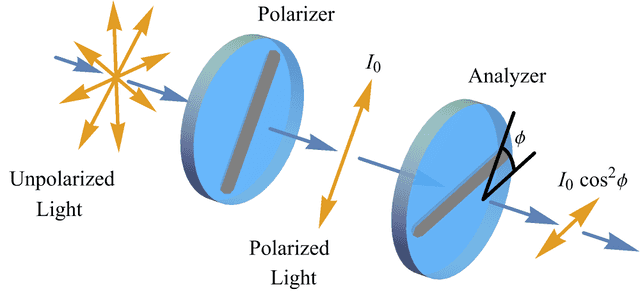
Figure 1
Now send each photon to a polarizer making an angle ##\phi## with the vertical, what does classical electromagnetism say we should find on the other side? Well, since electromagnetism says ##I_o \rightarrow I_o\cos^2{\phi}## (Figure 1), we expect ##hf \rightarrow hf\cos^2{\phi}##. But since a polarizer does not affect the frequency f of the light, that would mean Planck’s constant h has effectively been reduced to ##h\cos^2{\phi}## due to a spatial rotation of the polarizer from the vertical. This violates the observer-independence of h (per Information Invariance & Continuity) as justified by the relativity principle (“no preferred reference frame” NPRF), so quantum mechanics says we instead find each photon either passes in its entirety with probability ##P(1|\phi) = \cos^2{\phi}## or it does not pass at all with probability ##P(0|\phi) = \sin^2{\phi}## so that the average energy that passes equals ##hf\cos^2{\phi}##. That is, NPRF + h leads to the ‘average-only’ transmission of photons through polarizers just like it leads to the ‘average-only’ projection of spin angular momentum for electrons. This produces a violation of the Bell-CHSH inequality as follows.
Consider the photon-polarization Bell state in “Entangled photons, nonlocality and Bell inequalities in the undergraduate laboratory“:
##|\psi_{EPR}\rangle = \frac{|VV\rangle + |HH\rangle}{\sqrt{2}}##
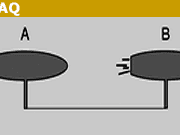
where V stands for vertical (pass) along some axis and H stands for horizontal (no pass) along that same axis. Suppose your Source produces 100 entangled photon pairs per unit time in this Bell state, sending one photon of each pair to each of Alice and Bob’s detectors. In that case, Alice and Bob’s detectors will register 100 coincident-photon-pairs per unit time (assuming perfect detection). When Alice and Bob each place a polarizer (black boxes in Dr. Fugate’s video, Figure 2) between the Source (yellow ball in Dr. Fugate’s video) and their detectors (not shown in Dr. Fugate’s video) in the plane perpendicular to the photon beam (V-H plane), each of their detectors will register 50 photons per unit time (not necessarily coincident with each other), regardless of the orientations of the polarizers. In other words, half the photons will pass and half will not pass through each polarizer, regardless of how they are oriented in the V-H plane.

Figure 2
When Alice and Bob’s polarizers are aligned, their photon detections are totally synchronized, i.e., they record 50 coincident-photon-pairs per unit time, in accord with the conservation of angular momentum. This is true for any orientation of the polarizers in the V-H plane, i.e., as with all three photon Bell triplet states, this Bell triplet state is rotationally invariant in the V-H plane. That is the physical meaning of this (and the other two) photon Bell triplet state(s). What do we expect to find when Alice and Bob choose different polarizer orientations?
Well, just as with the spin-##\frac{1}{2}## Bell triplet state (see this Insight), Alice argues that Bob’s ‘underlying’ photon polarization must be the same as hers because when Bob’s polarizer orientation is the same as hers, his photon is always V (passes) when her photon is V and his photon is always H (fails to pass) when her photon is H (again, as necessary to conserve angular momentum). So, according to Alice, when Bob’s polarizer makes an angle ##\phi## with respect to hers, his photon has a probability of ##\cos^2{\phi}## of passing through his polarizer in those trials when her photon passes through her polarizer (50% of all trials) and a probability of ##\sin^2{\phi}## of not passing through his polarizer in those trials when her photon passes through her polarizer (per ‘average-only’ transmission). That means ##P_{VV}(\phi) = \frac{1}{2}\cos^2{\phi}## and ##P_{VH}(\phi) = \frac{1}{2}\sin^2{\phi}##. Of course, Bob can make the same claim about Alice’s photon so he agrees that ##P_{VV}(\phi) = \frac{1}{2}\cos^2{\phi}## and adds ##P_{HV}(\phi) = \frac{1}{2}\sin^2{\phi}##. Normalization then says ##P_{HH}(\phi) = \frac{1}{2}\cos^2{\phi}##. In other words, the joint probabilities per NPRF + h are:
##P_{VV}(\phi) = P_{HH}(\phi) = \frac{1}{2}\cos^2{\phi}##
##P_{VH}(\phi) = P_{HV}(\phi) = \frac{1}{2}\sin^2{\phi}##
Consequently, we have Figure 3 for our photon Bell triplet state analogous to Figure 7 for our spin Bell triplet state. Figure 3 shows an example collection of eight data pairs when Alice and Bob’s measurement settings in the symmetry (V-H) plane for a photon Bell triplet state differ by ##45^{\circ}##. Alice partitions the data according to her pass (1) results to show that Bob’s measurement outcomes only average the required ##\frac{1}{2}## for conservation of angular momentum in those trials. But, when Bob partitions the data according to his pass (1) results (by switching the middle four rows of Alice’s partition as shown with blue arrows) he can show it is Alice’s measurement outcomes that only average the required ##\frac{1}{2}## for conservation of angular momentum in those trials.
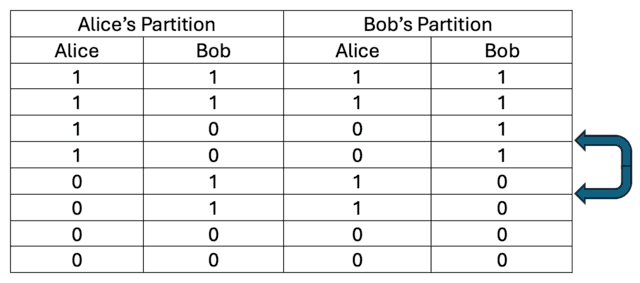
Figure 3
[Aside: These joint probabilities for the photon Bell triplet state map to Facts 1 and 2 for cases (a) and (b), respectively, for the Mermin device in this Insight if you let R = 1 and G = 0. You can change the angle in Figure 4 there to ##60^\circ## or let it remain ##120^\circ## since the result for a polarizer orientation is invariant under a ##180^\circ## rotation.] Now I will show why this violates the Bell-CHSH inequality.
Dehlinger & Mitchell start by defining
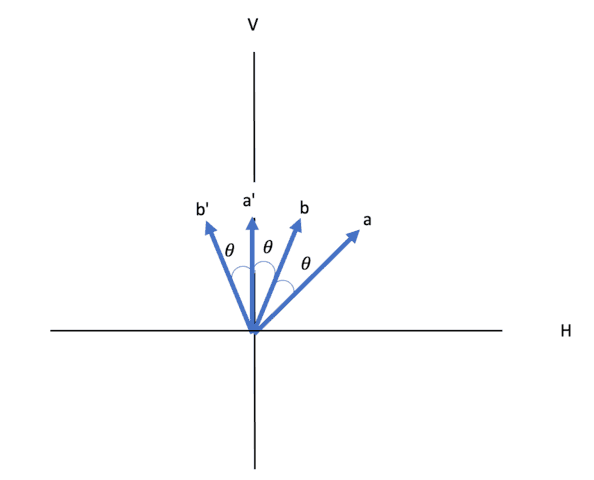
Figure 4
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018) and “Einstein’s Entanglement” (Oxford UP, 2024).








Leave a Reply
Want to join the discussion?Feel free to contribute!