You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Maxwell boltzmann: Definition and 26 Discussions
In statistical mechanics, Maxwell–Boltzmann statistics describes the average distribution of non-interacting material particles over various energy states in thermal equilibrium, and is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible.
The expected number of particles with energy
ε
i
{\displaystyle \varepsilon _{i}}
for Maxwell–Boltzmann statistics is
⟨
N
i
⟩
=
g
i
e
(
ε
i
−
μ
)
/
k
T
=
N
Z
g
i
e
−
ε
i
/
k
T
,
{\displaystyle \langle N_{i}\rangle ={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,g_{i}e^{-\varepsilon _{i}/kT},}
where:
ε
i
{\displaystyle \varepsilon _{i}}
is the energy of the i-th energy level,
⟨
N
i
⟩
{\displaystyle \langle N_{i}\rangle }
is the average number of particles in the set of states with energy
ε
i
{\displaystyle \varepsilon _{i}}
,
g
i
{\displaystyle g_{i}}
is the degeneracy of energy level i, that is, the number of states with energy
ε
i
{\displaystyle \varepsilon _{i}}
which may nevertheless be distinguished from each other by some other means,
μ is the chemical potential,
k is Boltzmann's constant,
T is absolute temperature,
N is the total number of particles:
Z is the partition function:
e is Euler's numberEquivalently, the number of particles is sometimes expressed as
⟨
N
i
⟩
=
1
e
(
ε
i
−
μ
)
/
k
T
=
N
Z
e
−
ε
i
/
k
T
,
{\displaystyle \langle N_{i}\rangle ={\frac {1}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,e^{-\varepsilon _{i}/kT},}
where the index i now specifies a particular state rather than the set of all states with energy
ε
i
{\displaystyle \varepsilon _{i}}
, and
Z
=
∑
i
e
−
ε
i
/
k
T
{\textstyle Z=\sum _{i}e^{-\varepsilon _{i}/kT}}
.
View More On Wikipedia.org
The expected number of particles with energy
ε
i
{\displaystyle \varepsilon _{i}}
for Maxwell–Boltzmann statistics is
⟨
N
i
⟩
=
g
i
e
(
ε
i
−
μ
)
/
k
T
=
N
Z
g
i
e
−
ε
i
/
k
T
,
{\displaystyle \langle N_{i}\rangle ={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,g_{i}e^{-\varepsilon _{i}/kT},}
where:
ε
i
{\displaystyle \varepsilon _{i}}
is the energy of the i-th energy level,
⟨
N
i
⟩
{\displaystyle \langle N_{i}\rangle }
is the average number of particles in the set of states with energy
ε
i
{\displaystyle \varepsilon _{i}}
,
g
i
{\displaystyle g_{i}}
is the degeneracy of energy level i, that is, the number of states with energy
ε
i
{\displaystyle \varepsilon _{i}}
which may nevertheless be distinguished from each other by some other means,
μ is the chemical potential,
k is Boltzmann's constant,
T is absolute temperature,
N is the total number of particles:
Z is the partition function:
e is Euler's numberEquivalently, the number of particles is sometimes expressed as
⟨
N
i
⟩
=
1
e
(
ε
i
−
μ
)
/
k
T
=
N
Z
e
−
ε
i
/
k
T
,
{\displaystyle \langle N_{i}\rangle ={\frac {1}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,e^{-\varepsilon _{i}/kT},}
where the index i now specifies a particular state rather than the set of all states with energy
ε
i
{\displaystyle \varepsilon _{i}}
, and
Z
=
∑
i
e
−
ε
i
/
k
T
{\textstyle Z=\sum _{i}e^{-\varepsilon _{i}/kT}}
.
View More On Wikipedia.org
-

B Shape & Dimensions of Containers: Impact on the Maxwell Boltzmann Distribution
1.Does the Maxwell Boltzmann distribution change depending on the shape of the container? Pressure and the volume is constant. How is the Distribution affected whether the gas is in: a,sphere b,cube c,cuboid? Why does/doesn’t the distribution change depending on the shape of the container...- sol47739
- Thread
- Replies: 1
- Forum: Classical Physics
-

I Maxwell Boltzmann distribution
In the Aschcroft & Mermin solid state book there is a curve to compare F.D and M.B distribution. I can't understand the concept of M.B curve; what does mean exactlly when x =0? It means the probability of zero energy for particles is most or ...?- Rzbs
- Thread
- Replies: 5
- Forum: Atomic and Condensed Matter
-
J
I Value of beta in Boltzmann Statistics taking degeneracy into account
Hello, The relationship between entropy ##S##, the total number of particles ##N##, the total energy ##U(β)##, the partition function ##Z(β## and a yet to be defined constant ##β## is: $$S(\beta)=k_BN \cdot \ln(Z(\beta)) - \beta k_B \cdot U(\beta)$$ Which leads to: $$\frac{dS}{d\beta} =...- JohnnyGui
- Thread
- Replies: 19
- Forum: Quantum Physics
-
S
Using Maxwell-Boltzman Statistics
Homework Statement Determine if the classical approximation (Maxwell-Boltzman statistics) could be employed for the following case: a) Electron gas in a metal at 2.7K (cubic metal lattice of spacing 2Å) Homework Equations Maxwell-Boltzman statistics are acceptable to use if the de broglie...- says
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-
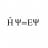
Ideal gas pressure from Maxwell-Boltzmann distribution
Hi everyone I'm having trouble with solving an exercise in statistical physics. I need to argue why the average number of particles with a velocity between ##v## and ##v+dv## that hit a surface area ##A## on the container wall in a time interval ##\Delta t## is $$N_{collision}=v_{x}A\Delta t...- H Psi equal E Psi
- Thread
- Replies: 4
- Forum: Electromagnetism
-

Maxwellian velocity distribution vs. speed distribution
Maxwellian velocity distribution is obtained by $$g(v_x)\propto e^{-mv_x^2/2k_B T}$$ and when extended to 3 dimensions the distribution becomes: $$\propto e^{-mv_x^2/2k_B T}e^{-mv_y^2/2k_B T}e^{-mv_z^2/2k_B T} = e^{-mv^2/2k_B T}$$ Now looking at the speed distribution we take a spherical shell...- weezy
- Thread
- Replies: 3
- Forum: Electromagnetism
-
R
What's the nature of a force acting on this gas? (Thermo)
Homework Statement A gas in equilibrium has distribution function: f(p,r) = C0*(1+y*x)(2*pi*m*k*T)-3/2*exp(-p2/(2*m*k*T)) where x is the distance along an axis with fixed origin, and y is a constant. What's the nature of the force acting on this gas? Homework Equations Maxwell bolztmann...- Raynor49
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
Average Speed for Maxwell's Distribution of Molecular Speed
Using the Maxwell-Boltzmann equation above, there is an example in my book (Giancoli 4th edition p. 481) where they use this to find the average velocity. I understand that it would just be the sum of all the speeds of the molecules divided by the number of molecules. But then I'm having...- RaulTheUCSCSlug
- Thread
- Replies: 2
- Forum: Electromagnetism
-
C
Why does corrected Maxwell Boltzmann have decimals?
So I have just been reading up on statistical thermodynamics and have no idea why the bose-einstein, fermi dirac and maxwell boltzman are all integers, that makes sense, but then when you make the degenerate correction to the maxwell Boltzmann by dividing by N! we get decimal answers. Why is...- cooev769
- Thread
- Replies: 2
- Forum: Atomic and Condensed Matter
-
R
A heating element in a container with low pressure gas?
This is just a qualitative question but feel free to show an equation if possible. Basically if you have a container with a heating element, let's say 500 W with a temperature of 2500 Kelvins and inside this box is a low pressure ideal gas, something like 1/100 of an atmosphere. Also imagine...- randombill
- Thread
- Replies: 7
- Forum: Thermodynamics
-
J
Maxwell-Boltzmann Spherical Cap
Homework Statement An ideal gas satisfying the Maxwell-Boltzmann distribution is leaking from a container of the volume V through a circular hole of area A'. The gas is kept in the container under pressure P and temperature T. The initial number density (concentration) is given by n0=N/V...- J_M_R
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
L
Maxwell-Boltzmann distribution help
Homework Statement Use the Maxwell-Boltzmann distribution of speeds to find the fraction of F2 molecules at 500 K which have speeds in the range 240 to 250 m s -1 (HINT: determine the fraction of the total area under the distribution curve represented by the part between these two speeds...- Lily Wright
- Thread
- Replies: 3
- Forum: Introductory Physics Homework Help
-
G
Derivative Maxwell boltzmann distribution
Homework Statement i need to show that the peak of the maxwell Boltzmann distribution is equal to 1/2 kt. Homework Equations maxwell Boltzmann distribution according to modern physics 3rd edition by kenneth kramer. ill try to do my best with this N(E)= \frac{2N}{√∏}...- giraffe
- Thread
- Replies: 7
- Forum: Advanced Physics Homework Help
-
T
Maxwell Boltzmann Distribution
I don't know how to integrate the Maxwell-Boltzmann distribution without approximation or help from Maple. Given the Maxwell-Boltzmann distribution: f(v) = 4\pi\left[\frac{m}{2\pi kT}\right]^{3/2}v^2\textrm{exp}\left[\frac{-mv^2}{2kT}\right] Observe the appearance of the Boltzmann factor...- TeslaPow
- Thread
- Replies: 11
- Forum: Electromagnetism
-
T
Maxwell Boltzmann Distribution
I don't know how to integrate the Maxwell-Boltzmann distribution without approximation or help from Maple. Given the Maxwell-Boltzmann distribution: f(v) = 4*pi*[m/(2*pi*k*T)]^(3/2)*v^2*exp[(-m*v^2)/(2*k*T)] Observe the appearance of the Boltzmann factor exp[(-m*v^2)/(2*k*T)] with E =...- TeslaPow
- Thread
- Replies: 2
- Forum: Electromagnetism
-
M
Maxwell boltzmann distribution
The question is in the image file. I am stuck, I don't know how to start. Can someone guide me please?- MissP.25_5
- Thread
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-
D
Using Maxwell Boltzmann distribution to find number of atoms
Homework Statement You will recall from our discussion of the Franck-Hertz experiment that the energy difference between the first excited state of mercury and the ground state is 4.86 eV. If a sample of mercury vaporized in a flame contains 1.06×1020 atoms in thermal equilibrium at 1563 K...- dinospamoni
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
Probability distribution using the Maxwell Boltzmann formula
According the the kinetic theory of gases, molecules moving along the x direction are given by Σx= (1/2) mv^2, where m = mass and vx is the velocity in the x direction The distribution of particles over velocities is given by the Boltzmann law p(x)=e^[(-mv^2)/ekT] where velocities range from...- Sonor@12
- Thread
- Replies: 2
- Forum: Electromagnetism
-
T
How to derivate Maxwell Boltzmann Distribution
Hi PFers. I am interested in Maxwell Boltzmann Distribution. I have searched in Internet for the derivation but I am not satified with them. Can somebody show me the way to derivate it? Thanks. ψ(v)=(m/2*pi*kT)^(3/2) e^(-mv^2/2kT)- Troller
- Thread
- Replies: 4
- Forum: Electromagnetism
-
R
Maxwell Boltzmann Speed Distribution
Homework Statement The three quantities Vmost probable, Vaverage, and Vrms, are not the same for the Maxwell speed distribution in 3D. If you restrict the gas to only be one dimensional, are these three quantities equal to each other? Justify your answer with a short explanation. Homework...- ramsharmjarm
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-
J
Application of Maxwell Boltzmann velocity distribution to nanoscale systems
Dear All I have a question about the validity of Maxwell Boltzmann velocity distribution in the case of nanoscale systems. When you consider a nanoscale system such as flow of water molecules (less than 100 molecules) through a carbon nanotube or graphene sheet, is it possible to expect a...- jeetu
- Thread
- Replies: 1
- Forum: Electromagnetism
-
J
Strange maxwell boltzmann statistics, what is it actually?
Originally, it is derived from the weight of a confuguration,i.e. how electrons are distributied in different energy level:n=gexp(a+be) It gives the number of electrons in each energy level.However suddenly it can be apply to a cloud of gas?? By dividing a box of gas into different energy and...- jessicaw
- Thread
- Replies: 4
- Forum: Electromagnetism
-
S
Physical Chemistry- Maxwell Boltzmann Distribution
Homework Statement Use the maxwell Boltzmann distribution to derive an expression for <v^3> Homework Equations <v>=(8RT/piM)^1/2 The Attempt at a Solution I know that you have to integrate from 0 to infinity v^3p(v)dv.. but I don't really know how to integrate this. I just need to...- sdoyle1
- Thread
- Replies: 1
- Forum: Biology and Chemistry Homework Help
-
C
Maxwell Boltzmann Distribution Question
Hello everyone Homework Statement The equivalent of the Maxwell-Boltzman distribution for a two-dimensional gas is P(v) = Cv e^-\frac {mv^2}{kt} Determine C so that \int_0^\infty P(v)dv = NHomework Equations Not really sureThe Attempt at a Solution I wasn't really sure how to tackle this...- Crosshash
- Thread
- Replies: 7
- Forum: Introductory Physics Homework Help
-
V
Maxwell Boltzmann distribution
Homework Statement The energy difference between the first excited state of mercury and the ground state is 4.86 eV. (a) If a sample of mercury vaporized in a flame contains 10^20 atoms in thermal equilibrium at 1600K, calculate the number of atoms in the n=1 (ground) and n=2 (first-excited)...- vincisonfire
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-
C
Fermi Dirac (FD) and Maxwell Boltzmann (MB)
I have a homework problem that asks me to interpret the two curves for when the Fermi level (Ef) is 0.25 eV. I ploted the two graphs and both of them look nothing alike when E < Ef. But both plots predict a probability of essentially zero when E > Ef. I was wondering why is there such a large...- Corneo
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help