multiplicity Definition and 78 Threads

In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial has a root at a given point is the multiplicity of that root.
The notion of multiplicity is important to be able to count correctly without specifying exceptions (for example, double roots counted twice). Hence the expression, "counted with multiplicity".
If multiplicity is ignored, this may be emphasized by counting the number of distinct elements, as in "the number of distinct roots". However, whenever a set (as opposed to multiset) is formed, multiplicity is automatically ignored, without requiring use of the term "distinct".

View More On Wikipedia.org
Recent contents Top users
  1. phos19

    I Fermi energy for a Fermion gas with a multiplicity function ##g_n##

    I ran across the following problem : Statement: Consider a gas of ## N ## fermions and suppose that each energy level ## \varepsilon_n## has a multiplicity of ## g_n = (n+1)^2 ##. What is the Fermi energy and the average energy of this gas when ## N \rightarrow \infty## ? My attempt: The...
  2. V9999

    I A doubt about the multiplicity of polynomials in two variables

    Let ##P(x,y)## be a multivariable polynomial equation given by $$P(x,y)=52+50x^{2}-20x(1+12y)+8y(31+61y)+(1+2y)(-120+124+488y)=0,$$ which is zero at ##q=\left(-1, -\frac{1}{2}\right)##. That is to say, $$ P(q)=P\left(-1, -\frac{1}{2}\right)=0.$$ My doubts relie on the multiplicity of this point...
  3. B

    A Can we have molecular transitions that change multiplicity?

    Hello! Can we have molecular transitions (not restricted to electric dipole) that change the multiplicity of the electronic level i.e. ##2S+1##. For electric dipole that is strictly forbidden. For magnetic dipole, we have a term in the operator of the form ##S\cdot B## and assuming the B is...
  4. F

    MHB What are the requirements for the exercise on multiplicity and set of zeros?

  5. O

    Chemistry 1H NMR: Unsymmetric Peak Multiplicity and J Values

    The peaks all look unfamiliar, no symmetry, or very little, and they all integrate to a small number of hydrogen while being surrounded by a large number. Here are the images.1.) 2.) 3.) 4.) 5.) Thanks for any explanations. I don't expect anyone to do it for me, I just have no other...
  6. E

    Why is the NMR multiplicity incorrect in some places?

    I was doing a question that wanted you to determine the structure given a molecular formula and an NMR spectrum. The following was the answer: I'm unsure as to how the multiplicities were obtained. For ##X##, the neighbouring carbon ##Y## has 2 hydrogens, so this peak is a triplet (OK so far!)...
  7. F

    Energy of an ideal gas given its multiplicity

    Question: The multiplicity of an ideal gas is given by g(U) = A.U3N/2, where U is the energy of the gas, A is a constant and N is the number of particles in the gas. Prove that the energy of the gas given a temperature T is U = (3/2).N.kb.T Attempts: My first thought was to...
  8. M

    Thermodynamics: (Entropy) Multiplicity using hypercube

    Hello, Few years back I was reading about calculating multiplicity using hypercube (n-cube). Multiplicity was normalized using this method. I wanted to read it again but I just cannot find it now. I tried every combination of keywords. I remember it was a Wikipedia link. Any help would be...
  9. G

    Local Algebra: intersection multiplicity

    I'm trying to understand why the intersection multiplicity of two singular subvarieties is not equal to the complex dimension of the local ring but it is instead the Euler characteristic. Is it possible to find an intuitive explanation? I think that the following concepts need some...
  10. Dethrone

    MHB Exploring Algebraic Multiplicity: Solving 5a and b with Hints for 5c

    5a and b are quite trivial. I have no idea how to do 5c). Any hints?
  11. V

    Algebraic Multiplicity of an Eigenvalue

    Please have a look at the attached images.I am attempting a proof for the statement : The algebraic multiplicity of an eigen value λ is equal to dim null [T - λ I] dim V. Please advise me on how to move ahead. Apparently, I am at the final inference required for a proof but unable to move...
  12. camilus

    Multiplicity free fibers in maps between vector bundles

    For a map between vector bundles (which commute with a certain Lie groups like Sl2R or GL2R), what does it mean exactly for a fiber to be multiplicity free? Eplanations would be good, but examples would be even better. Thanks in advance, Gauss bless you! CM
  13. T

    Statistics: Degeneracy and Multiplicity

    Homework Statement Consider drawing one card from a deck with no jokers or other special cards. a) What is the number of microstates? (4/13/52/cant tell) b) What is the number of macrostates?(4/13/52/cant tell) c) What is the degeneracy of macrostate spade? (4/13/52/cant tell) d) What is the...
  14. WannabeNewton

    Calculating Multiplicity of N Hard Sphere Gases

    Hi guys. Consider the problem of calculating the multiplicity (phase space volume) of N hard sphere gases each of whose center of mass is confined to a volume V. The spheres themselves have volume ##\omega## and do not interact with one another in equilibrium time scales. Then ##\Omega \propto...
  15. F

    MHB What Is Intersection Multiplicity and How Is It Calculated?

    Define the multiplicity of $f$ at $p$ and the interesction multiplicity of $f,g$ at $p$. Let curves $A$ and $B$ be defined by $x^2-3x+y^2=0$ and $x^2-6x+10y^2=0$. Find the intersection multiplicities of all points of intersection of $A$ and $B$. If we let $f=x^2-3x+y^2$ and $g=x^2-6x+10y^2$...
  16. L

    Interpretation of Multiplicity Function

    Hi. I am trying to understand the multiplicity function Ω!/L!(Ω-L)! where Ω= number of boxes and L= number of distinguishable boxes. I just want a simple intuitive explanation. I have seen a couple of these but none of them ever stick. The term that confuses me the most is the (Ω-L)! Any help...
  17. P

    MHB Find the zeros of the polynomial function and state the multiplicity of each

    f(x)= x (x+2)^2 (x-1)^4Zeros would be: 0, -2, 1 Multipicity of : 1 2 4Then for y- intercept: f(0)=0 And don't know how to graph it...
  18. P

    MHB Help finding multiplicity and zeros?

    (x+4) (x-2)^3 (x^2+2x-8) would it be -4 multiplicity of 2 and 2 multiplicity of 4?
  19. F

    MHB Using Multiple Eigenvectors for the Same Eigenvalue

    I am trying to prove the spectral decomposition theorem for normal compact operators. Now, my book says the space H is the closure of the direct sum of $F_{t}$ where we the $F_{t}$ are eigenspaces and we sum over all eigenvalues $t$. My question concerns what happens when there are 2 linearly...
  20. mishima

    Total multiplicity is product of individual multiplicities?

    Hi, I was looking for a proof or explanation of this. From Schroeder's Thermal Physics, pg 56, explaining interacting systems in equilibrium. The example in the text is two 3-harmonic oscillators with a total of 6 units of energy. So one macrostate is where each has 3 units of energy. The...
  21. S

    How Does the Multiplicity of a Classical Gas Relate to Ideal Gas Conditions?

    Homework Statement Consider the multiplicity of a classical gas of N non-interacting molecules (not necessarily monatomic). Since they don't interact,their positions are not correlated, so the multiplicity of each will be simply proportional to the volume, with the result that the total...
  22. D

    Multiplicity of a two state system

    I only have a doubt about which definition to use for the multiplicity of a two state system. Clearly the total multiplicity of a two state system is given by: Ω=2^N, but what about the definition: Ω(N,n) = \binom{N}{n} = \frac{N!}{n!\cdot(N-n)!}. Clearly: 2^N ≠...
  23. G

    Real Analysis: Proof about simple zeros (multiplicity = 1)

    Homework Statement A function f has a simple zero (or zero of multiplicity 1) at x0 if f is differentiable in a neighborhood of x0 and f(x0) = 0 while f(x0) ≠ 0. Prove that f has a simple zero at x0 iff f(x) = g(x)(x - x0), where g is continuous at x0 and differentiable in a deleted...
  24. B

    Is the geometric multiplicity of an eigenvalue a similar invariant?

    If two matrices similar to one another are diagonalizable, then certainly this is the case, since the algebraic multiplicity of any eigenvalue they share must be equal (since they are similar), and since they are diagonalizable, those algebraic multiplicities must equal the geometric...
  25. B

    When is algebraic multiplicity = geometric multiplicity?

    In my last Linear Algebra class we saw Eigenvalues and Diagonalizations. It turns out that an n x n matrix is diagonalizable if its eigenbasis has n linearly independent vectors. If the characteristic equation for the matrix is (λ - λ_1)^{e_1}(λ - λ_2)^{e_2}...(λ - λ_k)^{e_k} = 0 then 1)...
  26. N

    What is an Example of a Matrix with Geometric Multiplicity Greater Than 1?

    after finding out what geometric multiplicity was, I was surprised to notice that in every question I'd done it was always 1. So I'm trying to prove an example with g.m. > 1 to see why it works. I've found a matrix which definitely has an eigenvalue with g.m. = 2. I've checked everything with...
  27. D

    Geometric Multiplicity of Eigenvalues

    Could someone please explain to me (with an example if possible) what is the Geometric Multiplicity of Eigenvalues? I cannot understand it from what I have read on the web till now. Thanks in advance.
  28. I

    MHB How to prove sequence converges quadratically to a root of multiplicity

    A function f has a root of multiplicity $m>1$ at the point $ x_*$ if $f(x_*)=f'(x_*)=...=f^{(m-1)}(x_*)=0$. Assume that the iteration$ x_{k+1}=x_k-mf(x_k)/f'(x_k)$ converges to $x_*$. If$ f^{(m)}(x_*)≠0$, prove that this sequence converges quadratically.(We may use the Taylor's series, but I...
  29. X

    Finding the eigenvectors of a 2nd multiplicity engenvalue

    Homework Statement I'm given this matrice 2 1 0 1 2 0 0 0 3 and I need to find it's eigenvectors Homework Equations The Attempt at a Solution So I get the eigenvalues to be 1,3,3 with 3 being the one with...
  30. V

    Multiplicity of an eigen value , k = dim[ Null(T - k I)^( dim V) ]

    Homework Statement Prove without induction that Multiplicity of an eigen value , k = dim[ Null(T - k I)^( dim V) ] Homework Equations [(T - k I)^dim V ] v =0 [Thoughts] i understand that normal eigen vectors with same eigen values may not be linearly independent. [(T - k...
  31. A

    Multiplicity of particles on a lattice

    Homework Statement A particle can exist in three microstates, with energies E0 < E1 < E2. Consider N >> 1 such particles, fixed on a lattice. There are now n0 particles with energy E0, n1 particles with energy E1 and n2 = N - n0 - n1 particles with energy E2. We have that n_j >> 1 for j = 0...
  32. N

    Algebraic Multiplicity of Eigenvalues Question?

    Homework Statement Let \vec{x} and \vec{v} be vectors in \mathbb{R}^3. If A is a matrix such that A\vec{x} gives the projection of \vec{x} onto \vec{v}, then what are the eigenvalues of A and what are their algebraic multiplicities? Homework Equations Eigenvalue: A real number λ is an...
  33. W

    Analysis: Potentially flawed proof in book describing roots of multiplicity m

    Homework Statement In the book "Friendly introduction to analysis, 2nd Ed." by kosmala there is a definition of the root of a function and subsequent theorem and proof. Either the proof is not directly addressing certain important properties, or is flawed. The definition and theorem are as...
  34. S

    Multiplicity and Inverse of probability distribution, what do they mean?

    Hello Everybody. I have a rather simple question, which still kept me thinking for two hours without any result. If we want to determine the multiplicity in the microcanonical ensemble we just divide the volume of the shell containing the accessible microstates over the volume of one...
  35. H

    Why is the geometric multiplicity more or equal to 1?

    Hi. I've got a theoretical doubt: why is the geometric multiplicity more or equal to 1? Couldn't happen that the eigenspace is the null vector? Thanks!
  36. S

    How to determine which eigenvalue has multiplicity 2 ?

    Say I have a 4x4 matrix and I know 3 eigenvalues and the 3 corresponding eigenvectors. Is there a fast way to calculate which one has multiplicity 2 without calculating the characteristic polynomial(too time consuming for a 4x4 matrix) or without determining the dimensions of (A-λ I) for each...
  37. S

    Which eigenvalue has multiplicity greater than 1 ?

    http://dl.dropbox.com/u/33103477/question.png I have determined the eigenvalues which are -2, 2 and 1 respectively. I'm pretty sure that the one with multiplicity of 2 is the, the eigenvalue = 2 as it occur's twice in the diagnol. But I don't think that's a concrete enough reason. Any...
  38. I

    Multiplicity of Eigenvalues in a 3x3 Matrix

    Homework Statement The matrix A = \begin {bmatrix} 0 & -1 & 0 \\ 0 & -1 & 0 \\ 0 & 1 & 0 \end{bmatrix} has two real eigenvalues, one of multiplicity 2 and one of multiplicity 1. Find the eigenvalues and a basis of each eigenspace.Homework Equations N/AThe Attempt at a Solution I've done...
  39. S

    Algebraic multiplicity of the matrix

    The algebraic multiplicity of the matrix [ 0 1 0 ] [ 0 0 1 ] [ 1 -3 3 ] options : a.1 b.2 c.3 d.4 i don get the question first, somebody help me...
  40. S

    Algebraic multiplicity of matrix

    hi friends please help in finding out the ans for this . A 3x3 matrix was given , am asked to find algebraic multiplicity of it ! how to find algebraic multiplicity of 3x3 matrix ??
  41. Z

    Multiplicity of an Einstein solid

    Okay, I am not sure if this is the right subforum, but here goes: An einstein solid is a solid composed of N quantum harmonic oscillators, which can store evenly spaced energy units q. Now suppose we have an einstein solid of N oscillators with q energy units, where q>>N. My book wants to...
  42. S

    Statistical mechanics: multiplicity

    Homework Statement We have a surface that can adsorb identical atoms. There are N possible adsorption positions on this surface and only 1 atom can adsorb on each of those. An adsorbed atom is bound to the surface with negative energy -\epsilon (so \epsilon > 0). The adsorption positions are...
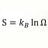
  43. morrobay

    S = k ln W : ln : From Both Multiplicity and Integral ?

    Can the natural logarithm in the statistical mechanics formulation of entropy , S = k ln W be based on both multiplicity and an integral ? The extensive property and multiplicity explanation : That for any given macrostate , the total entropy of two interacting systems is the sum of their...
  44. T

    Geometric multiplicity of an eigenvalue

    Say we have an eigenvalue \lambda and corresponding eigenvectors of the form (x,x,2x)^T. What is the geometric multiplicity?
  45. S

    Jordan Forms, Algebraic and Geometric Multiplicity

    Homework Statement A 20 × 20 matrix C has characteristic polynomial (λ^2 − 4)^10. It is given that ker(C−2I), ker (C − 2I)^2, ker (C −2I)^3 and ker (C −2I)^4 have dimensions 3,6,8,10 respectively. It is given that ker (C + 2I), ker (C +2I)^2, ker (C +2I)^3 and ker (C +2I)^4 have di- mensions...
  46. Q

    Multiplicity of Macrostates, involving dice

    I didn't really know where the proper place was for this, but this is an intro thermodynamics class and I'm really confused over this math question (it's not strictly physics-related). Homework Statement Consider rolling N six-sided dice. Define a microstate as the number showing on...
  47. C

    What is the geometric multiplicity of \lambda=0 as an eigenvalue of A?

    Homework Statement \lambda=0 is an eigenvalue of A= |1 1 1 1 1| |1 1 1 1 1| |1 1 1 1 1| |1 1 1 1 1| |1 1 1 1 1| Homework Equations Find the geometric multiplicity of \lambda=0 as an eigenvalue of A The Attempt at a Solution I row reduced it then got the last four rows of all 0s...
  48. E

    Sterling approximation, multiplicity, and two-state paramagnet

    Homework Statement For a single large two-state paramagnet, the multiplicity function is very sharply peaked about N_{\uparrow} = N/2. (a) Use Stirling's approximation to estimate the height of the peak in the multiplicity function. (I am fairly confident in my answer here) (b) Use the...
  49. W

    Linear Algebra / Geomtric Multiplicity

    Homework Statement Let A = a 2x2 matrix row 1 [3/2 ½ ] row 2 [-½ ½] a) Find the eigenvalue(s) of A b) Find the algebraic multiplicity of each eigenvalue. c)Find the geometric multiplicity of each eigenvalue. Homework Equations The Attempt at a Solution I found the...
  50. K

    Multiplicity for 3 Dimensional problem

    Homework Statement I am having trouble finding an expression for W (multiplicity) for a chain that can move in all possible directions (3 dimensions) Homework Equations Multiplicity is the number of possible states over total states. The Attempt at a Solution\ I understand for a...
Back
Top