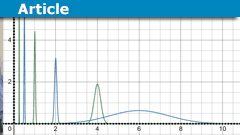
What Exactly is Dirac’s Delta Function?
/
1 Comment
Introduction: "Convenient Notation"In Dirac's Principles of Quantum Mechanics published in 1930 he introduced a "convenient notation" he referred …

Fixing Things Which Can Go Wrong With Complex Numbers
Abstract
This article will build on the hints about treating the complex numbers as a branched surface, briefly described and pictured in section 4.2…

Fermat’s Last Theorem
Abstract
Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states…
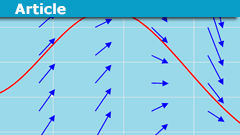
Vector Spaces: Concepts, History, and Applications Guide
The Concept
A vector space is an additively written abelian group together with a field that operates on it.Intuitive picture vs abstract definition
Vector…

The Many Faces of Topology
Abstract
Topology as a branch of mathematics is a bracket that encompasses many different parts of mathematics. It is sometimes even difficult to see…
Brownian Motions and Quantifying Randomness in Physical Systems
Stochastic calculus has come a long way since Robert Brown described the motion of pollen through a microscope in 1827. It's now a key player in data science,…

Views On Complex Numbers
Abstract
Why do we need yet another article about complex numbers? This is a valid question and I have asked it myself. I could mention that I wanted…

The Lambert W Function in Finance
Preamble
The classical mathematician practically by instinct views the continuous process as the "real" process, and the discrete process as an approximation…

Why Division by Zero is a Bad Idea
A division by zero is primarily an algebraic question. The reasoning therefore follows the indirect pattern of most algebraic proofs:
What if it was allowed?
Then…
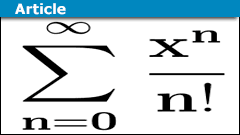
Series in Mathematics: From Zeno to Quantum Theory
Introduction
Series play a decisive role in many branches of mathematics. They accompanied mathematical developments from Zeno of Elea (##5##-th century…

Differential Equation Systems and Nature
Abstract
"Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…

Beginners Guide to Precalculus, Calculus and Infinitesimals
Introduction
I am convinced students learn Calculus far too late. In my view, there has never been a good reason for this.In the US, they go through…

What Are Numbers?
Introduction
When doing mathematics, we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive. Going…

Introduction to the World of Algebras
Abstract
Richard Pierce describes the intention of his book [2] about associative algebras as his attempt to prove that there is algebra after Galois…

What Are Infinitesimals – Advanced Version
Introduction
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…

An Overview of Complex Differentiation and Integration
Abstract
I want to shed some light on complex analysis without getting all the technical details in the way which are necessary for the precise treatments…

When Lie Groups Became Physics
Abstract
We explain by simple examples (one-parameter Lie groups), partly in the original language, and along the historical papers of Sophus Lie, Abraham…
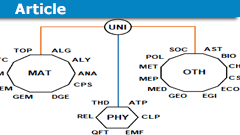
Mathematics Fields & Applications: A Structured Guide
Introduction
I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what…

Counting to p-adic Calculus: All Number Systems That We Have
An entire book could easily be written about the history of numbers from ancient Babylon and India, over Abu Dscha'far Muhammad ibn Musa al-Chwarizmi (##\sim…

Évariste Galois and His Theory
* Oct. 25th, 1811 † May 31st, 1832
... or why squaring the circle is doomed.
Galois died in a duel at the age of twenty. Yet, he gave…
Yardsticks to Metric Tensor Fields
I asked myself why different scientists understand the same thing seemingly differently, especially the concept of a metric tensor. If we ask a topologist,…
P vs. NP and what is a Turing Machine (TM)?
P or NP
This article deals with the complexity of calculations and in particular the meaning of
##P\stackrel{?}{\neq}NP##
Before we explain what P and…
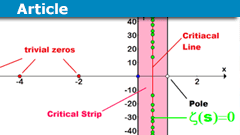
The History and Importance of the Riemann Hypothesis
Riemann Hypothesis History
The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…
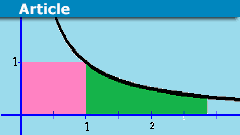
The Amazing Relationship Between Integration And Euler’s Number
We use integration to measure lengths, areas, or volumes. This is a geometrical interpretation, but we want to examine an analytical interpretation that…

Probabilistic Factors Involved in Disease and Virus Testing
Introduction
This Insight looks at the various probabilistic factors and related terminology involved in disease and virus testing.As we all know,…

10 Math Things We All Learnt Wrong At School
Some of these could even lead to heavy debates within the scientific community, so maybe I should say: from my point of view. So before you get excited…

How Bayesian Inference Works in the Context of Science
Confessions of a moderate Bayesian part 3
Read part 1: How to Get Started with Bayesian Statistics
Read part 2: Frequentist Probability vs Bayesian ProbabilityBayesian…
Exploring Frequentist Probability vs Bayesian Probability
Confessions of a moderate Bayesian, part 2
Read Part 1: Confessions of a moderate Bayesian, part 1Bayesian statistics by and for non-statisticianshttps://www.cafepress.com/physicsforums.13280237
Background
One…
How to Get Started with Bayesian Statistics
Confessions of a moderate Bayesian, part 1
Bayesian statistics by and for non-statisticianshttps://www.cafepress.com/physicsforums.13265286
Background
I…

Mary Somerville: Scottish Polymath & RAS Honorary Member
Mary Somerville & Caroline Herschel: Google DoodleGoogle Doodle: Mary Somerville and Caroline Herschel
The Google Doodle for 2 February 2020 celebrated…
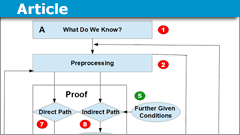
How to Write a Math Proof and Their Structure
Proofs in mathematics are what mathematics is all about. They are subject to entire books, created entire theories like Fermat's last theorem, are hard…
A Pure Hamiltonian Proof of the Maupertuis Principle
Here is another version of proof of Maupertuis's principle. This version is pure Hamiltonian and independent of the Lagrangian approach.The proof…

The Sum of Geometric Series from Probability Theory
Here I present a simple (but to the best of my knowledge, new) derivation of the formula for the sum of the infinite geometric series. The derivation is…

Learn Lie Algebras: A Walkthrough – The Representations
Part III: Representations
Sums and Products.
Frobenius began in ##1896## to generalize Weber's group characters and soon investigated…

Learn Lie Algebras: A Walkthrough – The Structures
Part II: StructuresDecompositions.Lie algebra theory is to a large extend the classification of the semisimple Lie algebras which…

Learn Lie Algebras: A Walkthrough – The Basics
Part I: Basics
Introduction.
This article is meant to provide a quick reference guide to Lie algebras: the terminology, important theorems,…

Intuitive Black‑Scholes Options Pricing Explained Simply
Introduction
Financial options — the right to purchase (call) or sell (put) stock or other assets at a fixed price on a future date — have been around…
Learn the Basics of Hilbert Spaces and Their Relatives: Operators
Operators. The Maze Of Definitions.
We will use the conventions of part I (Basics), which are ##\mathbb{F}\in \{\mathbb{R},\mathbb{C}\}##,…
Learn the Basics of Hilbert Spaces and Their Relatives: Definitions
Basics
Language first: There is no such thing as the Hilbert space.Hilbert spaces can look rather different, and which one is used in…

Learn About Intransitive Dice with a Twist
Intransitive dice are sets of dice that don't follow the usual rules for "is better/larger than". If A<B and B<C, then A<C. If Bob runs faster…

A Journey to The Manifold SU(2): Differentiation, Spheres, and Fiber Bundles
Part 2
Differentiation, Spheres, and Fiber Bundles
Image source: [24]The special unitary groups play a significant role in the standard…

How to Tell Operations, Operators, Functionals, and Representations Apart
All these concepts belong to the toolbox of physicists. I read them quite often on our forum and their usage is sometimes a bit confusing.…

When Simple Geometry Unveils Deep Math
Introduction
It is a remarkable fact that consideration of very elementary concepts in geometry often leads quickly into deep and unexpected mathematical…

Linear Representations and Why Precision is Important in Math
First of all: What is a representation? It is the description of a mathematical object like a Lie group or a Lie algebra by its actions on another space…
Can Angles be Assigned a Dimension?
1. Some Background on Dimensional Analysis
... if you are not already familiar with it.
1.1 Dimensions
Dimensional Analysis is a way of analyzing…

Klein’s Erlangen Program: Groups Define Geometry
Klein's Erlangen program: groups and geometry
There is a very deep link between group theory and geometry. Sadly, this link is not emphasized in most…

Ramsey Theory: Foundations, Generalizations, Key Results
Ramsey theory has its origins in a very nice riddle
Consider a party of 6 people. Any two of these six will either be meeting each other for the first…

Scientific Inference: Balancing Predictive Success with Falsifiability
Bayes' Theorem: Balancing predictive success with falsifiability
Despite its murky logical pedigree, confirmation is a key part of learning.…

Is It Possible to Design an Unbreakable Cipher?
Is it possible to design an unbreakable cipher?
Do methods of encryption exist that guarantee privacy from even the most capable and highly-resourced…

The Monographic Substitution Cipher: From Julius Caesar to the KGB
A monographic substitution cipher works by replacing individual characters of plaintext with corresponding characters of ciphertext. It is perhaps the…
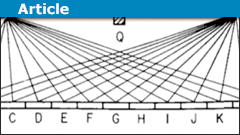
Hear the Case for Learning Complex Math
Resistance to complex math seems to never die out. I see it frequently in PF posts. Often it takes the form of challenges rather than questions. …

Things Which Can Go Wrong with Complex Numbers
At the first sight, there are many paradoxes in complex number theory. Here are some nice examples of things that don't seem to work:Example A
[itex]-1=i^2=\sqrt{-1}\cdot\sqrt{-1}=\sqrt{(-1)(-1)}=\sqrt{1}=1[/itex]Example…

Millennium Problems: Poincaré, P vs NP, Riemann
IntroductionWhat this Insight Covers
In this Insight, I will go over the background information for the Millennium Prize problems and briefly describe…
Peano Axioms: Construction of Natural Numbers and Properties
Bloch Chapter 1.2The Peano system in Bloch has a special element ##1\in \mathbb{N}##. The intuitive idea here is that ##\mathbb{N} = \{1,2,3,...\}##.…

Set-Theoretic Foundations of Numbers and Functions
Set-Theoretic Foundations of Mathematics
It is important to realize that in standard mathematics we attempt to characterize everything in terms of sets.…

Trials and Tribulations of a Physicist who Became a Math Geek
How did I go from the brink of changing my major from physics to ceramics (no more math) to the Math faculty of the Air Force Academy? How did I go from…

Teaching Math as Obvious Thinking | Make Math Click
My goal when I teach math
My #1 goal, when I teach a math class, is to convey a way of thinking about math. It's quite different from what most students…

Brachistochrone Subway Tunnel: Fastest Tunnel Shape Explained
Introduction
A subway tunnel could, in principle, operate without external energy (like electricity) if we assume zero friction everywhere. The train…

Is Zero a Natural Number?
Using: Anderson-Feil Chapter 1.1
Is zero a natural number?
This is a pretty controversial question. Many mathematicians - especially those working in foundational…

Formal Syntax and WFFs in Set Theory (Hrbacek-Jech)
Hrbacek–Jech Chapter 1.2: Formal Language and WFFs
Introduction
Hrbacek and Jech do not go into full detail about what a property is formally. This…
