Hyperbolic Definition and 336 Threads
-
D
Quasi-linear hyperbolic PDE help
I am using the book Elementary Partial Differential Equations by Berg and McGregor. However, the book neglected to discuss problems of the this form, uu_{xy}-u_xu_y=0. How do I approach this problem? Thanks.- Dustinsfl
- Thread
- Hyperbolic Pde
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
E
Graduate Distance formula in hyperbolic metric
Hi! I'm trying to derive the hyperbolic distance formula for the upper-half plane model. It is given here: http://en.wikipedia.org/wiki/Poincar%C3%A9_half-plane_model" I have the first formula, (ds)2= ... But I can't figure out how they got the distance formula below it. I understand...- elffry
- Thread
- Formula Hyperbolic Metric
- Replies: 2
- Forum: Differential Geometry
-
A
Does Geometry Influence Sound Propagation?
Homework Statement Two recording devices are set 2400 feet apart, with the device at Point A to the west of the device at point B. At a point on a line between the devices, 400 feet from point B, a small amount of explosive is detonated. The recording devices record the time the sound...- amd123
- Thread
- Hyperbolic Sound Travel
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
A
Rotation of Axis and Hyperbolic Sound Travelling Word problem?
Homework Statement 6x^2-6xy+14y^2-45=0 Two recording devices are set 2400 feet apart, with the device at Point A to the west of the device at point B. At a point on a line between the devices, 400 feet from point B, a small amount of explosive is detonated. The recording devices record...- amd123
- Thread
- Axis Hyperbolic Rotation Sound Word problem
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
L
Complex numbers, inverse trig and hyperbolic
Homework Statement edit* It says Verify the formulas in problems arcsin(z) = -iln(iz ±sqrt(1-z^2)) arccos(z) = iln(z ±sqrt(1-z^2))tanh-1z = (1/2)ln((1+z)/(1-z)) The Attempt at a Solutionyeah, my prof just threw it at us, all i have is nothing... absolutely nothing. I don't know why he does...- Liquidxlax
- Thread
- Complex Complex numbers Hyperbolic Inverse Numbers Trig
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

Graduate Symmetry Groups in Euclidean and Hyperbolic Spaces: A Comparison
Hello, how do symmetry groups in the Euclidean space differ from the symmetry groups in the hyperbolic space (in the Poincaré disk) ? I've been told that in the hyperbolic case one has at disposal a richer "vocabulary" to describe symmetries, but I don't see how, and maybe I misunderstood...- mnb96
- Thread
- Groups Hyperbolic Symmetry
- Replies: 14
- Forum: Linear and Abstract Algebra
-

Graduate Derivation of Hyperbolic Representation from Lorentz/Minkowski equations in SR
This is a carryover from a previous thread: https://www.physicsforums.com/showpost.php?p=2875138&postcount=68 Sports Fans: I am familiar with the Minkowski equations and the Lorentz transformations in one or two dimensions: A) In algebraic form (1) t2 - x2 = t'2 - x'2 (2) t' =...- stevmg
- Thread
- Derivation Hyperbolic Representation Sr
- Replies: 43
- Forum: Special and General Relativity
-
A
Integration of hyperbolic functions
Homework Statement \int cosh(2x)sinh^{2}(2x)dx Homework Equations Not sure The Attempt at a Solution This was an example problem in the book and was curious how they got to the following answer: \int cosh(2x)sinh^{2}(2x)dx = \frac{1}{2}\int sinh^{2}(2x)2cosh(2x) dx =...- Agent M27
- Thread
- Functions Hyperbolic Hyperbolic functions Integration
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
K
Graduate Understanding the Hyperbolic Distance Formula: Deriving Log QA.PB/QB.PA
I'm currently reading through Roger Penrose's book The Road to Reality and in his Hyperbolic Geometry discussion he introduces the concept of how to define the distance between two points. He defines a Conformal Representation of a Hyperbolic Space bounded by a circle and then he states there...- Kevin_Axion
- Thread
- Formula Hyperbolic
- Replies: 2
- Forum: Differential Geometry
-
X
Undergrad Why Are Hyperbolic Functions Defined Using cosh and sinh?
I have always been curious as to where the definition of cosh(x) and sinh(x) come from and how they are related to the natural exponential. I know it has something to do with Euler's formula but I don't know the details of the derivation. Could anyone shed some light on this? I haven't yet... -
A
Undergrad Natural Log Composed with Hyperbolic Tangent & this Ratio
Hello, Consider x \in (0,1) , that is x between 0 and 1. Can someone explain why the following is true: \frac{x-1}{x+1} = \tanh \left( \ln \left( \frac{x}{2} \right) \right) -

So, for tanh(ax),y = tanh(ax)x = tanh-1yx = (tanh-1y)/a
Homework Statement Now, I decided for no real reason to derive a formula for the hyperbolic tangent using only what I know about the derivative of the inverse hyperbolic tangent. However, what I have looks wrong, and I'd like to check it here. Homework Equations \frac{d...- Char. Limit
- Thread
- Hyperbolic Inverse Tangent
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
J
Hyperbolic Paraboloid: Understanding the Equation and Finding its Vertex
Homework Statement z = 2y^2 - x^2 Homework Equations The Attempt at a Solution I kind of know how to do it. z = y^2/b^2 - x^2/a^2 the first power is the axis of paraboloid. let x = k thus z = 2y^2 - k^2 and the vertex of this parabola (if x = 0 we see it is a...- jwxie
- Thread
- Hyperbolic Paraboloid
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
S
Volume of the Solid involving Hyperbolic functions
Homework Statement The area bounded by y=2 coshx, the x-axis, the y-axis, and the line x=4 is revolved about the x-axis. Find the volume of the solid generated. Homework Equations I sliced the area along the axis of revolution. That is the strip is dx. So the equation necessary is...- Strategist102
- Thread
- Functions Hyperbolic Hyperbolic functions Solid Volume
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
T
Undergrad How to Find the Solution to a Hyperbolic Graph Problem?
Hi, please find attached the problem and the short and sweet Answer. I can't understand the last step of the answer.- trojsi
- Thread
- Graph Hyperbolic
- Replies: 1
- Forum: General Math
-

Hyperbolic relationship of time and distance in relativity
Homework Statement In space-time when one "travels" a distance x from a point (within the light cone) this, in effect, comes off the time it takes. This is a hyperbolic relationship Homework Equations tau = SQRT[t2 - x2] We'll stay with one dimension (x) The Attempt at a...- stevmg
- Thread
- Hyperbolic Relationship Relativity Time
- Replies: 13
- Forum: Advanced Physics Homework Help
-
C
Graduate Lorentz boost and equivalence with 3d hyperbolic rotations
I was thinking that if i have for example a boost in the direction of x, then the boost should be equivalent to an hyperbolic rotation of the y and z axes in the other direction. I don't know if it's true or not. Then I want to know if somebody knows this result or why is false? I was...- chwie
- Thread
- 3d Boost Equivalence Hyperbolic Lorentz Lorentz boost Rotations
- Replies: 2
- Forum: Special and General Relativity
-
C
Graduate Why hyperbolic geometry in spacetime if it is flat?
This is driving me crazy. Consider a two-dimensional spacetime, with coordinates (t,x). If this is a flat spacetime, we can just imagine a regular-old two-dimensional plane. On that plane I could just as easily map a Cartesian/Euclidean coordinate system as a hyperbolic system of coordinates...- closet mathemetician
- Thread
- Flat Geometry Hyperbolic Spacetime
- Replies: 7
- Forum: Special and General Relativity
-
D
Hyperbolic Cosine curve fitting
Homework Statement I need to fit a curve using cosh to a hyperbola with a vertex of (0,0) and a point at (4,7). The scanned worksheet can be found here http://img519.imageshack.us/i/scan0001gu.jpg/" http://img192.imageshack.us/i/scan0002uz.jpg/" Homework Equations y=a cosh...- Denyven
- Thread
- Cosine Curve Curve fitting Fitting Hyperbolic
- Replies: 3
- Forum: Precalculus Mathematics Homework Help
-
U
How to find the equation for an equation from a hyperbolic graph
I need to do a project where i hang a chain from two points and find the hyperbolic function for it. The problem is, its a complete do it yourself project and i we never learned hyperbolic functions in class. That means i need to learn how to find hyperbolic fuctions from a set of data that i...- um0123
- Thread
- Graph Hyperbolic
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
I
Understanding Hyperbolic Functions
Hyperbolic functions :((( Homework Statement Question is: and Homework Equations Now from what i can recall the formula for sin(A+B) = sinAcosB+sinbcosA so same goes for hyperbolic function i suppose? sinh(2x+x) = sinh2xcoshx+cosh2xsinx (2sinhxcoshx)coshx +...- ibysaiyan
- Thread
- Functions Hyperbolic Hyperbolic functions
- Replies: 3
- Forum: Precalculus Mathematics Homework Help
-
B
Differentiating Hyperbolic Functions
1. Differentiate cosh(x) using first principles 2. cosh(x) = (e^x+e^-x)/2 From previous exercises, I know the answer will be sinh(x)= (e^x-e^-x)/2 but I cannot get to the answer. I seem to be left with the equation: lim h ---> 0 (e^2x*e^2h +1-e^h*2e^x +e^h)/(2h*e^x*e^h) But when...- BoT
- Thread
- Differentiating Functions Hyperbolic Hyperbolic functions
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
C
Graduate Identifying tiles in hyperbolic space?
"Identifying" tiles in hyperbolic space? So I have a software project I've been working on on and off that involves the hyperbolic plane. There is something I am stuck on: So let's say I have filled the hyperbolic plane with one of the tilings of regular n-gons. I now would like to "label"...- Coin
- Thread
- Hyperbolic Space
- Replies: 3
- Forum: Differential Geometry
-
P
Undergrad Hyperbolic Geometry: Euclidean v 4D in 3D Space
Greetings PF, I do very much love lurking these forums for countless hours of leisure brain twisting. Infinite thanks for that. A very simple question for you all. I believe the answer is 'true', however, I'm not formally educated in mathematics, so I feel a bit like I'm grabbing at...- Praxisseiz
- Thread
- Geometry Hyperbolic
- Replies: 2
- Forum: Differential Geometry
-
D
Proving Existence of a Triangle with Defect > 14 Degrees in Hyperbolic Geometry
Homework Statement How to show that there exists a triangle whose defect is greater than 14 degrees Homework Equations The Attempt at a Solution No idea what to do here... something about the angle of parallelism- dancergirlie
- Thread
- Geometry Hyperbolic
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
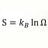
Undergrad Hyperbolic trigonometric functions in terms of e ?
cosh x= e^x+e^-x/2 sinh x= e^x-e^-x/2 Can someone explain why the hyperbolic trigonometric functions are defined in terms of the natural exponential function, e^x ?- morrobay
- Thread
- Functions Hyperbolic Terms Trigonometric Trigonometric functions
- Replies: 6
- Forum: General Math
-
C
Limit of e^(2x) / sinh(2x) as x approaches infinity
Homework Statement Find the limit of e^(2x) / sinh(2x), as x approaches infinity. Homework Equations The Attempt at a Solution Changed equation to e^(2x) / [(e^(2x) - e^(-2x)) / 2]. Based of the sinh identity. found limit of e^(2x) = ∞ ... e^(-2x) = 0 ... 2 = 2...- ccha
- Thread
- Hyperbolic Limit
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Undergrad Origin of hyperbolic functions
I read the wiki on hyperbolic functions but i don't really understand. I also plotted cosht,sinht on wolfram it made sideways v lying on the x axis. Can anyone explain why people made hyperbolic functions. I still don't really understand what it means apart from cosht being the x coordinate...- SpartanG345
- Thread
- Functions Hyperbolic Hyperbolic functions Origin
- Replies: 4
- Forum: General Math
-
A
Graduate OUT Hyperbolic Motions | 65 Characters
Hi everybody I've been lately a little bit concerned over the hyperbolic motions that have the following equations in (ct,x)-space: \frac{x^2}{(c^2/a)^2}-\frac{(ct)^2}{(c^2/a)^2}=1. We know that events horizons are the lines that form a 45-degree angle by both ct- and x-axis. So what...- Altabeh
- Thread
- Hyperbolic
- Replies: 5
- Forum: Special and General Relativity
-
A
Graduate Identifying the Type of PDE and Methods for Solving It
Hello dear friends, I have this PDE Can anyone help me in finding what type PDE is it. So that I can try to solve this . As per my knowledge, I think this is second order and Nonlinear Is my guess is correct? Is it parabolic or hyperbolic, or is Elliptic and what method can...- alokgautam
- Thread
- Hyperbolic
- Replies: 7
- Forum: Differential Equations
-
G
Need Short Easy Primer on Hyperbolic Functions
Hello All, Am studying GR using a text by Hartle. From time to time need a better intuitive understanding of hyperbolic functions than I currently have. Never learned them for my physics undergrad. Any short sweet highly understandable primer, etc, that anyone knows of (preferably free of...- glamotte7
- Thread
- Functions Hyperbolic Hyperbolic functions Short
- Replies: 3
- Forum: Science and Math Textbooks
-
B
Graduate Why vacuum Einstein equations are hyperbolic equations?
Hello friends, I am now interested in Einstein scalar field equations with a very little knowledge about Physics. I would like to ask why vacuum Einstein equations are hyperbolic equations? As far as I know that for 3+1-dimensional manifold V, we can convert the vacuum Einstein equations as a...- bookworm_vn
- Thread
- Einstein Hyperbolic Vacuum
- Replies: 5
- Forum: Special and General Relativity
-
I
Undergrad One question about Parabolic and Hyperbolic trajectory.
In the Parabolic and Hyperbolic trajectory.Is the sun in the focus point of parabola and hyperbola?- IPhO' 2008
- Thread
- Hyperbolic Trajectory
- Replies: 3
- Forum: Astronomy and Astrophysics
-
I
Undergrad Orbital energy of ellipse and hyperbolic trajectory
Please tell me how to find the orbital energy of ellipse and hyperbolic trajectory. Thank you.- IPhO' 2008
- Thread
- Ellipse Energy Hyperbolic Orbital Trajectory
- Replies: 2
- Forum: Astronomy and Astrophysics
-
Y
Solving equation with natural log with inverse hyperbolic
Homework Statement Solve ln(sinh-1(x)) = 1 (Just give the formula for x, no calculator is necessary) sinh-1(x) = asinh Homework Equations The Attempt at a Solution When I did this, I knew sinh-1(x) = ln(x + sqrt.(x^2 +1), but the equation would look like ln(ln(x +...- yojo95
- Thread
- Hyperbolic Inverse Log Natural Natural log
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
S
Find inverse hyperbolic function
Homework Statement find f-1(t) and compute f-1(0) where f(t) = sinh(t)Homework Equations sinh(t)=( et- e-t)/2The Attempt at a Solution t= (ey- e-y)/2 ln2t = y - - y y = (ln2t)/2 but wikipedia says http://upload.wikimedia.org/math/8/e/d/8edd21edb4cd413e462fe82ef4ac249b.png" what silly...- synergix
- Thread
- Function Hyperbolic Inverse
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
B
Using the inverse hyperbolic tangent function to solve ODE
Homework Statement Hi all. I have to solve the differential equation \frac{dv}{dt} = g(1 - \frac{\rho}{g}v^2). The Attempt at a Solution Apparently the solution should involve the inverse hyperbolic tangent function - with the equation in this form it should just be separable, correct...- bitrex
- Thread
- Function Hyperbolic Inverse Ode Tangent
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
W
Help with hyperbolic functions: cosh(arcsinh(x/2))=?
Homework Statement I need to solve: 1/4tanh(θ) + c Homework Equations x=2sinh(θ) θ = arcsinh(x/2) The Attempt at a Solution I worked out that since tanh(θ) = sin(θ)/cosh(θ) then 1/4tanh(θ) + c = x/8cosh(θ) + c But i don't know how to work out cosh(θ) or cosh(arcsinh(x/2))...- wshfulthinker
- Thread
- Functions Hyperbolic Hyperbolic functions
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
S
How do you find sinhx and coshx when tanhx = 12/13?
Homework Statement find all other hyperbolic function at x for tanhx=12/13 Homework Equations tanhx = sinhx/coshx cothx=1/tanhx etc... The Attempt at a Solution the only thing i got is cothx=13/12 all i need to know is how to find sinhx and i will be fine.- Slimsta
- Thread
- Functions Hyperbolic Hyperbolic functions
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
J
Graduate Area of a hyperbolic paraboloid contained within a cylinder
I've posted on this before and have now realized I was doing it completely wrong before but's still bugging me. I have to find the area of the hyperbolic paraboloid z=xy contained within the cylinder x^{2}+y^{2}=1. I've parametrized x^{2}+y^{2}=1 into polar coordinates to give that...- Juggler123
- Thread
- Area Cylinder Hyperbolic Paraboloid
- Replies: 1
- Forum: Calculus
-
J
Graduate Finding the Area of a Hyperbolic Paraboloid
I need to find the area of the hyperbolic paraboloid z=xy contained within the cylinder x^2+y^2=1. I know I need to take a double integral but am having real difficulty finding the correct limits, so far I've got that; \int dx\int dy With the x limits being 1 and -1 and the upper y limit...- Juggler123
- Thread
- Area Hyperbolic Paraboloid
- Replies: 2
- Forum: Calculus
-
S
Hyperbolic Functions: Graphs - question
Homework Statement $\displaystyle \Large y = \ln (x + \sqrt{x^2 - 1})$ Homework Equations The Attempt at a Solution i used my graphing calc.. but that's not the point. how do i do this question? i mean, how do i find the graph of that function?- Slimsta
- Thread
- Functions Graphs Hyperbolic Hyperbolic functions
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
P
Hyperbolic Functions cosh(2-3i)
Homework Statement Find the real part, the imaginary part, and the absolute value of: cosh(2-3i) Homework Equations The Attempt at a Solution I know how to write this using exponentials, but when I looked up the answer the book expanded cosh(2-3i) to cosh 2 cos 3 − i sinh 2...- phrygian
- Thread
- Functions Hyperbolic Hyperbolic functions
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
U
Find Steepest Climb of this Hyperbolic Paraboloid
Delete please.- UziStuNNa
- Thread
- Hyperbolic Paraboloid
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
O
Impulsive delta v hyperbolic and elliptical orbit
Homework Statement On July 1, 2004, the Cassini spacecraft approached Saturn with hyperbolic excess velocity 5.5 km/s to swing by the planet at the closest approach distance rp = 80,680 km. Compute the impulsive ΔV required for a maneuver performed at the closest approach to Saturn to...- orbitsnerd
- Thread
- Delta Delta v Elliptical orbit Hyperbolic Orbit
- Replies: 3
- Forum: Advanced Physics Homework Help
-
K
Graduate 2nd order linear hyperbolic PDE?
uxx - x2 uyy = 0 (assume x>0) Is there any systematic method (e.g. change of variables) to solve this hyperbolic equation? dy/dx = [B + sqrt(B2 - AC)]/A => dy/dx = x => 2y -x2 = c dy/dx = [B - sqrt(B2 - AC)]/A => dy/dx = -x => 2y + x2 = k So the characteristic curves are 2y -x2 =...- kingwinner
- Thread
- 2nd order Hyperbolic Linear Pde
- Replies: 3
- Forum: Differential Equations
-
N
Hyperbolic Functions with Constants k and m: dy/dx Formula
y=km(ln(cosh(gt/km)^(1/2))) constants k and m dy/dx=gtanh((gt/km)^(1/2))/(2(gt/km)^(1/2))...?- nameVoid
- Thread
- Functions Hyperbolic Hyperbolic functions
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
N
Hyperbolic Functions and Tangent Line Slope 2 at y=sinhx
Find the points on the graph of y=sinhx at which the tangent line has slope 2 dy/dx=coshx=2 (e^x+e^(-x))=4 x-x=ln4- nameVoid
- Thread
- Functions Hyperbolic Hyperbolic functions
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
N
The relationship between hyperbolic and circular functions
Hello! A book on calculus was introducing hyperbolic functions and pointed out that the identities such as cosh x and sinh x, etc. for hyperbolic functions were analogous to cos x and sin x for circular functions. I tried finding some internet sources explaining why this is so, but they tend to...- nobahar
- Thread
- Circular Functions Hyperbolic Relationship
- Replies: 3
- Forum: Precalculus Mathematics Homework Help
-
B
Undergrad The hyperbolic tangent function and physics
Kind of an odd question, but here goes: can anyone offer any examples of physical systems that include the use of the hyperbolic tangent function in their mathematical solution?- bitrex
- Thread
- Function Hyperbolic Physics Tangent
- Replies: 7
- Forum: Beyond the Standard Models