Physics, Math and Science Articles
Independent Research: Thinking Outside The Box Versus Knowing What’s In The Box
/1 Comment/in Physics Articles/by fresh_42In Memory of Dr. Thomas J. LeCompte (1964-2025), Detector Designer and Champion of Education and Science. Prologue Someone who shows interest in science is initially a welcome development. So are fresh ideas from unexpected quarters. In contrast, there is a scientific community that is meticulously organized down to the last detail, allowing little to no…
Trending Articles
 What Planck Length Is and It’s Common Misconceptions 348 views | by Alex Klotz | posted on September 9, 2015
What Planck Length Is and It’s Common Misconceptions 348 views | by Alex Klotz | posted on September 9, 2015 Can We See an Atom? 273 views | by Alex Klotz | posted on September 28, 2015
Can We See an Atom? 273 views | by Alex Klotz | posted on September 28, 2015 What Is a Tensor? The mathematical point of view. 123 views | by fresh_42 | posted on June 18, 2017
What Is a Tensor? The mathematical point of view. 123 views | by fresh_42 | posted on June 18, 2017 How to Measure Internal Resistance of a Battery 115 views | by Neil Parker | posted on February 14, 2023
How to Measure Internal Resistance of a Battery 115 views | by Neil Parker | posted on February 14, 2023 Quantum Physics via Quantum Tomography: A New Approach to Quantum Mechanics 107 views | by Arnold Neumaier | posted on January 8, 2022
Quantum Physics via Quantum Tomography: A New Approach to Quantum Mechanics 107 views | by Arnold Neumaier | posted on January 8, 2022
Recent Entries
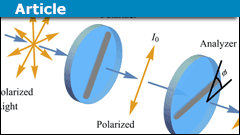
Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality per Quantum Information Theory
/
0 Comments
In her YouTube video Bell's Theorem Experiments on Entangled Photons, Dr. Fugate shows how polarization-entangled photons violate Bell's inequality. In…

Relativator (Circular Slide-Rule) – Simulated with Desmos
The Relativator (revisited)
This is an update of my 2006 post (reconstructed in 2014) Relativator: The circular slide-rule for physicists.
This is a…
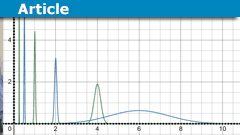
What Exactly is Dirac’s Delta Function?
Introduction: "Convenient Notation"In Dirac's Principles of Quantum Mechanics published in 1930 he introduced a "convenient notation" he referred …
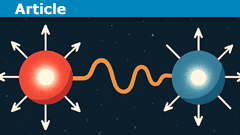
Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
Towards the end of the first lecture for the Qiskit Global Summer School 2025, Foundations of Quantum Mechanics, Olivia Lanes (Global Lead, Content and…

Fixing Things Which Can Go Wrong With Complex Numbers
Abstract
This article will build on the hints about treating the complex numbers as a branched surface, briefly described and pictured in section 4.2…

Fermat’s Last Theorem
Abstract
Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states…
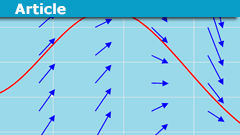
Why Vector Spaces Explain The World: A Historical Perspective
The Concept
A vector space is an additively written abelian group together with a field that operates on it.
Vector spaces are often described as a set…

Groups, The Path from a Simple Concept to Mysterious Results
Introduction
The concept of a group is as simple as it gets: a set with a binary operation like addition and a couple of natural laws like the requirement…
A Possible AI Modern Video Codec
Introduction
Modern Video codecs are all based on similar principles. Recently, these have been complemented by AI techniques, such as super-resolution,…
Beyond the Tidal Bulge
Overview
That there is no tidal bulge is the key premise of this article. Upper-level oceanography undergraduates and above know this. Yet the tidal bulge…

The Many Faces of Topology
Abstract
Topology as a branch of mathematics is a bracket that encompasses many different parts of mathematics. It is sometimes even difficult to see…
Brownian Motions and Quantifying Randomness in Physical Systems
Stochastic calculus has come a long way since Robert Brown described the motion of pollen through a microscope in 1827. It's now a key player in data science,…
PBS Video Comment: “What If Physics IS NOT Describing Reality”
PBS Space Time produces some very good videos on the foundations of quantum mechanics (QM), so let me comment on their video What If Physics IS NOT Describing…
Aspects Behind the Concept of Dimension in Various Fields
Abstract
It took until the last century for physicists and mathematicians in the Netherlands to question the Euclidean concept of dimension as length,…

Views On Complex Numbers
Abstract
Why do we need yet another article about complex numbers? This is a valid question and I have asked it myself. I could mention that I wanted…

Addition of Velocities (Velocity Composition) in Special Relativity
The "Addition of Velocities" formula (more correctly, the "Composition of Velocities" formula) in Special Relativity[tex]\frac{v_{AC}}{c}=\frac{ \frac{v_{AB}}{c}+\frac{v_{BC}}{c}…

Schrödinger’s Cat and the Qbit
The concept of quantum superposition (or superposition for short) is very counterintuitive, as Schr##\ddot{\text{o}}##dinger noted in 1935 writing [1],…

The Slinky Drop Experiment Analysed
The slinky drop is a rather simple experiment. In its most basic form, it requires only a popular toy for children, a stable hand, and a keen eye.…

Spatial Curvature in Cosmological Models
Standard cosmological models are classified by spatial curvature into three broad types: open, flat, and closed universes. These correspond to negative,…

All About the Einstein Field Equations
Definition/Summary
The Einstein Field Equations (EFE) are a set of ten interrelated differential equations that form the core of Einstein's general theory…
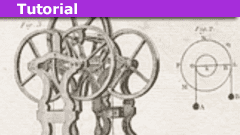
How to Solve a Multi-Atwood Machine Assembly
IntroductionThe figure on the right shows a "double-double" Atwood machine with three ideal pulleys and four masses. All pulleys are released from…

The Lambert W Function in Finance
Preamble
The classical mathematician practically by instinct views the continuous process as the "real" process, and the discrete process as an approximation…

Why Division by Zero is a Bad Idea
A division by zero is primarily an algebraic question. The reasoning therefore follows the indirect pattern of most algebraic proofs:
What if it was allowed?
Then…

Digital Filtering and Exact Reconstruction of Digital Audio
Introduction
This elaborates some of the claims in my insights article on digital audio.
The Sinc Function
The first link in my insights article has…

Introduction to Modern Digital Audio Concepts
IntroductionFirst, we need some background in Digital Signals. This can be mathematically quite advanced, but since I would like this…
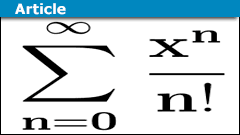
Series in Mathematics: From Zeno to Quantum Theory
Introduction
Series play a decisive role in many branches of mathematics. They accompanied mathematical developments from Zeno of Elea (##5##-th century…
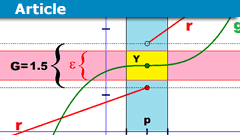
Epsilontic – Limits and Continuity
Abstract
I remember that I had some difficulties moving from school mathematics to university mathematics. From what I read on PF through the years, I…

The Poor Man’s Milli-Ohm Meter
Introduction
In a previous article on measuring battery internal resistance, a simple technique for low-resistance measurement was outlined. In this article,…

Differential Equation Systems and Nature
Abstract
"Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…

Beginners Guide to Precalculus, Calculus and Infinitesimals
Introduction
I am convinced students learn Calculus far too late. In my view, there has never been a good reason for this.In the US, they go through…

How to Apply Newton’s Second Law to Variable Mass Systems
Introduction
The applicability of Newton's second law in the oft-quoted "general form" $$\begin{align}\frac{d\mathbf{P}}{dt}=\mathbf{F}_{\text{ext}}\end{align}$$…

What Are Numbers?
Introduction
When doing mathematics, we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive. Going…

Introduction to the World of Algebras
Abstract
Richard Pierce describes the intention of his book [2] about associative algebras as his attempt to prove that there is algebra after Galois…

Why ChatGPT AI Is Not Reliable
I'll start with the simple fact: ChatGPT is not a reliable answerer to questions.To try to explain why from scratch would be a heavy lift, but fortunately,…

What Are Infinitesimals – Simple Version
Introduction
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…

How Quantum Information Theory Solves “the only mystery” of Quantum Mechanics
In Chapter 37 of "The Feynman Lectures on Physics Volume 1," Richard Feynman famously wrote that the mystery of wave-particle duality in the double-slit…

What Are Infinitesimals – Advanced Version
Introduction
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…

When Pro Scientists Explain Using Pop Science
Abstract
There is so much to say about the many endeavors by professional scientists to explain to us the world. The list is long: Carl Sagan, Harald…

The Art of Integration
Abstract
My school teacher used to say
"Everybody can differentiate, but it takes an artist to integrate."
The mathematical reason behind this phrase…

A Lesson In Teaching Physics: You Can’t Give It Away
A central principle of Physics Forums regarding homework help is not to provide solutions on demand but to guide students along a path to the answer. The…

An Overview of Complex Differentiation and Integration
Abstract
I want to shed some light on complex analysis without getting all the technical details in the way which are necessary for the precise treatments…
How to Measure Internal Resistance of a Battery
Introduction
A commonly encountered school-level Physics practical is the determination of the internal resistance of a battery - typically an AA or D…

When Lie Groups Became Physics
Abstract
We explain by simple examples (one-parameter Lie groups), partly in the original language, and along the historical papers of Sophus Lie, Abraham…

Why There Are Maximum Mass Limits for Compact Objects
In this article, we will look at why there are maximum mass limits for objects that are supported against gravity by degeneracy pressure instead of kinetic…

Oppenheimer-Snyder Model of Gravitational Collapse: Implications
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsIn the last article in this series, we finished up with a metric for the Oppenheimer-Snyder…

What Are Tensors and Why Are They Used in Relativity?
If you try learning general relativity, and sometimes special relativity, on your own, you will undoubtedly run into tensors. This article will outline…

Oppenheimer-Snyder Model of Gravitational Collapse: Mathematical Details
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsIn a previous article, I described in general terms the model of gravitational…

When Discussing the Twin Paradox: Read This First
This article is intended for anyone who wants to start a thread here at Physics Forums on the twin paradox. There are already many, many threads here on…

The Oppenheimer-Snyder Model of Gravitational Collapse: An Overview
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsMost people who have spent any time at all studying GR are familiar with the…

Subtleties Overlooked in Friction Questions: Object Slides Down Ramp
Problem statement (simplified)
An object slides down a ramp at angle θ to encounter level ground. Both surfaces have kinetic friction: μ' on the ramp,…
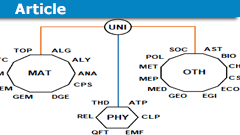
Classification of Mathematics by 42 Branches
I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what has…

Reduction of Order For Recursions
This is not meant as a full introduction to recursion relations but it should suffice for just about any level of the student.Most of us remember recursion…

Counting to p-adic Calculus: All Number Systems That We Have
An entire book could easily be written about the history of numbers from ancient Babylon and India, over Abu Dscha'far Muhammad ibn Musa al-Chwarizmi (##\sim…

Évariste Galois and His Theory
* Oct. 25th, 1811 † May 31st, 1832
... or why squaring the circle is doomed.
Galois died in a duel at the age of twenty. Yet, he gave…
Yardsticks to Metric Tensor Fields
I asked myself why different scientists understand the same thing seemingly differently, especially the concept of a metric tensor. If we ask a topologist,…

Programming an ATmega8A using Arduino
If you are interested in programming and electronics, you probably do not need an introduction to Arduino. If you want to make your Arduino projects permanent,…

P vs. NP and what is a Turing Machine (TM)?
P or NP
This article deals with the complexity of calculations and in particular the meaning of
##P\stackrel{?}{\neq}NP##
Before we explain what P and…

Quantum Computing for Beginners
This article provides an accessible introduction to quantum computing, a cutting-edge technology that processes certain types of information much faster…
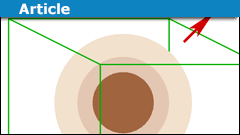
A Physics Misconception with Gauss’ Law
Introduction
It is relatively common to see the following type of argument:
The surface area is ##A## and the enclosed charge is ##Q##. The electric…
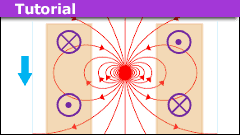
How to Model a Magnet Falling Through a Conducting Pipe
Introduction
In an earlier article, we examined a magnet falling through a solenoid. We argued that the point dipole model can account for the basic features…
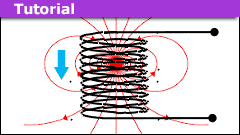
How to Model a Magnet Falling Through a Solenoid
Introduction
Modeling a magnet realistically is a task best done numerically. Even the simplified model of two separated disks with uniform surface…

How Can We Jump When the Ground Does No Work?
It is relatively common on Physics Forums to see arguments that are effectively similar to the following:
When we jump off the ground, the ground does…
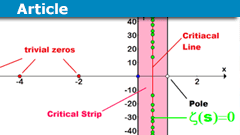
The History and Importance of the Riemann Hypothesis
Riemann Hypothesis History
The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…
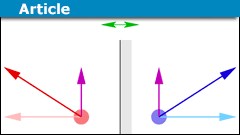
Symmetry Arguments and the Infinite Wire with a Current
Many people reading this will be familiar with symmetry arguments related to the use of Gauss law. Finding the electric field around a spherically symmetric…

Parallel Programming on a CPU with AVX-512
This article is the second of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different…

Parallel Programming on an NVIDIA GPU
This article is the first of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different…

A Novel Technique of Calculating Unit Hypercube Integrals
Introduction
In this insight article, we will build all the machinery necessary to evaluate unit hypercube integrals by a novel technique. We will first…
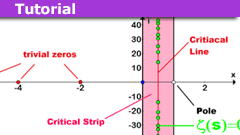
The Extended Riemann Hypothesis and Ramanujan’s Sum
Riemann Hypothesis and Ramanujan's Sum ExplanationRH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line.
ERH: All…
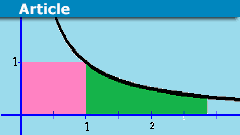
The Amazing Relationship Between Integration And Euler’s Number
We use integration to measure lengths, areas, or volumes. This is a geometrical interpretation, but we want to examine an analytical interpretation that…

Superdeterminism and the Mermin Device
Superdeterminism as a way to resolve the mystery of quantum entanglement is generally not taken seriously in the foundations community, as explained in…
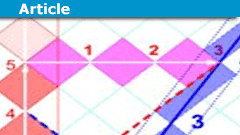
Relativity on Rotated Graph Paper (a graphical motivation)
(based on https://www.physicsforums.com/threads/teaching-sr-without-simultaneity.1011051/post-6588952 and https://physics.stackexchange.com/a/689291/148184…

Probabilistic Factors Involved in Disease and Virus Testing
Introduction
This Insight looks at the various probabilistic factors and related terminology involved in disease and virus testing.As we all know,…

Quantum Physics via Quantum Tomography: A New Approach to Quantum Mechanics
This Insight article presents the main features of a conceptual foundation of quantum physics with the same characteristic features as classical physics…

A Trick to Memorizing Trig Special Angle Values Table
In calculus classes when you are asked to evaluate a trig function at a specific angle, it's 99.9% of the time at one of the so-called special angles we…

How to Setup a Raspberry Pi Cluster
INTRODUCTION
As a long-time computer programmer and almost as long a High-Performance Computer (HPC) user, I didn't know anything about how these machines…
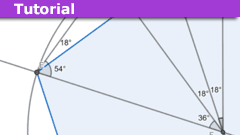
An Introduction to Theorema Primum
Introduction
Whilst no doubt most frequenters of "Physics Forums" will be familiar with Nicolaus Copernicus as the scientist who advanced the (at the…

Python’s Sympy Module and the Cayley-Hamilton Theorem
Two of my favorite areas of study are linear algebra and computer programming. In this article I combine these areas by using Python to confirm that a…

Geodesic Congruences in FRW, Schwarzschild and Kerr Spacetimes
Introduction
The theory of geodesic congruences is extensively covered in many textbooks (see References); what follows in the introduction is a brief…

Physical Applications of the “Tan Rule”
Introduction
Every secondary school student who has encountered trigonometry in his/her Math syllabus will most likely have come across the sine, cosine,…

Corrections to MIT Open Courseware: Systems of Varying Mass
Corrections to
MIT Open Courseware 8-01sc classical mechanics,
fall 2016
Applying Newton's Laws to systems of Varying Mass
PDF Course Link
My concerns…

How Quantum Information Theorists Revealed the Relativity Principle at the Foundation of Quantum Mechanics
This Insight is a condensed version of No Preferred Reference Frame at the Foundation of Quantum Mechanics. Reference numbers here correspond to that paper.…

Investigating Some Euler Sums
So, why only odd powers? Mostly because the even powers were solved by Leonard Euler in the 18th century. Since the “mathematical toolbox” at that…
Quaternions in Projectile Motion
Introduction
In a previous Physics Forums article entitled “How to Master Projectile Motion Without Quadratics”, PF user @kuruman brought to our…

Quantum Mechanics and the Famous Double-slit Experiment
Double-slit Key PointsQuantum mechanics is known for its strangeness, including phenomena like wave–particle duality, which allows particles to…

When Science is Not Enough: Legal and Health Implications of Questions
There are often questions on Physics Forums related to building machines or structures that are left unanswered because of this guideline (found in the…

The LCEVC Coding Standard and 8K Television
Introduction
First, for background, here is an overview of the most common video compression standard in use today, H264: https://www.maketecheasier.com/how-video-compression-works/H265…
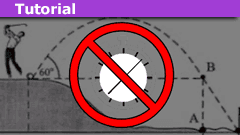
How to Solve Projectile Motion Problems in One or Two Lines
Introduction
We show how one can solve most if not all, introductory-level projectile motion problems in one or maybe two lines. To this end, we forgo…

10 Math Things We All Learnt Wrong At School
Some of these could even lead to heavy debates within the scientific community, so maybe I should say: from my point of view. So before you get excited…

Computing the Riemann Zeta Function Using Fourier Series
Euler's amazing identity
The mathematician Leonard Euler developed some surprising mathematical formulas involving the number ##\pi##. The most famous…

Tolman Law in a Nutshell
The Tolman law describes how the temperature in a fixed gravitational field depends on the position (see https://arxiv.org/abs/1803.04106 for a pedagogic…

Maximizing Horizontal Range of a Projectile
Introduction
A recent homework problem that appeared in the forums was concerned with maximizing the horizontal range of a projectile subject to the launch…

A Numerical Electromagnetic Solver Using Duality
In the previous insights article (How to Use Duality in Computational Electromagnetic Problems), I covered some uniqueness theorems for the Riemann-Silberstein…

The Electric Field Seen by an Observer: A Relativistic Calculation with Tensors
This Insight was inspired by the discussion in "electric field seen by an observer in motion", which tries to understand the relation between two expressions:…
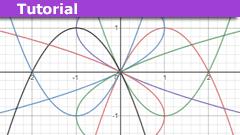
Valentine’s Reflections: Mathematical Matters of the Heart
Introduction
Being a somewhat geeky Maths 'nerd', I spent days leading up to Valentine's Day trying to find a Maths function appropriate to the day. In…
Posterior Predictive Distributions in Bayesian Statistics
Confessions of a moderate Bayesian, part 4
Bayesian statistics by and for non-statisticiansRead part 1: How to Get Started with Bayesian StatisticsRead…

How to Use Duality in Computational Electromagnetic Problems
Some weeks ago I happened across a post that caught my eye. Dale asked a question about the number of photons in an electromagnetic field. His question…
Ambiguous Case (SSA): When Triangles Are Impossible Explained
What is the ambiguous case?
In U.S. high schools, students are often introduced to geometric proofs for the first time. A common task is to use a small…

Equations of Motion Revisited
Introduction
In any school Physics course, the Newtonian equations of motion are very much a 'stock' item. Students learn the equations and are given…

How Bayesian Inference Works in the Context of Science
Confessions of a moderate Bayesian part 3
Read part 1: How to Get Started with Bayesian Statistics
Read part 2: Frequentist Probability vs Bayesian ProbabilityBayesian…
Exploring Frequentist Probability vs Bayesian Probability
Confessions of a moderate Bayesian, part 2
Read Part 1: Confessions of a moderate Bayesian, part 1Bayesian statistics by and for non-statisticianshttps://www.cafepress.com/physicsforums.13280237
Background
One…

