Science and Math Tutorials

Here contain the expert tutorials for all science and math disciplines.  This is a master list. Tutorials are technical and focus on one narrow skill. It’s more like a how-to than a guide.

einstein field equations

All About the Einstein Field Equations

/
0 Comments
Definition/Summary The Einstein Field Equations (EFE) are a set of ten interrelated differential equations that form the core of Einstein's general theory…
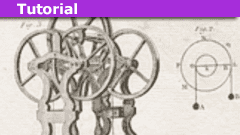
Multi-Atwood Machine Assembly

How to Solve a Multi-Atwood Machine Assembly

/
2 Comments
IntroductionThe figure on the right shows a "double-double" Atwood machine with three ideal pulleys and four masses.  All pulleys are released from…
Variable Mass Systems

How to Apply Newton’s Second Law to Variable Mass Systems

/
0 Comments
Introduction The applicability of Newton's second law in the oft-quoted "general form"  $$\begin{align}\frac{d\mathbf{P}}{dt}=\mathbf{F}_{\text{ext}}\end{align}$$…
chatgpt-reliable

Why ChatGPT AI Is Not Reliable

/
138 Comments
I'll start with the simple fact: ChatGPT is not a reliable answerer to questions.To try to explain why from scratch would be a heavy lift, but fortunately,…
art of integration

The Art of Integration

/
0 Comments
Abstract My school teacher used to say "Everybody can differentiate, but it takes an artist to integrate." The mathematical reason behind this phrase…
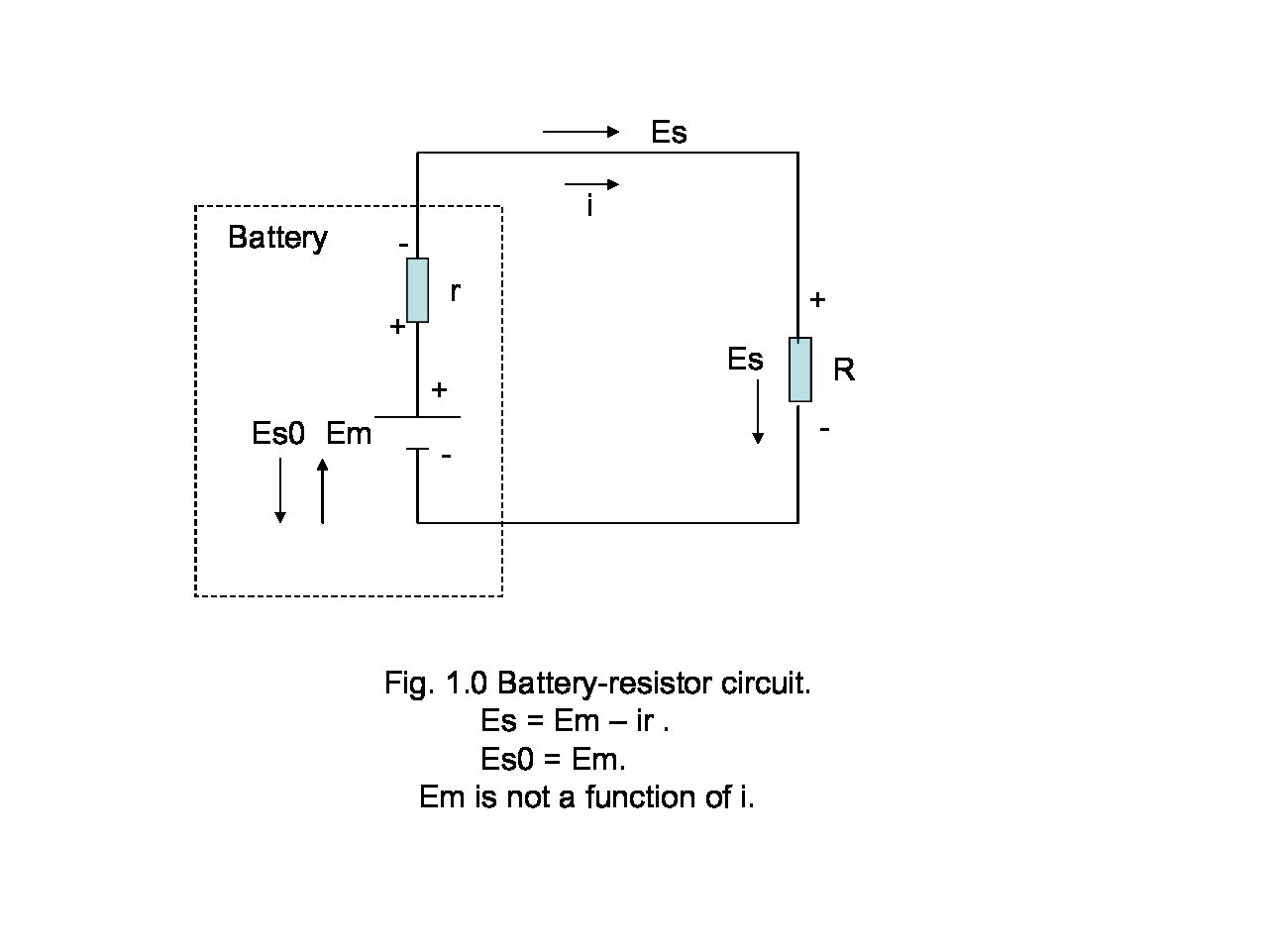
Measure Internal Resistance of Battery

How to Measure Internal Resistance of a Battery

/
0 Comments
Introduction A commonly encountered school-level Physics practical is the determination of the internal resistance of a battery - typically an AA or D…
object slide down ramp physics

Subtleties Overlooked in Friction Questions: Object Slides Down Ramp

/
0 Comments
Problem statement (simplified) An object slides down a ramp at angle θ to encounter level ground. Both surfaces have kinetic friction: μ' on the ramp,…
recursion

Reduction of Order For Recursions

/
0 Comments
This is not meant as a full introduction to recursion relations but it should suffice for just about any level of the student.Most of us remember recursion…
pvsnp

P vs. NP and what is a Turing Machine (TM)?

/
1 Comment
P or NP This article deals with the complexity of calculations and in particular the meaning of ##P\stackrel{?}{\neq}NP## Before we explain what P and…
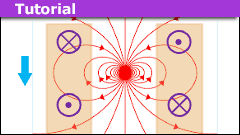
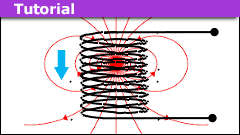
model magnet

How to Model a Magnet Falling Through a Conducting Pipe

/
7 Comments
Introduction In an earlier article, we examined a magnet falling through a solenoid. We argued that the point dipole model can account for the basic features…
model magnet

How to Model a Magnet Falling Through a Solenoid

/
11 Comments
Introduction Modeling a magnet realistically is a task best done numerically.  Even the simplified model of two separated disks with uniform surface…
cpu programming

Parallel Programming on a CPU with AVX-512

/
1 Comment
This article is the second of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different…
programming gpu

Parallel Programming on an NVIDIA GPU

/
1 Comment
This article is the first of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different…
hypercube integral

A Novel Technique of Calculating Unit Hypercube Integrals

/
1 Comment
Introduction In this insight article, we will build all the machinery necessary to evaluate unit hypercube integrals by a novel technique. We will first…
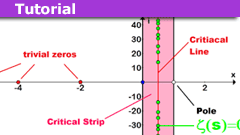
Riemann Hypothesis

The Extended Riemann Hypothesis and Ramanujan’s Sum

/
2 Comments
Riemann Hypothesis and Ramanujan's Sum ExplanationRH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line. ERH: All…
trig special functions

A Trick to Memorizing Trig Special Angle Values Table

/
3 Comments
In calculus classes when you are asked to evaluate a trig function at a specific angle, it's 99.9% of the time at one of the so-called special angles we…
setup raspberry pi cluster

How to Setup a Raspberry Pi Cluster

/
9 Comments
INTRODUCTION As a long-time computer programmer and almost as long a High-Performance Computer (HPC) user, I didn't know anything about how these machines…
Theorema Primum tutorial

An Introduction to Theorema Primum

/
0 Comments
Introduction Whilst no doubt most frequenters of "Physics Forums" will be familiar with Nicolaus Copernicus as the scientist who advanced the (at the…
python sympy module

Python’s Sympy Module and the Cayley-Hamilton Theorem

/
0 Comments
Two of my favorite areas of study are linear algebra and computer programming. In this article I combine these areas by using Python to confirm that a…
Kerr Spacetime

Geodesic Congruences in FRW, Schwarzschild and Kerr Spacetimes

/
5 Comments
Introduction The theory of geodesic congruences is extensively covered in many textbooks (see References); what follows in the introduction is a brief…
tan rule

Physical Applications of the “Tan Rule”

/
0 Comments
Introduction Every secondary school student who has encountered trigonometry in his/her Math syllabus will most likely have come across the sine, cosine,…
MIT course corrections

Corrections to MIT Open Courseware: Systems of Varying Mass

/
1 Comment
Corrections to MIT Open Courseware 8-01sc classical mechanics, fall 2016 Applying Newton's Laws to systems of Varying Mass PDF Course Link My concerns…
euler sums

Investigating Some Euler Sums

/
0 Comments
So, why only odd powers? Mostly because the even powers were solved by Leonard Euler in the 18th century. Since the “mathematical toolbox” at that…
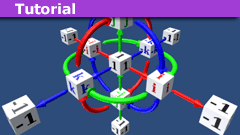
Quaternions in Projectile Motion

Quaternions in Projectile Motion

/
2 Comments
Introduction In a previous Physics Forums article entitled “How to Master Projectile Motion Without Quadratics”, PF user @kuruman brought to our…
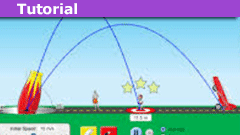
solving projectile motion

How to Solve Projectile Motion Problems in One or Two Lines

/
1 Comment
Introduction We show how one can solve most if not all, introductory-level projectile motion problems in one or maybe two lines. To this end, we forgo…
Fourier Series Riemann Zeta Function

Computing the Riemann Zeta Function Using Fourier Series

/
5 Comments
Euler's amazing identity The mathematician Leonard Euler developed some surprising mathematical formulas involving the number ##\pi##. The most famous…
physics cannonball projectile

Maximizing Horizontal Range of a Projectile

/
7 Comments
Introduction A recent homework problem that appeared in the forums was concerned with maximizing the horizontal range of a projectile subject to the launch…
electromagnetic computations duality

A Numerical Electromagnetic Solver Using Duality

/
0 Comments
In the previous insights article (How to Use Duality in Computational Electromagnetic Problems), I covered some uniqueness theorems for the Riemann-Silberstein…
Electric Field Seen by an Observer

The Electric Field Seen by an Observer: A Relativistic Calculation with Tensors

/
0 Comments
This Insight was inspired by the discussion in "electric field seen by an observer in motion", which tries to understand the relation between two expressions:…
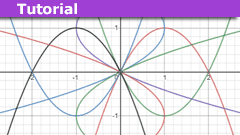
valentines reflections graphs

Valentine’s Reflections: Mathematical Matters of the Heart

/
4 Comments
Introduction Being a somewhat geeky Maths 'nerd', I spent days leading up to Valentine's Day trying to find a Maths function appropriate to the day. In…
electromagnetic computations

How to Use Duality in Computational Electromagnetic Problems

/
1 Comment
Some weeks ago I happened across a post that caught my eye. Dale asked a question about the number of photons in an electromagnetic field. His question…
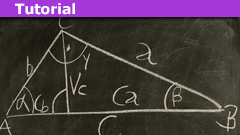
impossible triangles

Geometry of Side-side-angle (SSA) and Impossible Triangles

/
0 Comments
What is the ambiguous case? In high school geometry, the idea of proofs is often first introduced to American students. A common task is to use a basic…
equations of motion

Equations of Motion Revisited

/
1 Comment
Introduction In any school Physics course, the Newtonian equations of motion are very much a 'stock' item. Students learn the equations and are given…
Split Electric Fields

Split Electric Fields in Electrodynamics: Capacitor and Antenna

/
0 Comments
Abstract: The analysis of the two kinds of electric fields, namely the irrotational and non-conservative, is extended to electrodynamics, as exemplified…
projectile motion

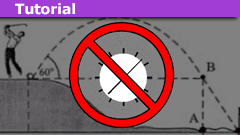
How to Master Projectile Motion Without Quadratics

/
6 Comments
Introduction In a homework thread a while back a PF member expressed dismay along the lines of "Oh no, not another boring projectile motion problem."…
strings waves

Intro to Physically Reasonable Waves on a String

/
4 Comments
Introduction Physics teachers who are either writing physics questions that deal with waves on a string or setting up equipment for a class lab or demo…
android ringtone

Create an Android Ringtone Picker with Ringtonemanager Class

/
3 Comments
In this article, I will show you how to create a ringtone picker using the RingtoneManager class in Android. You will be able to get the list of tones,…
artificial intelligence

How AI Is Changing STEM

/
0 Comments
We asked our PF Advisors “How do you see the rise in A.I. affecting STEM in the lab, classroom, industry and or in everyday society?”. We got so many…
calculus

How to Solve Second-Order Partial Derivatives

/
1 Comment
Introduction A frequent concern among students is how to carry out higher order partial derivatives where a change of variables and the chain rule are…
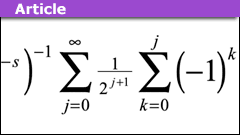
lerch and zeta functions

The Analytic Continuation of the Lerch and the Zeta Functions

/
0 Comments
Introduction In this brief Insight article the analytic continuations of the Lerch Transcendent and Riemann Zeta Functions are achieved via the Euler's…
Integral Representations of Some Special Functions

A Path to Fractional Integral Representations of Some Special Functions

/
9 Comments
Introduction This bit is what new thing you can learn reading this:) As for original content, I only have hope that the method of using the sets $$C_N^n:…
elastic ball collision

An Alternate Approach to Solving 2-Dimensional Elastic Collisions

/
4 Comments
Introduction This article follows on from the previous on an alternate approach to solving collision problems. In that article, we determined the equal…

How to Recognize Split Electric Fields

/
1 Comment
Introduction In a previous Insight, A New Interpretation of Dr. Walter Lewin’s Paradox, I introduced the fact that there are two kinds of E fields. …
Mass Generation

An Introduction to the Generation of Mass from Energy

/
28 Comments
Introduction This article is essentially an addition to the previous one on (mainly) inelastic collisions to include the particular case of inelastic…
Collision problems

An Alternative Approach to Solving Collision Problems

/
4 Comments
Introduction Collisions are very much a stock item in any school physics curriculum and students are generally taught about the use of the principles…
c++ guide for beginners

Guide to C++ Programming For Beginners

/
0 Comments
Contents 1. Getting a C++ Compiler and Compiling Your First Program 2. Simple Datatypes and Declarations 3. Operators and Expressions 4. Input and…
Odd Sums

Explore the Fascinating Sums of Odd Powers of 1/n

/
3 Comments
The goal is to get a little bit closer to the values of the zeta function (ζ(s)) and the eta function (η(s)) for some odd values of s. This insight is…
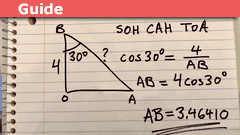
SOHCAHTOA

SOHCAHTOA: Seemingly Simple, Conceivably Complex

/
7 Comments
What is SOHCAHTOA SOHCAHTOA is a mnemonic acronym used in trigonometry to remember the relationships between the sides and angles of right triangles.…
recursion in programming

Recursion in Programming and When to Use or Not to Use It

/
38 Comments
Recursion is quite simple. It's a subroutine calling itself. It's surprising but some problems that look quite hard can be trivial using recursion - but…
maxwell magneto

Maxwell’s Equations in Magnetostatics and Solving with the Curl Operator

/
0 Comments
Introduction: Maxwell's equation in differential form ## \nabla \times \vec{B}=\mu_o \vec{J}_{total}+\mu_o \epsilon_o \dot{\vec{E}}  ##  with ## \dot{\vec{E}}=0…
Learn Dimensional Analysis

Learn the Basics of Dimensional Analysis

/
6 Comments
As a university teacher and as a PF member, I have often noted that students are largely unaware of or not using dimensional analysis to help them in their…
Quantum Mechanical Commutator

The Classical Limit of Quantum Mechanical Commutator

/
8 Comments
The Classical Limit of Commutator (without fancy mathematics) Quantum mechanics occupies a very unusual place among physical theories: It contains classical…
Minkowski Spacetime

Understanding Precession in Special and General Relativity

/
16 Comments
The Absolute Derivative In relativity we typically deal with two types of quantities: fields, which are defined everywhere, and particle properties, which…
isotropy definition

A Formal Definition of Large-Scale Isotropy

/
4 Comments
This Insight is part of my attempt to develop a formal definition of 'large-scale isotropy', a concept that is fundamental to most cosmology, but that…
surface integral

Demystifying Parameterization and Surface Integrals

/
3 Comments
Introduction This article will attempt to take the mystery out of setting up surface integrals. It will explain the basic ideas underlying surface integration…
Kerr Spacetime

Exploring Fermi-Walker Transport in Kerr Spacetime

/
2 Comments
In the last two posts in this series, we developed some tools for looking at Fermi-Walker transport in Minkowski spacetime and then applied them in Schwarzschild…
Minkowski_Spacetime_2

Learning Fermi-Walker Transport in Schwarzschild Spacetime

/
1 Comment
In the first post in this series, we introduced the concepts of frame field, Fermi-Walker transport, and the "Fermi derivative" of a frame field, and developed…
AVX-512 Programming subtotals

AVX-512 Programming: Extracting Column Subtotals from a Table

/
1 Comment
In this Insights article I'll present an example that shows how Intel® AVX-512 instructions can be used to read a whole row of data in a single operation,…
Minkowski Spacetime

Fermi-Walker Transport in Minkowski Spacetime

/
8 Comments
This is the first of several posts that will develop some mathematical machinery for studying Fermi-Walker transport. In this first post, we focus on Minkowski…
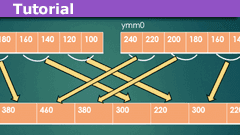
AVX-512 conclusion

AVX-512 Assembly Programming: Opmask Registers for Conditional Arithmetic Conclusion

/
1 Comment
In the first part of this article (AVX-512 Assembly Programing - Opmask Registers for Conditional Arithmetic), we looked at how opmask registers can be…
AVX-512 registers

AVX-512 Assembly Programming: Opmask Registers for Conditional Arithmetic

/
2 Comments
This is the second installment in a continuing series of articles on Intel AVX-512 assembly programming. The first installment is An Intro to AVX-512 Assembly…
AVX-512 Assembly Programming

An Intro to AVX-512 Assembly Programming

/
10 Comments
History In 1998, the Intel Corporation released processors that supported SIMD (single instruction, multiple data) instructions, enabling processors to…
Data Structures Programming

Intro to Data Structures for Programming

/
11 Comments
Introduction In the first part of this series, I talked about some fundamental notions in the world of algorithms. Beyond the definition of an algorithm,…
rotational mechanics

An Example of Servo-Constraints in Mechanics

/
4 Comments
Servo-constraint was invented by Henri Beghin in his Ph.D. thesis in 1922. For details see the celebrated monograph in rational mechanics by Paul Appell.To…
unity orbital mechanics

Orbital Mechanics in Unity Game Engine for Augmented Reality

/
2 Comments
In this Insight, I’ll go over implementing basic orbital mechanics simulations in the Unity game engine as well as an approach to scaling the simulation…
walter lewin

A New Interpretation of Dr. Walter Lewin’s Paradox

/
65 Comments
Much has lately been said regarding this paradox which first appeared in one of W. Lewin's MIT lecture series on ##{YouTube}^{(1)}##.  This lecture was…
Sagittarius A

How to Calculate the Spin of Black Hole Sagittarius A*

/
3 Comments
This Insight takes a look at how it is possible to calculate the spin of Sagittarius A*, the supermassive black hole at the center of the Milky Way using…
algorithms

Intro to Algorithms for Programming

/
28 Comments
Many threads here at PF include some questions about how to learn to program. This is asked by Physics students who want to learn programming to help their…
maxima

How to Solve Einstein’s Field Equations in Maxima

/
4 Comments
A few months ago, pervect pointed me to a post by Chris Hillman which is an introduction to the usage of Maxima for General Relativity. Maxima is a free…
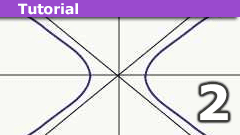
ridler_motion2

Rindler Motion in Special Relativity: Rindler Coordinates

/
27 Comments
Our destination In our last article, Hyperbolic Trajectories, we derived some facts about the trajectory of a rocket that is undergoing constant (proper)…
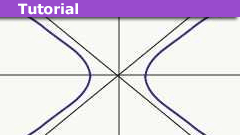
ridler_motion

Rindler Motion in Special Relativity: Hyperbolic Trajectories

/
5 Comments
Introduction: Why Rindler Motion? When students learn relativity, it's usually taught using inertial (constant velocity) motion. There are lots of reasons…
statmech1

Learn Statistical Mechanics: Equilibrium Systems

/
20 Comments
This is the first of a multi-part series of articles intended to give a concise overview of statistical mechanics and some of its applications. These articles…

Demystifying the Chain Rule in Calculus

/
7 Comments
Introduction There are a  number of posts on PF involving a general confusion over the multi-variable chain rule.  The problem is often caused by…
unitsworkforyou

How to Make Units of Measurement Work for You

/
13 Comments
How do we use units? You may see one of these speed limit signs, nearly every day. Even though neither of them displays units, drivers know they are implied.…
manifold2

A Journey to The Manifold SU(2): Representations

/
3 Comments
Part 1  Representations Image source: [23]  6. Some useful bases of ##\mathfrak{su}(2,\mathbb{C})## Notations can differ from author…
fourierseries2

Learn Further Sums Found Through Fourier Series

/
5 Comments
In an earlier insight, I looked at the Fourier series for some simple polynomials and what we could deduce from those series. There is a lot more to be…
Parsevalstheorem

Learn an Integral Result from Parseval’s Theorem

/
5 Comments
Introduction: In this Insight article,  Parseval's theorem will be applied to a sinusoidal signal that lasts a finite period of time.  It will be shown…
processing

The Joy of Processing

/
11 Comments
In the early days of the personal computer revolution, computers were small, simple, and easy to operate. It was always great fun to write BASIC games…
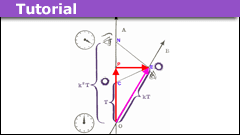
BondiKcalculus

Learn Relativity Using the Bondi K-calculus

/
20 Comments
Although Special Relativity was formulated by Einstein (1905), and given a spacetime interpretation by Minkowski (1908) [which helped make special relativity…
deriitive5

The Pantheon of Derivatives – Part V

/
2 Comments
  Important Theorems - biased, of course Implicit Function Theorem [1] Jacobi Matrix (Chain Rule). Let ## (x_0,y_0 ) ## be a point in$$U_1…
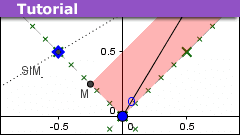
RelativityVariables

Relativity Variables: Velocity, Doppler-Bondi k, and Rapidity

/
8 Comments
Traditional presentations of special relativity place emphasis on "velocity", which of course has an important physical interpretation... carried over…
deriitive4

The Pantheon of Derivatives – Part IV

/
6 Comments
  Lie Derivatives A Lie derivative is in general the differentiation of a tensor field along a vector field. This allows several applications…
deriitive3

The Pantheon of Derivatives – Part III

/
3 Comments
  Some Topology Whereas the terminology of vector fields, trajectories, and flows almost by itself suggests its origins and physical relevance,…
deriitive2

The Pantheon of Derivatives – Part II

/
8 Comments
  Generalizations Beyond ##\mathbb{R}## and ##\mathbb{C}## As mentioned in the section on complex functions (The Pantheon of Derivatives - Part…
deriitive

The Pantheon of Derivatives – 5 Part Series

/
3 Comments
  Differentiation in a Nutshell I want to gather the various concepts in one place, to reveal the similarities between them, as they are often…
integraltrick

Trick to Solving Integrals Involving Tangent and Secant

/
6 Comments
This little trick is used for some integration problems involving trigonometric functions is probably well-known, but I only learned it yesterday. So…
linearacceleration

Frames of Reference: Linear Acceleration View

/
2 Comments
My previous Insight, Frames of Reference: A Skateboarder's View, explored mechanical energy conservation as seen from an inertial frame moving relative…
inferometer

Fabry-Perot and Michelson Interferometry: A Fundamental Approach

/
14 Comments
Fabry-Perot Effect: The Fabry-Perot effect is usually treated in most optics textbooks as the interference that results from multiple reflections of the…
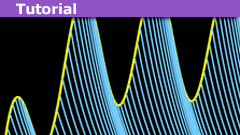
FourierSeries

Using the Fourier Series To Find Some Interesting Sums

/
4 Comments
Preliminaries If f(x) is periodic with period 2p and f’(x) exists and is finite for -π<x<π, then f can be written as a Fourier series: [itex]f(x)=\sum_{n=-\infty}^{\infty}a_{n}e^{inx}…
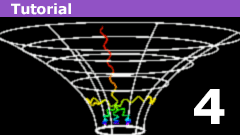
SchwarzschildGeometry4

The Schwarzschild Geometry: Physically Reasonable?

/
33 Comments
 In the last article, we looked at various counterintuitive features of the Schwarzschild spacetime geometry, as illustrated in the Kruskal-Szekeres…
SchwarzschildGeometry2

The Schwarzschild Geometry: Coordinates

/
2 Comments
 At the end of part 1, we looked at the form the metric of the Schwarzschild geometry takes in Gullstrand-Painleve coordinates:$$ ds^2…
SchwarzschildGeometry1

The Schwarzschild Geometry: Key Properties

/
22 Comments
 Not long after Einstein published his Field Equation, the first exact solution was found by Karl Schwarzschild. This solution is one of the…
partial-differentiation

Learn Partial Differentiation Without Tears

/
6 Comments
Differentiation is usually taught quite well. Perhaps that's because it is the first introduction to calculus, which is considered a big step in a student's…
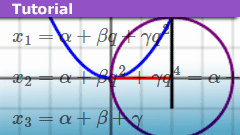
cubicfunction

Learn How to Solve the Cubic Equation for Dummies

/
5 Comments
Everybody learns the "quadratic formula" for solving equations of the form [itex]A x^2 + B x + C = 0[/itex], even though you don't really need such a formula,…
rollingmotion

Learn The Basics of Rolling Motion

/
50 Comments
Although rolling wheels are everywhere, when most people are asked "what is the axis of rotation of a wheel that rolls without slipping?", they will answer…
entropy

How to Determine the Change in Entropy

/
9 Comments
How do you determine the change in entropy for a closed system that is subjected to an irreversible process?Here are some typical questions we get…
Schwarzschild

Learn Orbital Precession in the Schwarzschild and Kerr Metrics

/
7 Comments
The Schwarzschild Metric A Lagrangian that can be used to describe geodesics is [itex]F = g_{\mu\nu}v^\mu v^\mu[/itex], where [itex]v^\mu = dx^\mu/ds[/itex]…
spacetimetetrad

Learn About Tetrad Fields and Spacetime

/
1 Comment
A spacetime is often described in terms of a tetrad field, that is, by giving a set of basis vectors at each point. Let the vectors of the tetrad be denoted…
omissionguage

Omissions in Mathematics Education: Gauge Integration

/
31 Comments
The current (pure) mathematics curriculum at the university is well-established. Most of the choices made are sensible. But still, some important topics…

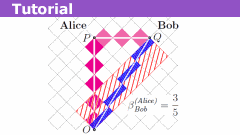
Learn About Relativity on Rotated Graph Paper

/
15 Comments
This Insight is a follow-up to my earlier tutorial Insight (Spacetime Diagrams of Light Clocks). I gave it a different name because I am placing more…